Mal wieder beginnt eine Prüfungsaufgabe mit einer Zeichnung. Für dich heißt das: Zurück in die 8. Klasse – Schrägbilder zeichnen wiederholen!
1. Zeichnen des Schrägbildes
Beispielaufgabe (Klapp mich aus)
1.0 Die Raute ABCD mit dem Mittelpunkt M ist die Grundfläche einer Pyramide mit Spitze S über dem Punkt M.
Es gilt: \( |\overline{AC}| = 10 cm; \\ |\overline{BD}| = 8 cm; |\overline{MS}| = 9 cm\).
Runden Sie im Folgenden auf zwei Stellen nach dem Komma.
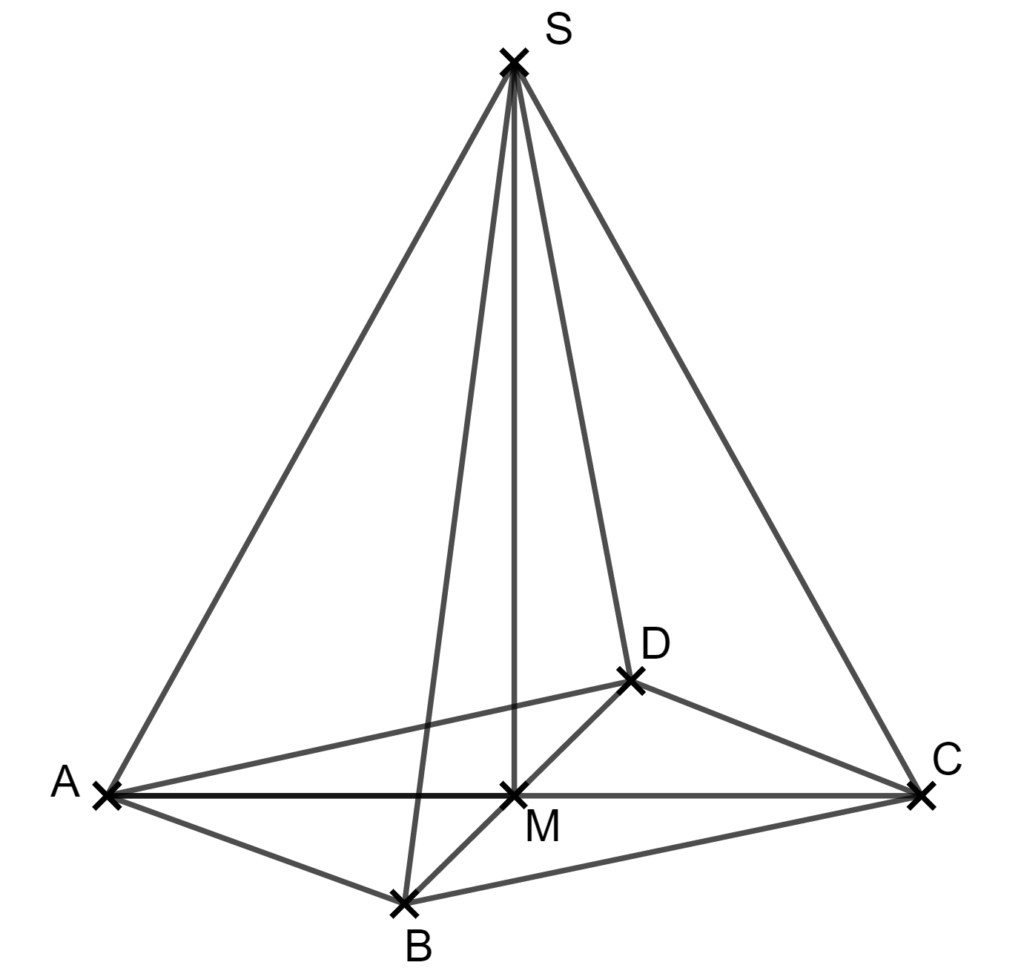
1.1 Zeichnen Sie ein Schrägbild der Pyramide ABCDS mit Schrägbildachse AC, wobei A links von C liegen soll.
Für die Zeichnung gilt: q = 0,5; ω = 45°
Am Anfang war das Grundwissen: Schrägbilder zeichnen! In allen MAPs bisher waren die Vorgaben gleich: q = 0,5, \(\omega\) = 45° . Alle verzerrten Strecken „in das Blatt hinein“ haben also die halbe Länge und bilden mit der Schrägbildachse einen 45°-Winkel. Oder anders gesagt: Es ist entlang der Kästchendiagonale.
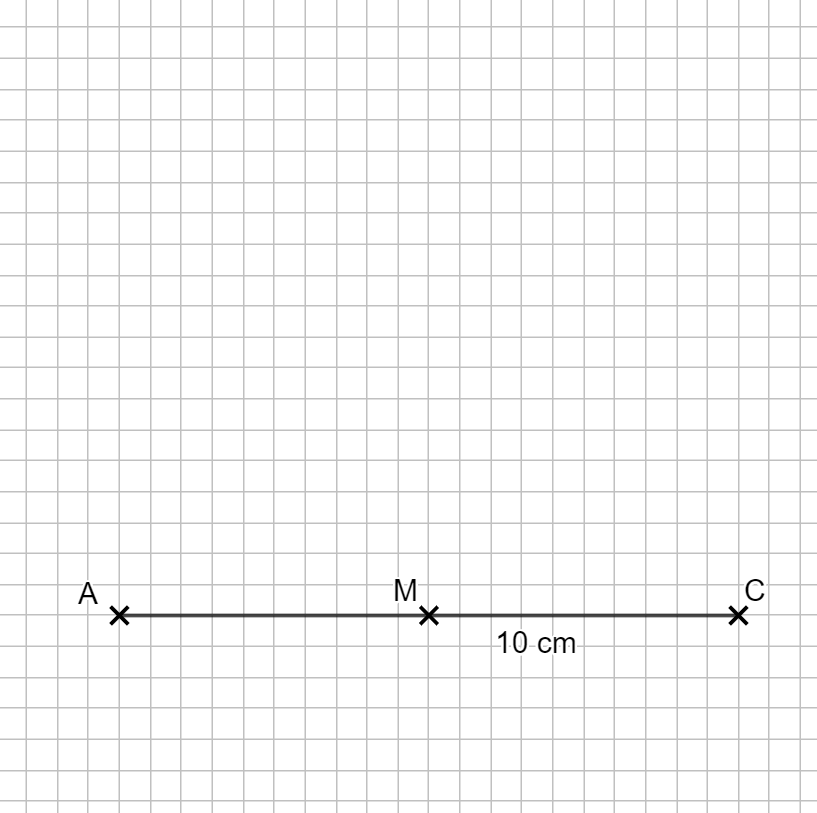
Beginne in der Mitte des Blattes und zeichne die Schrägbildachse zuerst! Der Punkt M soll der Mittelpunkt der Grundfläche sein und ist damit auch der Mittelpunkt der Strecke \( \overline{AC}\).
Die Diagonale \(\overline{BD}\) steht bei einer Raute senkrecht auf der anderen Diagonalen. Sie darf also in halber Länge als Kästchendiagonale gezeichnet werden.
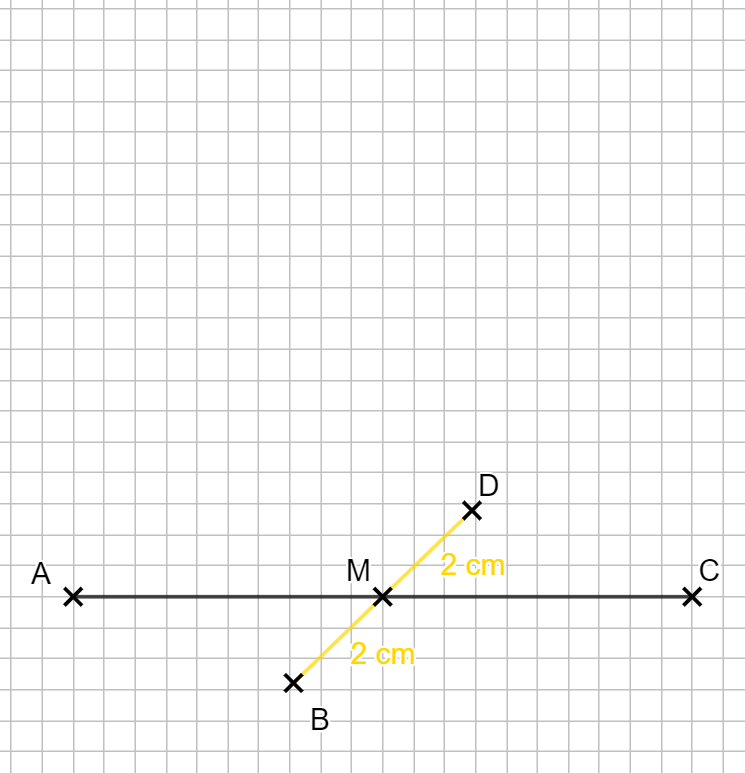
In wahrer Größer ist die Strecke \(|\overline{BD}| = 8cm\) lang, in der Zeichnung also 4 cm. Damit muss von M aus 2 cm nach hinten und 2 cm nach vorne gezeichnet werden und du landest knapp vor einem Kästchenkreuz.
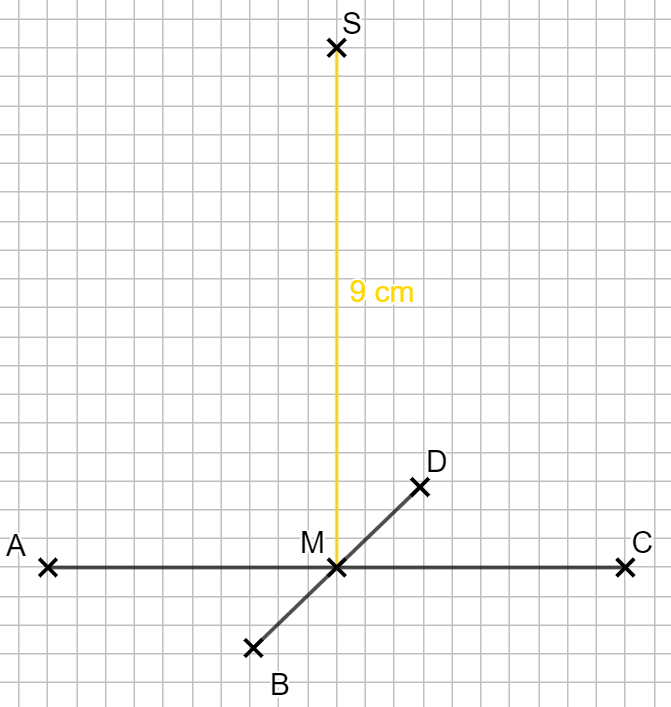
Die Spitze S soll 9 cm über dem Mittelpunkt M liegen. Die Höhe darf hier in wahrer Größe eingezeichnet werden.
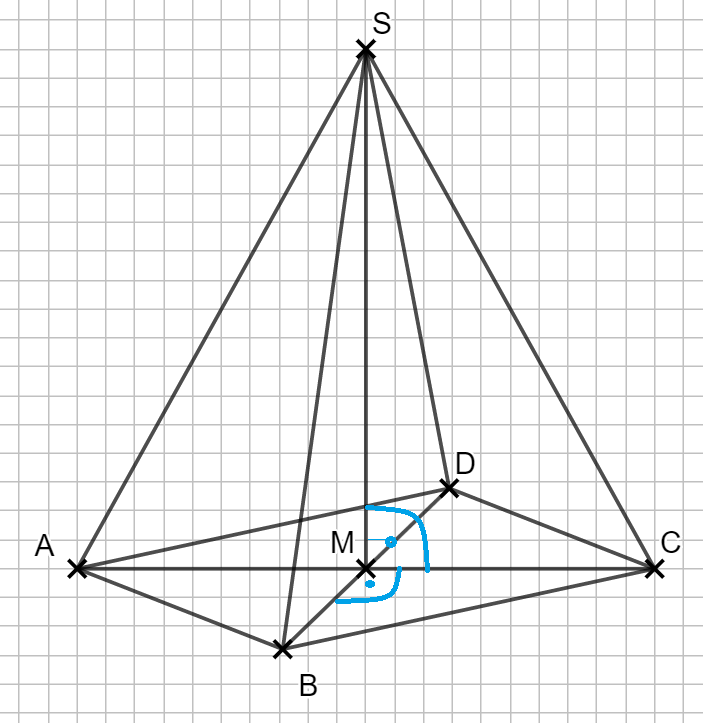
Zu guter Letzt verbindest du die Punkt zum gesuchten Körper. Ich empfehle dir an dieser Stelle die verzerrten rechten Winkel einzutragen, dann vergisst du sie später nicht!
In der Abschlussprüfung gibt es auch immer eine Skizze. Natürlich nimmst du diese am Ende, um nochmal die Namen der Punkte zu vergleichen und mit Augenmaß zu prüfen, ob das so stimmt.
Dann sind die ersten Punkte in der Raumgeometrie geschafft!
Schritt für Schritt
- Beginne mit der Schrägbildachse!
- Zeichne senkrechte Strecken auf die Schrägbildachse mit halber Länge als Kästchendiagonale!
- Ergänze den Körper über seine Eigenschaften.
- (Markiere rechte Winkel für später)
Jetzt bist du dran
Übung 1
1.0 Die nebenstehende Skizze zeigt ein Schrägbild der Pyramide ABCDS, deren Grundfläche die Raute ABCD mit dem Diagonalenschnittpunkt M ist.
Die Spitze S der Pyramide ABCDS liegt senkrecht über dem Mittelpunkt M.
Es gilt:
\( |\overline{AC}| = 12 cm; |\overline{BD}|= 8 cm; |\overline{MS}| = 9 cm \)
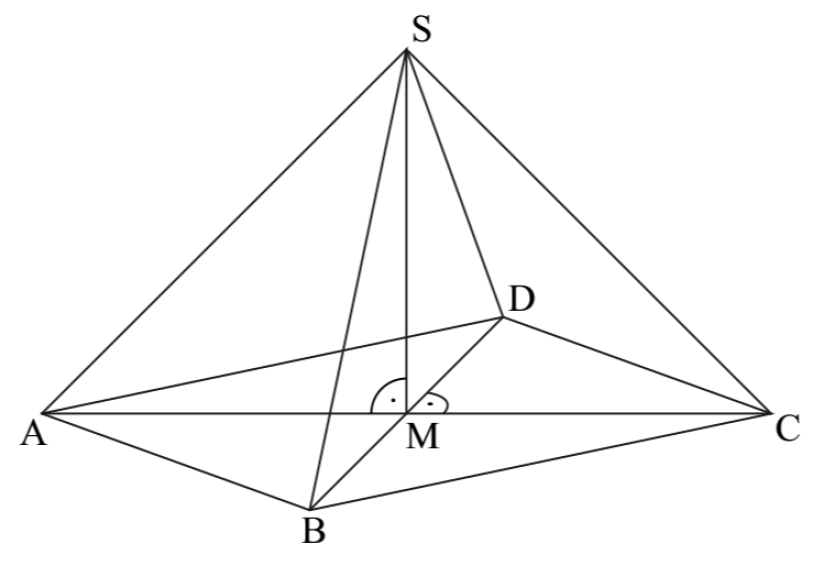
Runden Sie im Folgenden auf zwei Stellen nach dem Komma.
1.1 Zeichnen Sie das Schrägbild der Pyramide ABCDS, wobei die Strecke \(\overline{AC]\) auf der Schrägbildachse und der Punkt A links von Punkt C liegen soll.
Für die Zeichnung gilt: q = 0,5 ; ω = 45°.
Lösung zu Übung 1.1
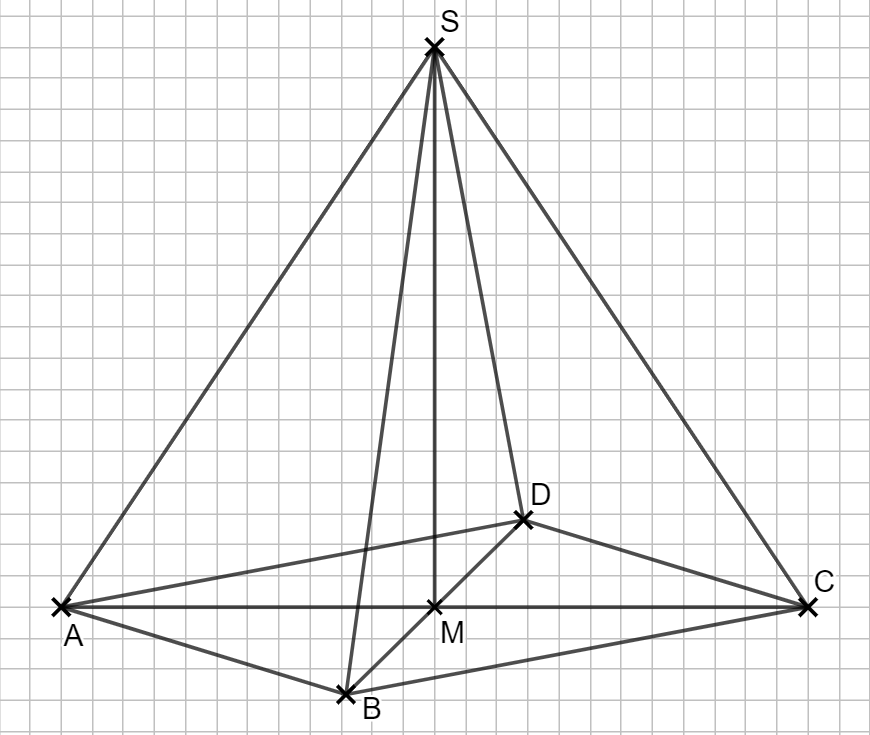
Übung 2
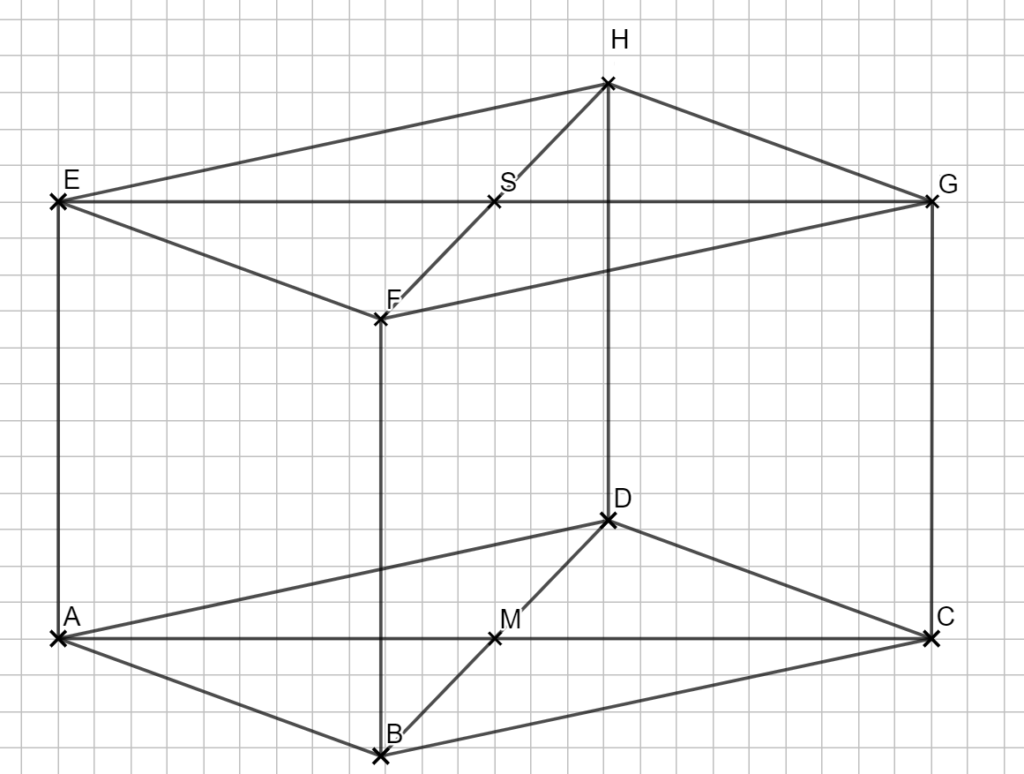
2.0 Die nebenstehende Skizze zeigt ein Schrägbild des geraden Prismas ABCDEFGH, deren Grundfläche eine Raute ABCD mit Mittelpunkt ist. Die Punkte E, F, G und H liegen jeweils senkrecht über der Punkten A, B, C und D und bilden Rauten EFGH mit Mittelpunkt S
Es gilt:
\( |\overline{AM}| = 6 cm; |\overline{BD}|= 9 cm ; |\overline{AE}| = 6 cm \)
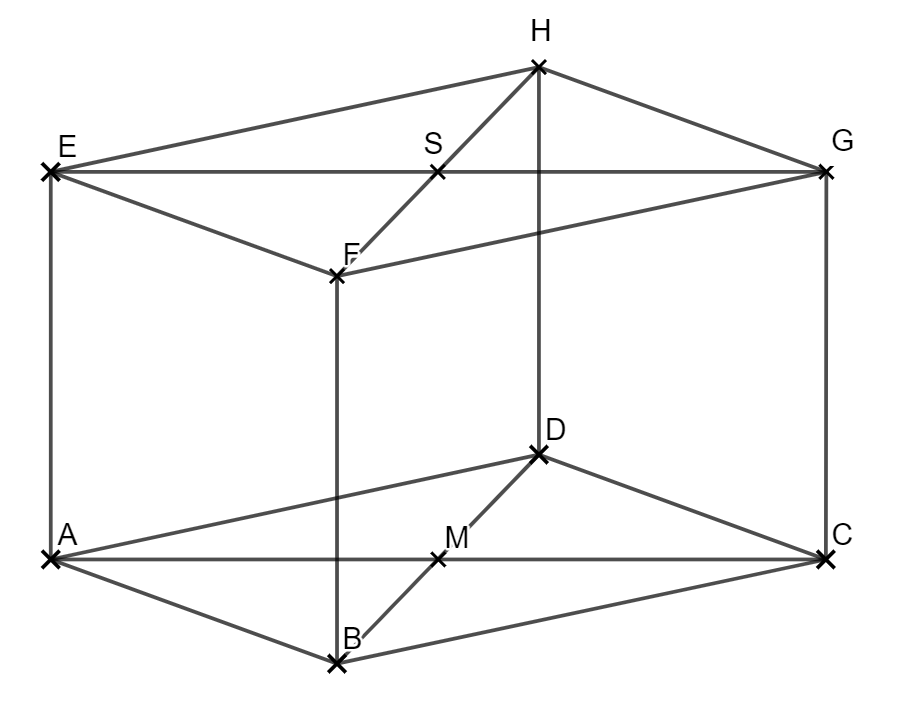
Runden Sie im Folgenden auf zwei Stellen nach dem Komma.
2.1 Zeichnen Sie das Schrägbild der Pyramiden ABCDEFGH, wobei die Strecke \( \overline{AC}\) auf der Schrägbildachse und der Punkte A links vom Punkt C liegen soll.
Für die Zeichnung gilt: q = 0,5 ; ω = 45°.
Lösung zu Übung 2.1
MAPS zum Üben
| 2021 | 2020 | 2019 | 2018 | 2017 | 2016 | 2015 | 2014 | |
| Haupttermin | B2.1 | B2.1 | B2.1 | B2.1 | B2.1 | B2.1 | ||
| Nachtermin | B2.1 | B2.1 | B2.1 | B2.1 | B2.1 | B2.1 |
Auf geht es zum nächsten Kapitel
Jeder MAP-Hack hat den gleichen Aufbau, den du auch im Probekapitel kennenlernen durftest. Anhand einer Beispielaufgabe wird der Aufgabentyp und die Bearbeitung erklärt. Die Schritt-für-Schritt-Anleitung fasst allgemein zusammen und hilft dir, die beiden Übungsaufgaben zu bearbeiten. Wenn dir die beiden Übungen noch nicht reichen, kannst du alle Prüfungen der letzten Jahre machen. Also mehr als genug Übungsmaterial für eine super Prüfungsvorbereitung.
Schau im Shop vorbei und bereite dich mit dem MAP-Hack auf die wichtigste Mathe-Prüfung vor!
