

Lösung zu 2.1
Die Höhe steht immer senkrecht, du darfst also Sin/Cos/Tan und den SdP verwenden.
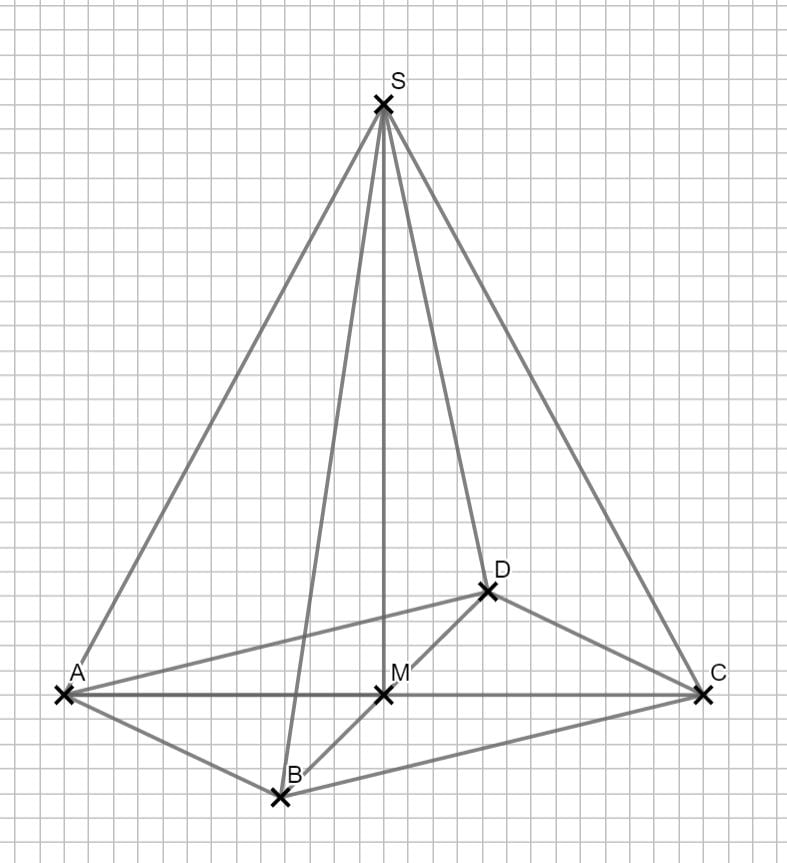
\begin{align} & |\overline{CS}| \text{ mit dem Satz des Pythagoras:} \\
|\overline{CS}|^2 &= |\overline{AM}|^2 + |\overline{MS}|^2 \\
&= (0,5 \cdot 13)^2 + 12^2 \\
\Rightarrow &|\overline{AM}| = 13,65 cm \\
\\
& \angle SCA \text{ mit dem Tangens:} \\
tan(\angle SCA) &= \frac{|\overline{MS}|}{|\overline{AM}|} \\
&= \frac{12}{0,5 \cdot 13} \\
\Rightarrow & \angle SCA = 61,56° \end{align}
Zurück zum MAP-Hack:

Lösung zu 2.2
Hinten das Lesen anfangen. x = 3 und jetzt Schritt-für-Schritt!
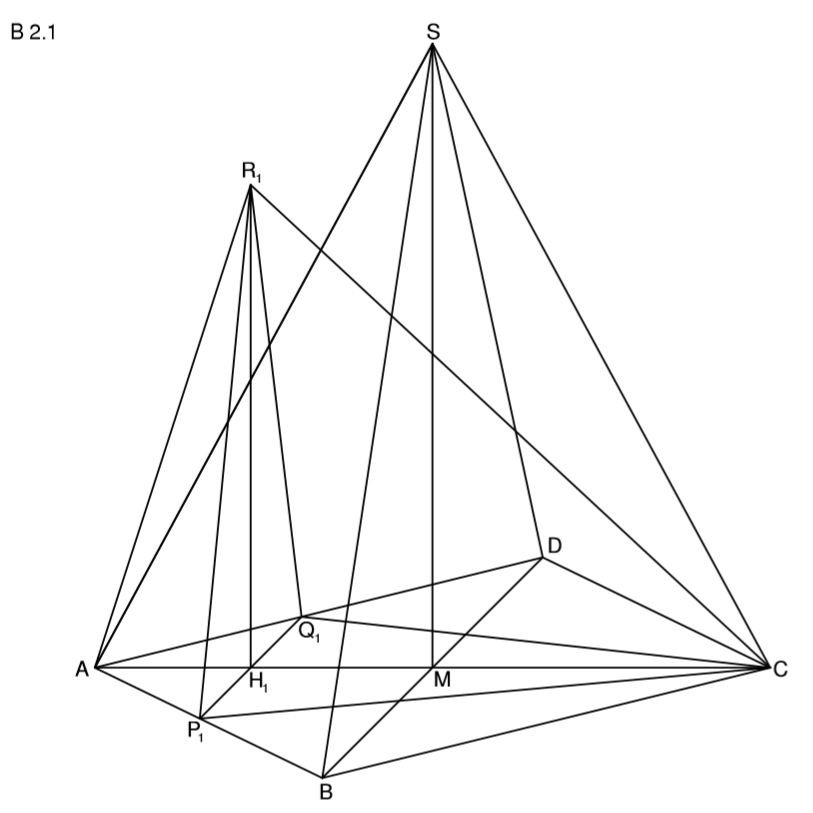
Zurück zum MAP-Hack:

Lösung zu 2.3
Die Aufgabe besteht aus drei Schritten: Berechnung des Volumens der kleinen Pyramide, Berechnung des Volumens der großen Pyramide und der Bestimmung des prozentualen Anteils. Um das kleinere Volumen zu bestimmen, benötigst du die Längen der Diagonalen.
\begin{align} &V_{klein} \text{ mit } |\overline{P_1 Q_1}| \text{ und } |\overline{H_1 R_1}|: \\
\\
& |\overline{P_1 Q_1}| \text{ mit dem Vierstreckensatz:} \\
\frac{|\overline{P_1 Q_1}|}{|\overline{BD}|} &= \frac{x}{|\overline{AM}|} \\
\frac{|\overline{P_1 Q_1}|}{12} &= \frac{3}{0,5 \cdot 13} \,\,\, | \cdot 12 \\
|\overline{P_1 Q_1}| &= \frac{3}{6,5} \cdot 12 \\
\Rightarrow &|\overline{P_1 Q_1}| = 5,54 cm \\
\\
& |\overline{H_1 R_1}| \text{ mit dem Satz des Pythagoras:} \\
|\overline{CS}|^2 &= (|\overline{AC}| – x)^2 + |\overline{H_1 R_1}|^2 \\
|\overline{H_1 R_1}|^2 &= |\overline{CS}|^2- (|\overline{AC}| – x)^2 \\
&=(13,65)^2 -(13 – 3)^2 \\
\Rightarrow &|\overline{H_1 R_1}| = 9,29 cm \\
\\
&\text{Berechnung des Volumens } V_{klein}: \\
V_{klein} &= \frac{1}{3} \cdot \frac{1}{2} \cdot |\overline{AC}| \cdot |\overline{P_1 Q_1}| \cdot |\overline{H_1 R_1}| \\
&= \frac{1}{3} \cdot \frac{1}{2} \cdot 13 \cdot 5,54 \cdot 9,29 \\
\Rightarrow & V_{klein} = 111,51 cm^3 \\
\\
&\text{ Berechnung von }V_{groß}: \\
V_{groß} &= \frac{1}{3} \cdot \frac{1}{2} \cdot |\overline{AC}| \cdot |\overline{BD}| \cdot |\overline{MS}| \\
&= \frac{1}{3} \cdot \frac{1}{2} \cdot 13 \cdot 12 \cdot 12 \\
\Rightarrow &V_{groß} = 312 cm^3 \\
\\
&\text{Berechnung des Prozentsatzes: }\\
p &= \frac{V_{klein}}{V_{groß}} \cdot 100 \% \\
&= \frac{111,51}{312} \cdot 100 \% \\
\Rightarrow &p = 35,74 \% \end{align}
Zurück zum MAP-Hack:

Lösung zu 2.4
Im rechtwinkligen Dreieck darfst du Sin/Cos/Tan und SdP verwenden.
\begin{align} & |\overline{CH_2}| \text{ mit dem Satz des Pythagoras:} \\
|\overline{CS}|^2 &= |\overline{CH_2}|^2 + |\overline{H_2 R_2}|^2 \\
|\overline{CH_2}|^2 &= |\overline{CS}|^2 – |\overline{H_2 R_2}|^2 \\
&= 13,65^2 – 6^2 \\ \Rightarrow &|\overline{CH_2}| = 12,26 \\
|\overline{AH_2}| &= 13 – 12,26 = 0,74 cm. \end{align}
Es gilt: x = 0,74.

Lösung zu 2.5
Setze in den Satz des Pythagoras die Terme und Zahlen ein, die du aus den Aufgaben vorher kennst. Löse die Quadrate auf und ziehe ganz am Ende die Wurzel asu dem Term, indem du sie einfach über alles darüber schreibst.
\begin{align} &|\overline{H_N R_N}| \text{ mit dem Satz des Pythagoras:}
\\ |\overline{H_N R_N}| &= |\overline{CS}|^2 – (|\overline{AC}| – x)^2 \\ &= 13,65^2 – (13 – x) ^2 \\
&= 13,65^2 – (169 – 26x + x^2) \\
&= -x^2 + 26x + 17,32 \\
\Rightarrow |\overline{H_n R_n}| &= \sqrt{-x^2 + 26x + 17,32} cm \end{align}

Lösung zu 2.6
Fange mit RCA = 15° an und berechne etwas, an dem du begründen kannst, dass das nicht sein kann.
Angenommen es gibt eine Pyramide, in der es den Winkel RCA = 15° gibt, dann können wir mit \( \overline{CS} \) den Cosinus ansetzen:
\begin{align} cos(\angle RCA) &= \frac{\overline{CH_3}}{\overline{CS}} \, \, | \cdot \overline{CS} \\ \overline{CH_3} &= cos(15°) \cdot 13,65 = 13,18. \\ \overline{CH_3} = 13,18 &> \overline{AC} \end{align}
Damit liegt aber H nicht mehr auf [AM], was nicht sein darf.

Du hast eine Frage zu einer Teilaufgabe oder zur Lösung? Schreib’ hier und du bekommst eine Antwort!