2016 Haupttermin B2: Raumgeometrie

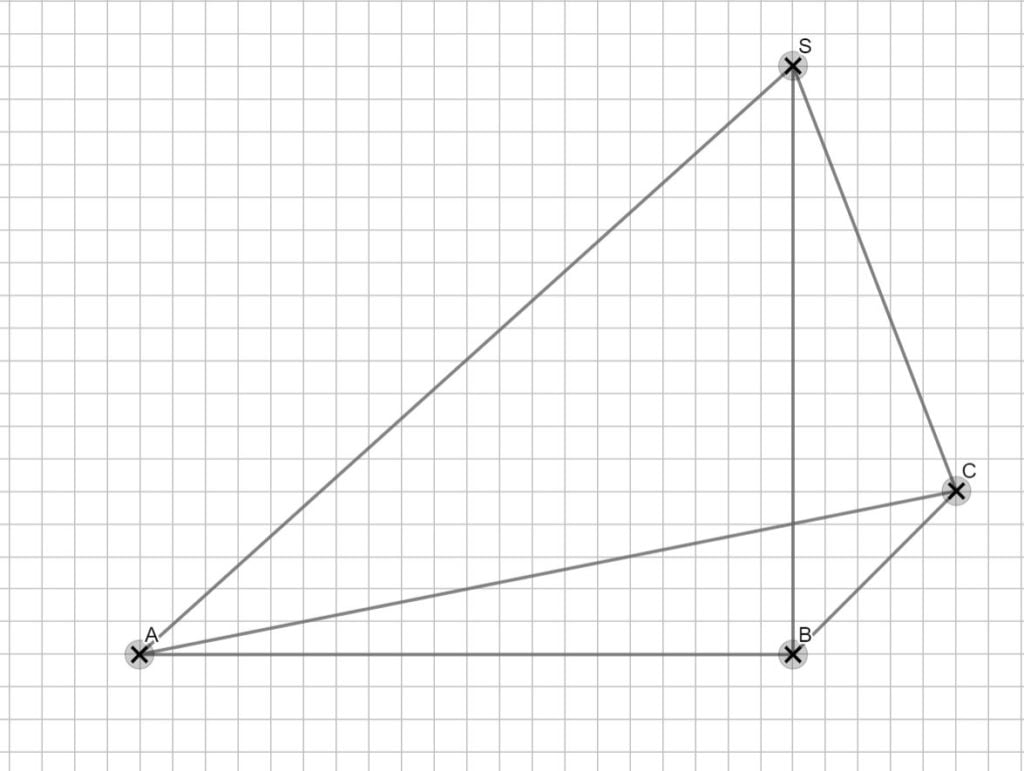
\begin{align} &\overline{CS} \text{ mit dem Satz des Pythagoras:} \\
\overline{CS}^2 &= \overline{AC}^2 + \overline{AS}^2 \\
\overline{CS}^2 &= 10^2 + 9^2 \\
\Rightarrow &\overline{CS} = 13,45 cm \\
\\
&\varepsilon \text{ mit dem Tangens:}\\
tan(\varepsilon) &=\frac{\, \overline{AS} \,}{\overline{AC}} \\
&= \frac{\, 9 \,}{10} \\
\Rightarrow &\varepsilon = 41,99° \end{align}

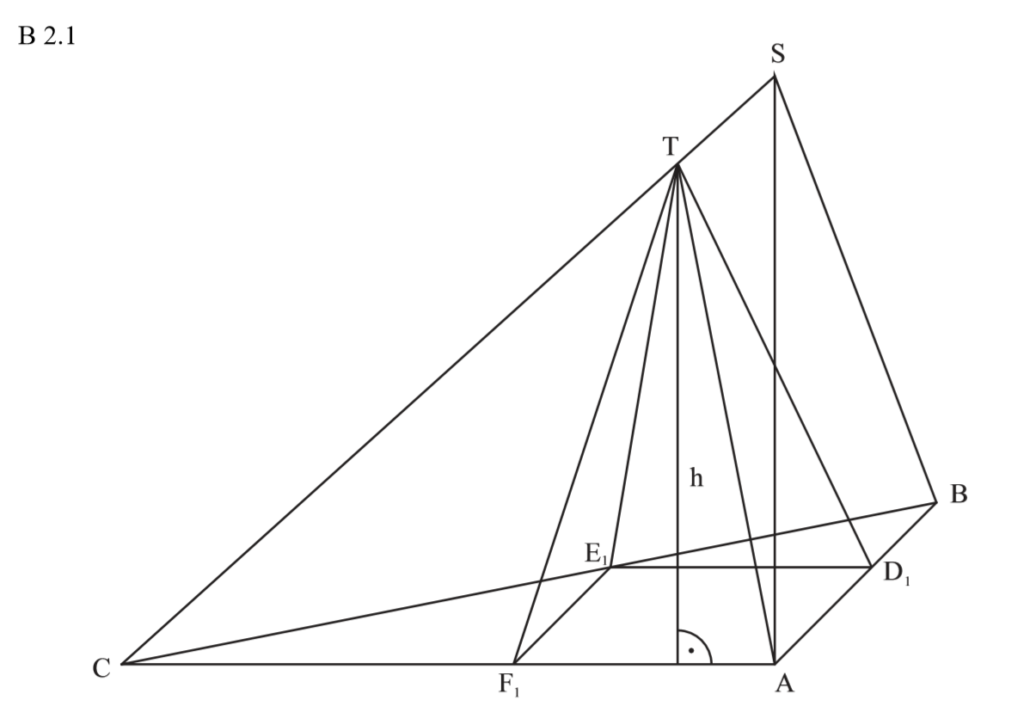
\begin{align} &\overline{ E_n F_n} \text{ mit dem Vierstreckensatz:}\\
\frac{\, \overline{E_n F_n} \,} {\overline{AB}} &= \frac{ \, \overline{CF_n} \,}{\overline{AC}} \\
\frac{\, \overline{E_n F_n} \,}{7} &= \frac{\, 10 \, – \, x\,}{10} \,\,\, |\cdot 7\\
\Rightarrow &\overline{E_n F_n} = (-0,7x + 7) cm \end{align}

In einem Quadrat haben alle Seiten gleiche Länge. Damit lässt sich eine Gleichung aufstellen und lösen:

\begin{align} \overline{AF} &= \overline{EF} \\
x &= -0,7x + 7 \,\,\, |+0,7x \\
1,7x &= 7 \,\,\, |:1,7 \\
\Rightarrow x &= 4,12 \end{align}

\begin{align} &\text{Einsetzen in die Flächenformel:} \\
A(x) &= \overline{AF_n} \cdot \overline{E_n F_n} \\
&= x \cdot (-0,7x + 7) \\
\Rightarrow &A(x) = (-0,7x^2 + 7x) cm^2 \\
\\
&\text{Berechnung des Extremwerts mit dem GTR:}\\
\Rightarrow &\text{GTR: } A_{max} = 17,5 \, für \, x=5 \end{align}

\begin{align} &h \text{ mit dem Sinus }: \\
sin(\varepsilon) &= \frac{ h } {\, \overline{CT} \, } \,\,\, |\cdot \overline{CT} \\
h &= sin(\varepsilon) \cdot \overline{CT} \\
&= sin(\varepsilon) \cdot (\overline{CS} – \overline{TS})\\
&= sin(41,99°) \cdot (13,45 – 2) \\
\Rightarrow &h = 7,66 cm \end{align}

\begin{align} &\alpha < 138,01° \text{ mit der Innenwinkelsumme:} \\
\alpha + \varepsilon &< 180° \\
\alpha + 41,99° &< 180° \,\,\, | -41,99° \\
\alpha &< 138,01° \end{align}

Um die untere Intervallgrenze zu bestimmen, berechnest du \( \overline{AT} \) mit dem Cosinussatz, um dann mit dem Sinus auf den Winkel TAC zu schließen. Du berechnest als oden kleinesten möglichen Winkel über ein Hilfsdreieck:

\begin{align} &\overline{AT} \text{ mit dem Cosinussatz:}\\
\overline{AT}^2 &= \overline{AC}^2 + \overline{CT}^2 – 2 \cdot \overline{AC} \cdot \overline{CT}^2 \cdot cos(\varepsilon) \\
&= 10^2 + 11,45^2 – 2 \cdot 10 \cdot 11,45 \cdot cos(41,99°) \\
\Rightarrow &\overline{AT} = 7,80 \\
\\
&\angle TAC \text{ mit dem Sinus:}\\
sin(\angle TAC) &= \frac{\, h \, }{\, \overline{AT} \,} \\
&= \frac{\, 7,66 \,}{7,80} \\
\Rightarrow &\angle TAC = 79,13° \end{align}