

Lösung zu B2.1
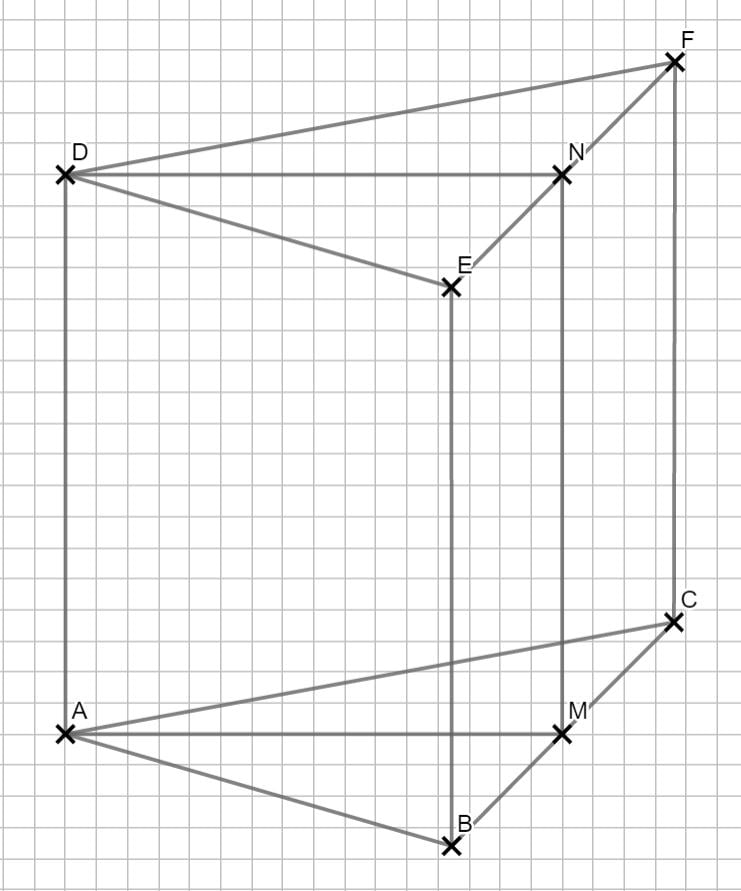
\begin{align} & \frac{\varphi}{2} \, im \, Dreieck \, ABM: \\ tan(\frac{\varphi}{2}) &= \frac{0,5 \cdot \overline{BC}}{overline{AM}} \\ &= \frac{0,5 \cdot 10}{8} \\ \frac{\varphi}{2} &= 32,005° \\ \Rightarrow &\varphi = 64,01° \end{align}
Zurück zum MAP-Hack:

Lösung zu B2.2
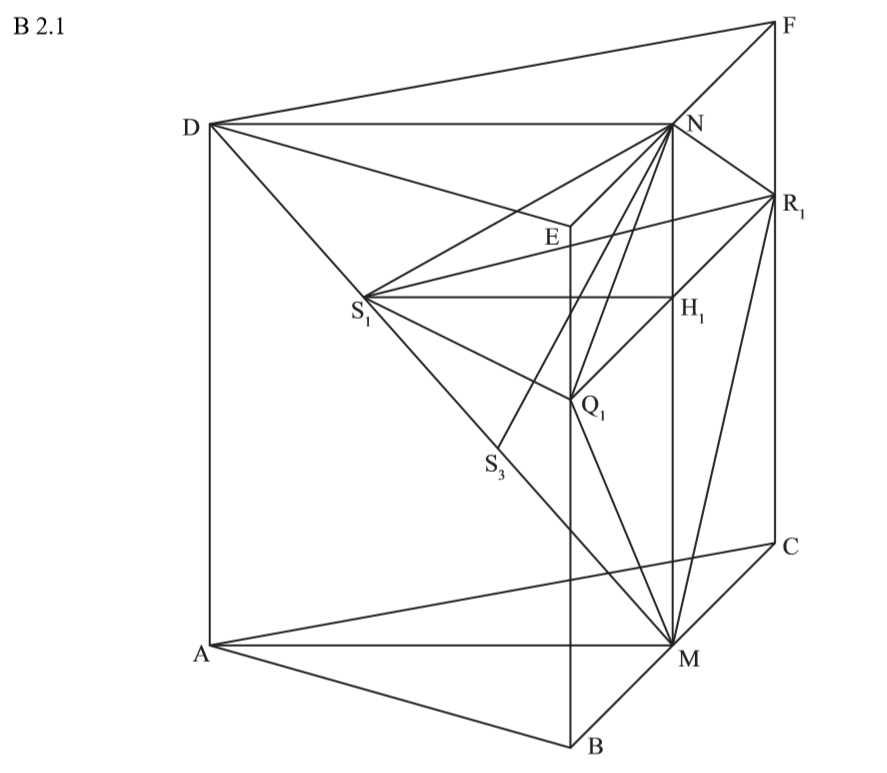
\begin{align} & \overline{MD} \, mit \, dem \, Satz \, des \, Pythagoras: \\ \overline{MD} &= \overline{AM}^2 + \overline{AD}^2 \\ &= 8^2 + 9^2 \\ \Rightarrow &\overline{MD} = 12,04 cm \\ \\ &\epsilon \, mit \, dem \, Tangens: \\ tan(\epsilon) &= \frac{\overline{AM}}{\overline{AD}} \\ &= \frac{8}{9} \\ \Rightarrow &\epsilon = 41,63° \end{align}
Zurück zum MAP-Hack:

Lösung zu B2.3
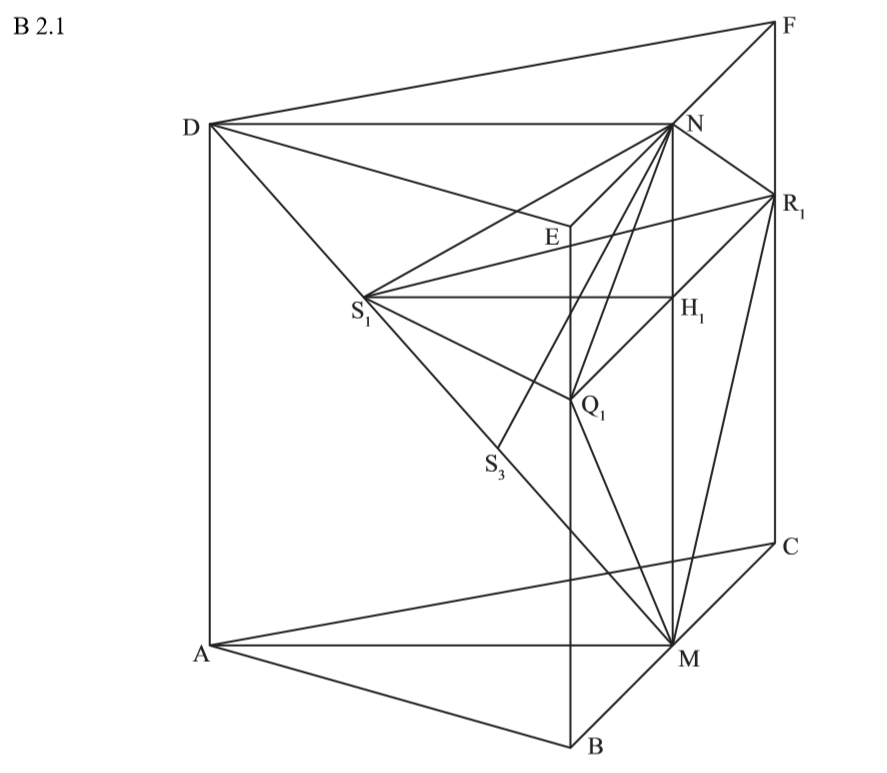
\begin{align} &\overline{S_1 H_1} \, mit \, dem \, Sinus: \\sin(\epsilon) &= \frac{\overline{S_1 H_1}}{\overline{MD} – x} \\ sin(41,63°) &= \frac{\overline{S_1 H_1}}{12,04 – 4} \,\,\, |\cdot 8,04 \\ \overline{S_1 H_1} &= sin(41,63°) \cdot 8,04 \\ \Rightarrow &\overline{S_1 H_1} = 5,34 cm \end{align}

Lösung zu 2.4
Um in die Volumenformel für die Pyramide einsetzen zu können, benötigst du die Höhe \( h = \overline{S_n H_n} \). Du kannst sie in mit dem Vierstreckensetz berechnen:
\begin{align} &\overline{S_n H_n} \, mit \, dem \, Vierstreckensatz: \\ \frac{\overline{S_n H_n}}{\overline{DN}} &= \frac{\overline{MD}-x}{MD} \\ \frac{\overline{S_n H_n}}{8} &= \frac{12,04 -x}{12,04} \,\,\ |\cdot 8 \\ \overline{S_n H_n}&= \frac{12,04 -x}{12,04} \cdot 8 \\ \overline{S_n H_n} &= 8 – 0,66x \\ \\ &Einsetzen \, in \, die \, Volumenformel: \\ V(x) &= \frac{1}{3} \cdot A_G \cdot h \\ &= \frac{1}{3} \cdot \frac{1}{2} \cdot \overline{MN} \cdot \overline{Q_n R_n} \cdot \overline{S_n H_n} \\ &= \frac{1}{3} \cdot \frac{1}{2} \cdot 9 \cdot 10 \cdot (8-0,66x) \\ \Rightarrow &V(x) = (120 – 9,9 x) cm^3 \end{align}
Zurück zum MAP-Hack:
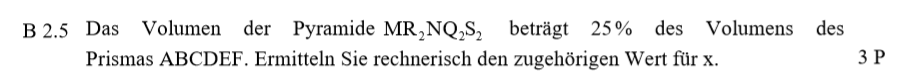
Lösung zu B2.5
\begin{align} &V_{Prisma} \, mit \, der \, Prisma-Formel: \\ V_{Prisma} &= A_G \cdot h \\ &= 0,5 \cdot \overline{AM} \cdot \overline{BC} \cdot \overline{MN} \\ &= 0,5 \cdot 10 \cdot 8 \cdot 9 \\ \Rightarrow &V_{Prisma} = 360 cm^3 \\ \\ &Berechnung \, von \, x : \\ 0,25 \cdot V_{Prisma} &= V(x) \\ 0,25 \cdot 360 &= 120 – 9,9x \,\,\, |- 120 |:(-9,9) \\ \Rightarrow &x= 3,03 \end{align}
Zurück zum MAP-Hack:

Lösung zu B2.6
\begin{align} & \angle S_3NM \, die \, Innenwinkelsumme: \\ \angle S_3NM &= 180° – \angle MS_3N – \angle NMS_3 \\ &= 180° – 110° – 41,63° \\Rightarrow &\angle S_3NM = 28,37° \\ \\ &x \, mit \, dem \, Sinussatz: \\ \frac{\overline{MS_3}}{sin(\angle S_3NM} &= \frac{\overline{MN}}{sin(\angle MS_3N)} \\ \frac{12,04 -x}{sin(28,37°)} &= \frac{9}{sin(110°)} \,\,\, |\cdot sin(28,37°) \\ 12,04 – x &= \frac{9}{sin(110°)} \cdot sin(28,37°) \,\,\, |-12,04 |\cdot (-1) \\ x &= \frac{9}{sin(110°)} \cdot sin(27,37°) \cdot (-1) \\ \Rightarrow &x = 7,49 \end{align}

Du hast eine Frage zu einer Teilaufgabe oder zur Lösung? Schreib‘ hier und du bekommst eine Antwort!