

Lösung zu B2.1
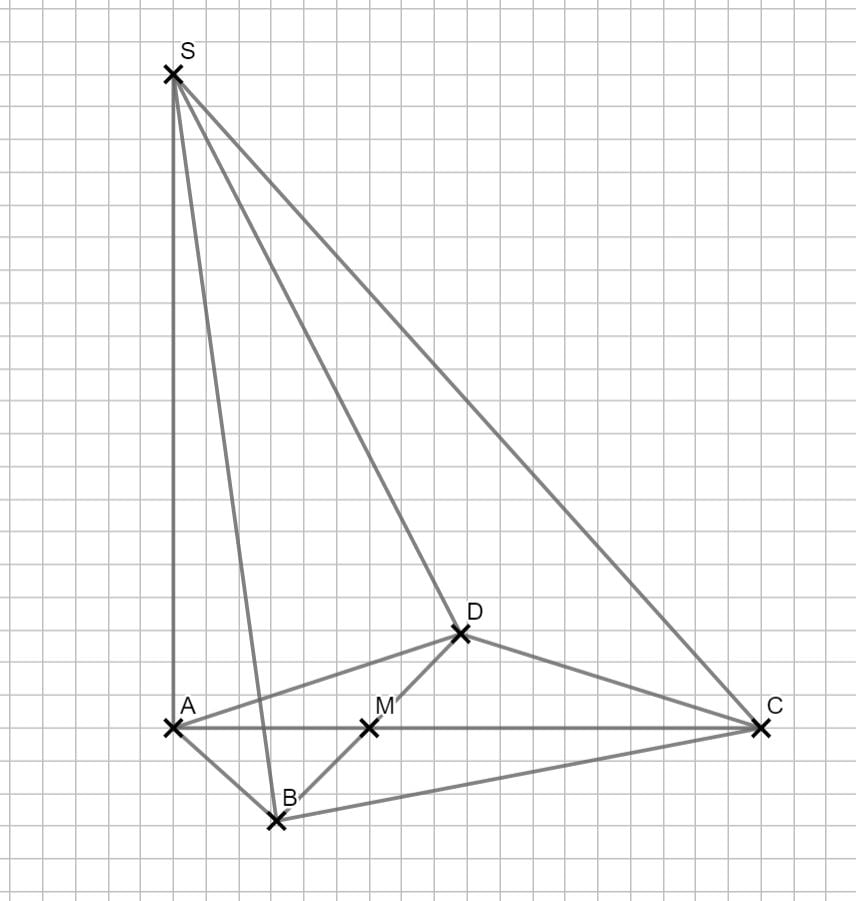
\begin{align} & \overline{MS} \, mit \, dem \, Satz \, des \, Pythagoras: \\ \overline{MS}^2 &= \overline{AS} ^2 + \overline{AM}^2 \\ &= 10^2 + 3^2 \\ \Rightarrow & \overline{MS} = 10,44 cm \\ \\ & \varphi \, mit \, dem \, Tangens: \\ tan(\varphi) &= \frac{\overline{AS}}{\overline{AM}} \\ &= \frac{10}{3} \\ \Rightarrow &\varphi = 73,30° \end{align}
Phi kannst du auch mit dem Sinus oder dem Cosinus berechnen.
Zurück zum MAP-Hack:

Lösung zu B2.2

Zurück zum MAP-Hack:
Lösung zu B2.3
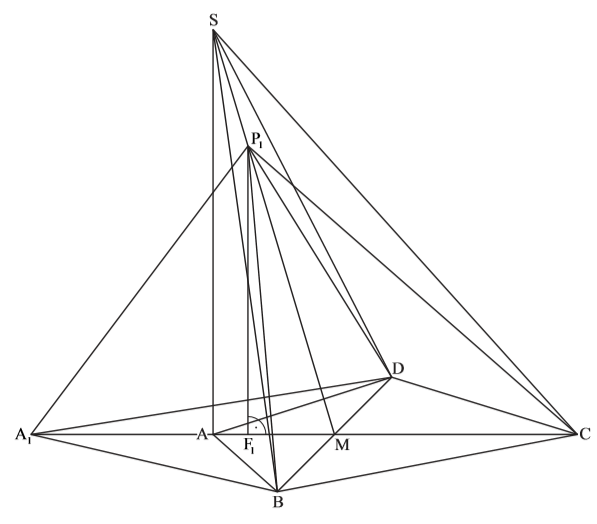
\begin{align} &\overline{A_1 P_1} \, mit \, dem \, Cosinussatz: \\ \overline{A_1 P_1}^2 &= \overline{A_1 M}^2 + \overline{MP_1}^2 – 2 \cdot \overline{A_1 M} \cdot \overline{MP_1} \cdot cos(\varphi) \\ &= 7,5^2 + 7,44^2 – 2 \cdot 7,5 \cdot 7,44 \cdot cos(73,3°) \\ \Rightarrow &\overline{A_1 P_1} = 8,92 cm \\ \\ &\alpha \, mit \, dem \, Sinussatz: \\ \frac{sin(\alpha)}{\overline{MP_1}} &= \frac{sin(\varphi)}{\overline{A_1 P_1}} \,\,\, |\cdot \overline{MP_1} \\ &= \frac{sin(\varphi)}{\overline{A_1 P_1}} \cdot \overline{M_1 P_1} \\ &= \frac{sin(73,30°)}{8,92} \cdot 7,44 \\ \Rightarrow &\alpha = 53,03° \end{align}
Lösung zu B2.4
Um das funktionale Volumen zu bestimmen, benötigst du die Höhe [PF] in Abhänigkeit von x:
\begin{align} &\overline{P_n F_n} \, mit \, dem \, Vierstreckensatz: \\ \frac{\overline{P_n F_n}}{\overline{AS}} &= \frac{\overline{MP_n}}{\overline{MS}} \, \, \, |\cdot \overline{AS} \\ \overline{P_n F_n} &= \frac{\overline{MP_n}}{\overline{MS}} \cdot \overline{AS} \\ &= \frac{10,44 -x } {10,44} \cdot 10 \\ \Rightarrow &\overline{P_n F_n} = (10 – 0,96x) cm \\ \\ & Einsetzen \, in \, die \, Volumenformel: \\ V_{Pyramide} &= \frac{1}{3} \cdot A_g \cdot h \\ &= \frac{1}{3} \cdot \frac{1}{2} \cdot \overline{A_n C} \cdot \overline{BD} \cdot \overline{P_n F_n} \\ &= \frac{1}{3} \cdot \frac{1}{2} \cdot (9+1,5x) \cdot 8 \cdot (10 – 0,96x) \\ &= \frac{1}{6} \cdot (9 + 1,5x) \cdot (80 – 7,68x) \\ &= \frac{1}{6} \cdot (720 – 69,12 x + 120x – 11,52x^2) \\ &= \frac{1}{6} \cdot (-11,52x^2 + 50,88x + 720) \\ \Rightarrow &V_{Pyramide} = (-1,92x^2 + 8,48x + 120) cm^3 \end{align}
Zurück zum MAP-Hack:

Lösung zu B2.5
\begin{align} &T_{max}\, mit \, dem \, GTR: \\ -1,92x^2 + 8,48 x + 120 & \Rightarrow V_{max} = 129,39 cm^3 \\ \\ &V_{gesamt} \, mit \, der \, Volumenformel: \\ V_{gesamt} &= \frac{1}{3} \cdot A_G \cdot h \\&= \frac{1}{3} \cdot \frac{1}{2} \cdot \overline{AC} \cdot \overline{BD} \cdot \overline{AS} \\ &= \frac{1}{3} \cdot \frac{1}{2} \cdot 9 \cdot 8 \cdot 10 \\ \Rightarrow &V_{gesamt} = 120 cm^3 \\ \\ &p \, mit \, der \, Prozentformel: \\ p &= \frac{V_{max}}{V_{gesamt}} \cdot 100 \% \\ &= \frac{129,38}{120} \cdot 100 \% \\ \Rightarrow &p = 107,82 \% \end{align}
Das größte Volumen ist um 7,82 % größer.
Zurück zum MAP-Hack:
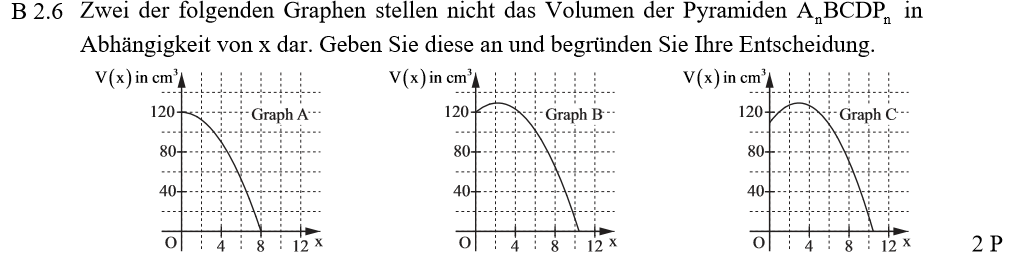
Lösung zu B2.6
Du kannst die Aufgabe durch Ausschluss lösen. Der Graph A ist das maximale Volumen bei 120, das darf aber nicht sein. Bei Graph C ist das Volumen für x = 0 nicht 120, sondern ungefähr 110. Auch das darf nicht sein. Es bleibt nur der Graph von B übrig.

Hallo ,
wieso ist bei der 2.5 AS die Höhe und nicht MS?
Tue mich immer schwer zu wissen was die Höhe ist…
Hey,
da eine Höhe immer Senkrecht auf der Grundfläche stehen muss (also mit 90°) kommt die Strecke AS als einzige Höhe von Pyramide ABCDS infrage. Die Höhe die du meinst (MS) würde in der Grundfläche liegen und bei einer Volumina Berechnung z.b auch in der Grundflächenberechnung mit drinnen sein.
Ich hoffe ich konnte dir damit helfen
Du hast eine Frage zu einer Teilaufgabe oder zur Lösung? Schreib‘ hier und du bekommst eine Antwort!