

Lösung zu B2.1
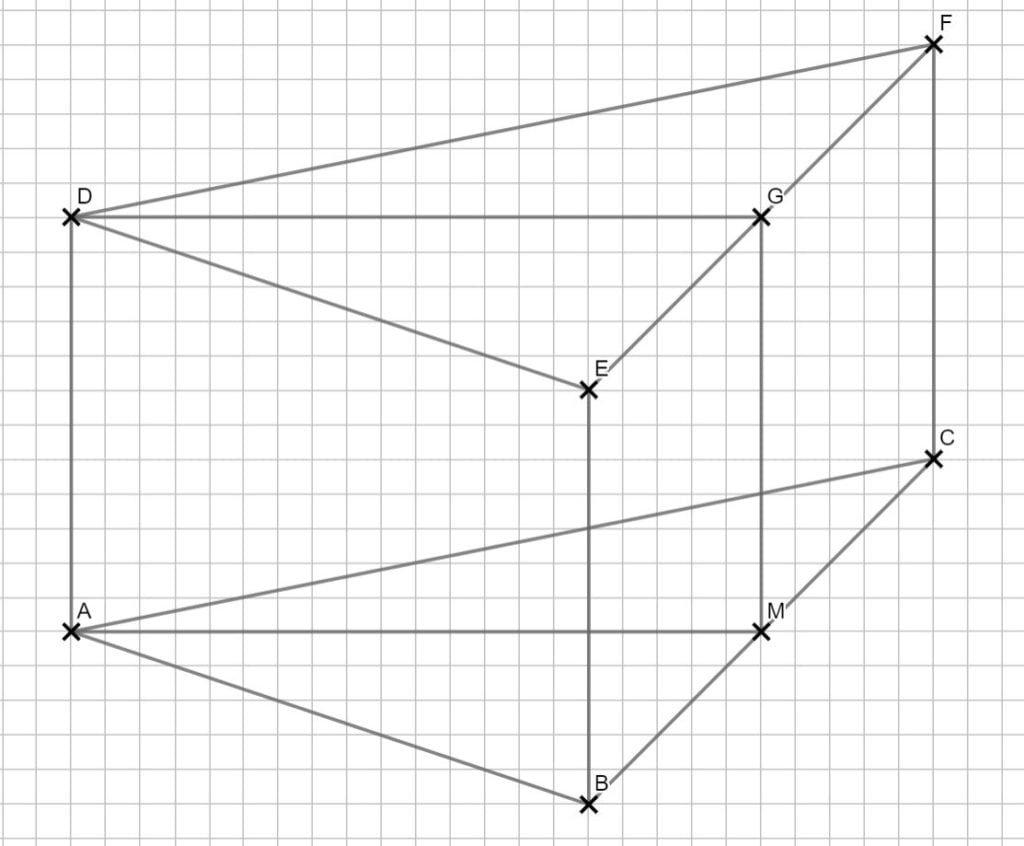
\begin{align} &\overline{AG} \text{ mit dem Satz des Pythagoras:}\\
\overline{AG}^2&= \overline{AM}^2 + \overline{AD}^2\\
&= 10^2 + 6^2 \\
\Rightarrow &\overline{AG} &= 11,66 \text{cm} \\
\\
&\varphi \text{ mit dem Tangens:}\\
tan(\varphi) &= \frac{\, \overline{AM} \,}{\overline{AG}}\\
&= \frac{10}{6} \\
\Rightarrow &\varphi = 59,04 °\end{align}
Zurück zum MAP-Hack:

Lösung zu B2.2

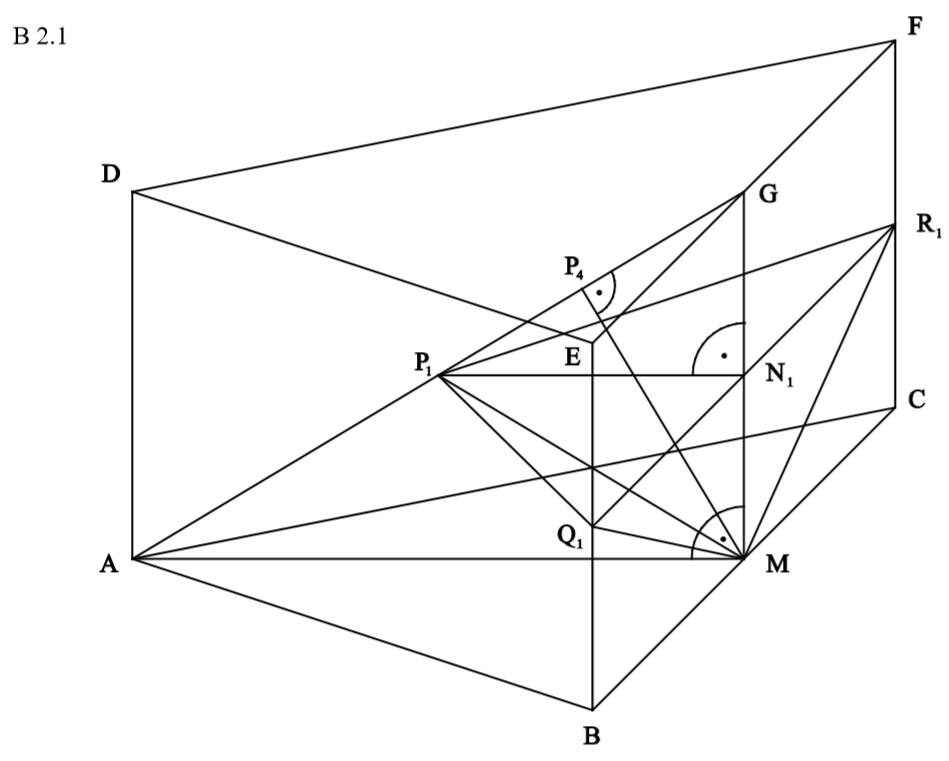
Zurück zum MAP-Hack:

Lösung zu B2.3
Es handelt sich um eine Pyramide mit dreieckiger Grundfläche, also kannst du mit der Formel \( V = \frac{1}{3} \cdot A_g \cdot h \) rechnen. Hierfür brauchst du die Länge der Strecke \( \overline{P_n N_n}\). Diese kannst du mit dem Vierstreckensatz bestimmen:
\begin{align} &\overline{P_n N_n} \text{ mit dem Vierstreckensatz:}\\
\frac{\, \overline{P_n N_n}}{\overline{AM}} &= \frac{x}{\, \overline{AD} \,} \,\,\, |\cdot \overline{AM}\\
\overline{P_n N_n} &= \frac{x}{\, \overline{AD}\,} \cdot \overline{AM} \\
&=\frac{x}{6} \cdot 10 \\
\Rightarrow &\overline{P_n N_n} = 1,67x \\
\\
&V \text{ mit der Volumenformel:}\\
V &= \frac{1}{3} \cdot A_g \cdot h \\
\\
&\text{ mit } A_g = 0,5 \cdot \overline{P_n N_n} \cdot \overline{BC} \\
&text{und } h = \overline{N_n M} = 6-x\\
\\
V &= \frac{1}{3} \cdot (\frac{1}{2} \cdot 1,67x \cdot 14) \cdot (6 -x ) \\
\Rightarrow &V(x) = (-3,90x^2 + 23,38x ) \text{ FE} \end{align}
Zurück zum MAP-Hack:

Lösung zu B2.4
\begin{align} &V_{P_0 Q_0 R_0 M} \text{ mit dem GTR:} \\
\text{Berechne den Extremwert von } &V(x) = -3,90x^2 + 23,38x \text{ mit dem GTR:} \\
\Rightarrow &V_{max} = V_{P_0 Q_0 R_0 M} = 35,04 \\
\\
& V_{ABCDEF} \text{ mit der Volumenformel:}\\
V_{ABCDEF}&= \frac{1}{2} \cdot \overline{BC} \cdot \overline{AM} \cdot \overline{AD} \\
&= \frac{1}{2} \cdot 14 \cdot 10 \cdot 6 \\
\Rightarrow &V_{ABCDEF} = 420 \\
\\
&p \text{ mit der Prozentformel:}\\
p &= \frac{ \text{Anteil}}{\text{Ganzes}} \cdot 100 \% \\
&= \frac{420 – 35,03}{420} \cdot 100 \% \\
\Rightarrow p = 91,66 \% \end{align}
Das Volumen ist um 91,66 % kleiner.
Zurück zum MAP-Hack:
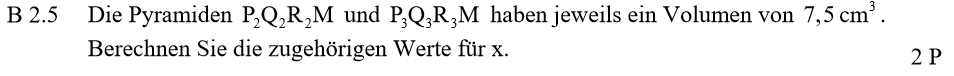
Lösung zu B2.5
Um die Aufgabe zu lösen, setzt die du Volumenformel aus 2.3 mit 7,5 gleich, löst nach „=0“ auf und lässt den GTR die quadratische Gleichung lösen:
\begin{align} V(x) &= 7,5 \\
-3,9x^2 + 23,38x &= 7,5 \,\,\, |-7,5 \\
-3,9x^2 + 23,38x -7,5&= 0 \\
\Rightarrow >R \Rightarrow x = 0,34 \, \lor \, x = 5,65 \end{align}

Lösung zu B2.6
Das Dreieck PNM ist immer rechtwinklig, also kann du die Streckenlänge mit dem Satz des Pytagoras ausrechnen:
\begin{align} &\overline{P_n M} \text{ mit dem Satz des Pytagoras:}\\
\overline{P_ n M}^2 &= \overline{P_n N_n}^2 + \overline{N_n M}^2 \\
&= (1,67x)^2 + (6 – x)^2 \\
&= 2,79x^2 + (36 – 12x + x^2) \\
&= 3,79x^2 -12x + 36 \,\, \, |\sqrt{}\\
\Rightarrow &\overline{P_n M} = \sqrt{3,79x^2 -12x + 36} \\
\\
& \text{Extremwertbestimmung mit dem GTR:}\\
\Rightarrow &\text{Minimum:} \overline{P_4 M} = 5,15 \text{cm} \end{align}

Da steht gar nix die Schultablets sind scheiße
Das klingt nach einem Internet-Connection-PRroblem, als ob die Inhalte nicht laden.
Probier es doch mal in einem anderen Netzwerk oder mit einem anderen Browser.