

Lösung zu B2.1
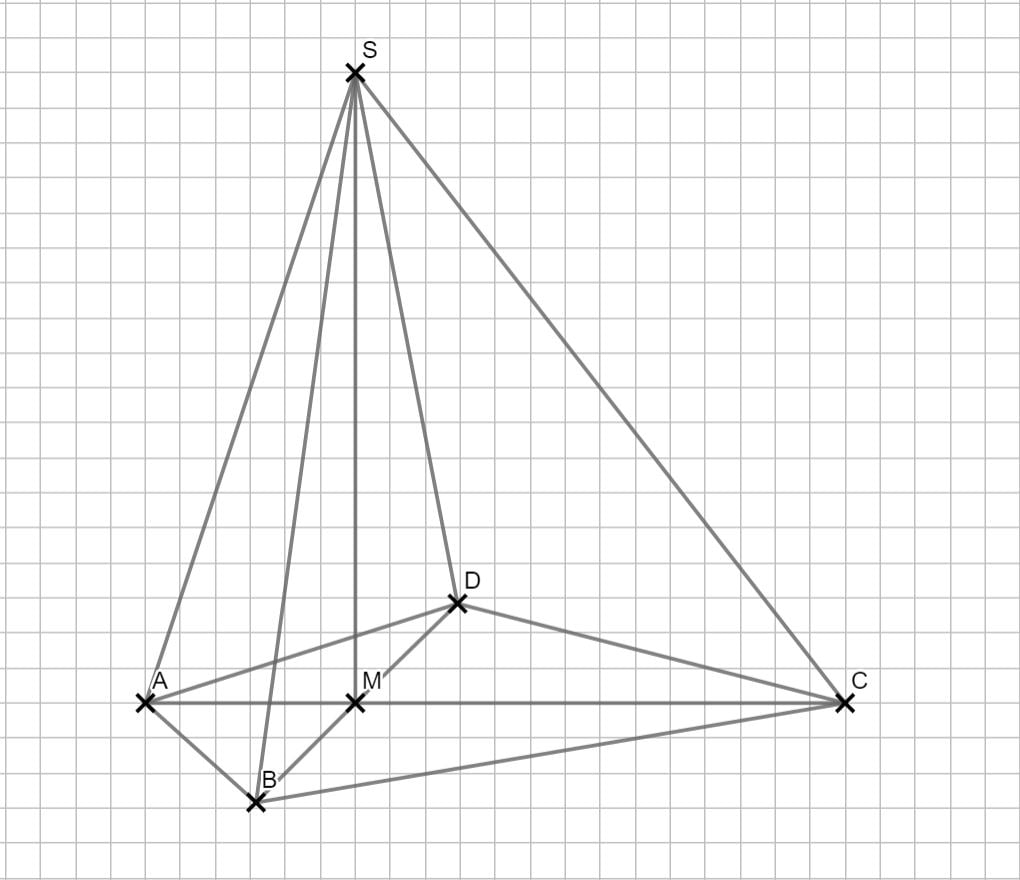
\begin{align} &\overline{SC} \text{ mit dem Satz des Pythagoras:}\\
\overline{SC}^2 &= \overline{MC}^2 + \overline{MS} \\
&= 7^2 + 9^2 \,\,\ |\sqrt{} \\
\Rightarrow &\overline{SC} = 11,40 \text{ cm}\\
\\
&\angle SCA \text{ mit dem Tangens:}\\
tan(\angle SCA) &= \frac{\, \overline{MS} \,}{\overline{MC}}\\
&= \frac{9}{7} \\
\Rightarrow &\angle SCA = 52,13° \end{align}
Zurück zum MAP-Hack:

Lösung zu B2.2
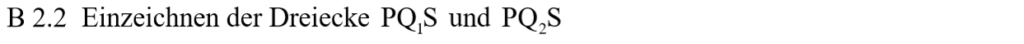
Zurück zum MAP-Hack:
Lösung zu B2.3
Um die gesuchte Streckenlänge zu bestimmen, benötigst du den Winkel ASC. Diesen kannst du aus der Innenwinkelsumme berechnen, wenn du erst den Winkel MAS bestimmst.
\begin{align} &\angle MAS \text{ mit dem Tangens:}\\
tan(\angle MAS) &= \frac{\, \overline{MS} \,}{\overline{AM}}\\
&= \frac{9}{3} \\
\Rightarrow &\angle MAS = 71,57° \\
\\
&\angle ASC \text{ über die Innenwinkelsumme:}\\
\angle ASC &= 180° – \angle MAS – \angle SCA \\
&= 180° – 71,57° – 52,13° \\
\Rightarrow &\angle ASC = 56,30° \\
\\
&\overline{SQ_1} \text{ mit dem Cosinus:}\\
cos(\angle ASC) &= \frac{\, \overline{SQ_1} \,}{\overline{PS}}\\
cos(56,30°) &= \frac{\, \overline{SQ_1} \,}{4} \,\,\, |\cdot 4 \\
\overline{SQ_1}&= cos(56,30°) \cdot 4 \\
\Rightarrow &\overline{SQ_1} = 2,22 cm\end{align}
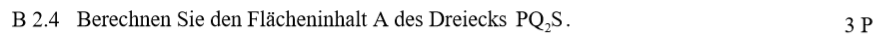
Lösung zu B2.4
Zuerst du musst dir klar werden, was du alles brauchst. Schreibe dir die Formel einmal auf:
\begin{align} \text{Ziel:} A &= 0,5 \cdot \overline{SP} \cdot \overline{PQ_2} \cdot sin(\angle Q_2 PS) \\
\\
\angle Q_2 PS &= \angle MAS = 71,57° \\
\\
&\overline{PQ_2} \text{ mit dem Sinussatz:}\\
\angle SQ_2 P &= \angle SCA = 52,13° \\
\frac{\, \overline{PQ_2} \,}{sin(\angle PSQ_2)} &= \frac{\, \overline{PS} \,}{sin(\angle SQ_2 P)} \\
\frac{PQ_2}{sin(56,30°)} &= \frac{4}{sin(52,13°)} \,\,\,|\cdot sin(56,30°) \\
\overline{PQ_2} &= \frac{4}{sin(52,13°)} \cdot sin(56,30°) \\
\Rightarrow &\overline{PQ_2} = 4,22 \text{ cm}\\
\\
&\text{Einsetzen in die Flächenformel:}\\
A &= 0,5 \cdot \overline{SP} \cdot \overline{PQ_2} \cdot sin(\angle Q_2 PS)\\
&= 0,5 \cdot 4 \cdot 4,22 \cdot sin(71,57°) \\
\Rightarrow &A= 8,01 \text{cm}^2 \end{align}
Zurück zum MAP-Hack:

Lösung zu B2.5
Das Ziel ist, über den Sinus der gesuchten Streckenlänge \( \overline{F_3 Q_3} \) zu berechnen. Dafür brauchst du die Streckenlänge \( \overline{SQ_3}\), die du über den Sinus-Satz bestimmen kannst… und dafür brauchst du weiderrum den Winkel \( SQ_3 P\). Na gut, dann gehen wir es mal an:
\begin{align} \text{Ziel: } sin(\angle SCA) &= \frac{\overline{F_3 Q_3}}{\overline{SC} – \overline{SQ_3}} \\
\\
&\angle SQ_3 P \text{ über die Innenwinkelsumme:}\\
\angle SQ_3 P &= 180° – \angle Q_3 PS – \angle PSQ_3 \\
&= 180° – 77° – 56,30° \\
\Rightarrow &\angle SQ_3 P = 46,70° \\
\\
&\overline{SQ_3} \text{ mit dem Sinussatz:}\\
\frac{\overline{SQ_3}}{sin(\angle Q_3 PS)} &= \frac{\overline{PS}}{sin(\angle SQ_3P)}\\
\frac{\overline{Q_3}}{sin(77°)}&= \frac{4}{sin(46,70°)} \,\,\, |\cdot sin(77°)\\
\overline{SQ_3} &= \frac{4}{sin(46,70°)} \cdot sin(77°) \\
\Rightarrow &\overline{SQ_3} = 5,36 \text{cm} \\
\\
&\overline{F_3 Q_3} \text{ mit dem Sinus:}\\
sin(\angle SCA) &= \frac{\overline{F_3 Q_3}}{\overline{SC} – \overline{SQ_3}} \\
sin(52,13°) &= \frac{\overline{F_3 Q_3}}{11,40 – 5,36} \,\,\, |\cdot (11,40 – 5,36)\\
\overline{F_3 Q_3} &= sin(52,13°) \cdot (11,40 – 5,36) \\
\Rightarrow &\overline{F_3 Q_3} = 4,77 \text{cm}\end{align}
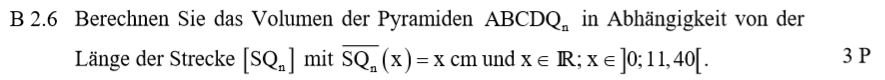
Lösung zu B2.6
\begin{align} \text{Ziel: }V(x) &= \frac{1}{3} \cdot A_g \cdot h\\
&\text{mit } A_g = 0,5 \cdot \overline{AC} \cdot \overline{BD} \\
&\text{und }h = \overline{F_n Q_n} \\
\\
&\overline{F_n Q_n} \text{ mit dem Sinus:}\\
sin(\angle SCA) &= \frac{\, \overline{F_n Q_n}\,}{\overline{C Q_n}} \\
sin(52,13°) &= \frac{\overline{F_n Q_n}}{11,40 – x} \,\,\, \cdot(11,40 -x)\\
\Rightarrow &\overline{F_n Q_n} = 9,00 – 0,79x \\
\\
&\text{Einsetzen in die Volumenformel:}\\
V &= \frac{1}{3} \cdot 0,5 \cdot \overline{AC} \cdot \overline{BD} \cdot \overline{F_n Q_n}\\
&= \frac{1}{3} \cdot 0,5 \cdot 10 \cdot 8 \cdot (9,00 – 0,79x)\\
\Rightarrow &V = (120 – 10,53x) \text{cm}^3 \end{align}
