2015 Haupttermin B2: Raumgeometrie

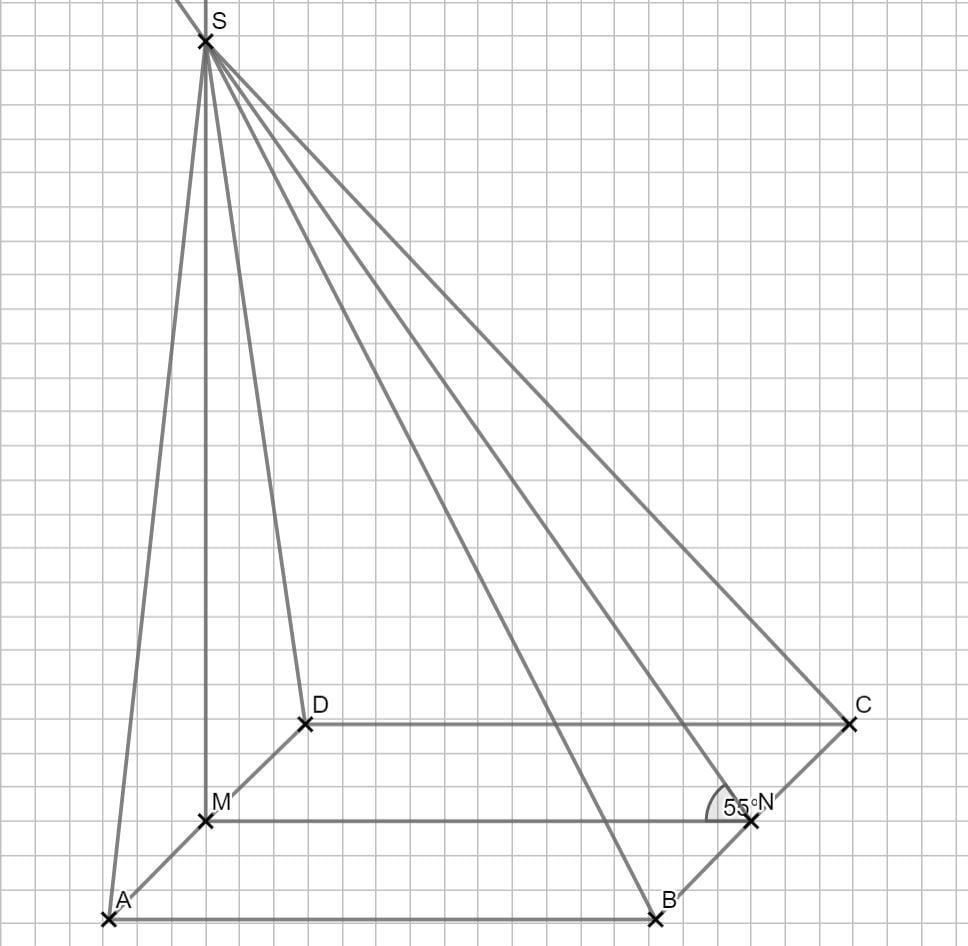
\begin{align} \overline{MS} \text{ mit dem Tangens:}\\
tan(\angle SNM) &= \frac{\, \overline{MS} \,}{\overline{MN}} \,\,\, |\cdot \overline{MN}\\
\overline{MS} &= \overline{MN} \cdot tan(\angle SNM) \\
&=8 \cdot tan(55°)\\
\Rightarrow &\overline{MS} = 11,43 \text{cm}\\
\\
\overline{SN} &\text{mit dem Cosinus:}\\
\cos(\angle SNM) &= \frac{\, \overline{MN} \,}{\overline{SN}} \,\, | \cdot \overline{SN} \, :cos(\angle SNM)\\
\overline{SN} &= \frac{\overline{MN}}{cos(\angle SNM)} \\
&= \frac{8}{cos(55°)}\\
\Rightarrow &\overline{SN} = 13,95 \text{cm}\end{align}

Einzeichnen der Pyramide

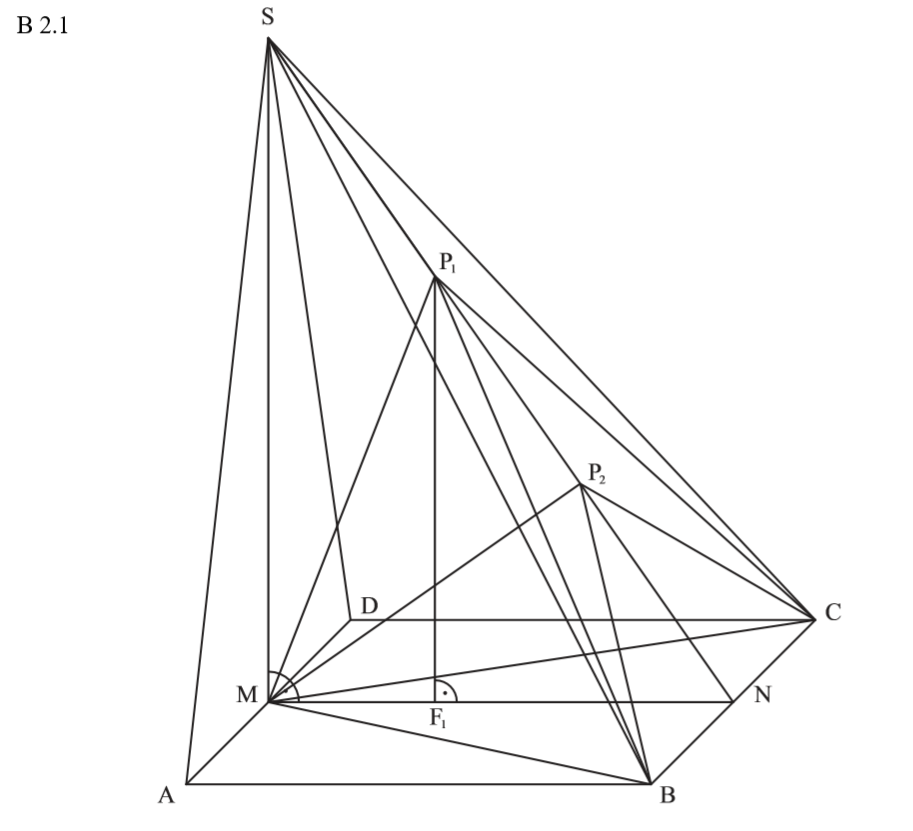
\begin{align} &\angle MSN \text{ über die Innenwinkelsumme:}\\
\angle MSN &= 180° – \angle NMS – \angle SNM \\
&=180° – 90° – 55° \\
\Rightarrow &\angle MSN = 35° \\
\\
& \overline{MP_1} \text{ mit dem Cosinussatz:}\\
\overline{MP_1} &= \overline{MS}^2 + \overline{P_1 S}^2 – 2 \cdot \overline{MS} \cdot \overline{P_1 S} \cdot cos(\angle MSN) \\
&= 11,43^2 + 5^2 – 2 \cdot 11,43 \cdot 5 \cdot cos(35°) \\
\Rightarrow &\overline{MP_1} = 7,88 \text{cm}\\
\\
&\angle SP_1 M \text{ mit dem umgeformten Cosinussatz:}\\
cos(\angle SP_1 M) &= \frac{ \, \overline{MP_1}^2 + \overline{P_1 S}^2 – \overline{MS}^2 \,}{2 \cdot \overline{MP_1} \cdot \overline{P_1 S}} \\
&=\frac{\, 7,88^2 + 5^2 -11,43^2 \, }{2 \cdot 7,88 \cdot 5} \\
\Rightarrow &\angle SP_1 M = 123,55° \end{align}

Um das Volumen zu bestimmen, benötigst du die Höhe \( h = \overline{F_n P_n} \) . Hierfür berechnest du die zuerst die Länge \( \overline{NP_n} \).

\begin{align} \overline{NP_n} &=\overline{SN} – x \\
&= 13,95 -x\\
\\
&\overline{P_n F_n} \text{ über den Sinus:}\\
sin(\angle P_n N F_n) &= \frac{\, \overline{P_n F_n} \,}{\overline{NP_n}} \,\,\, |\cdot \overline{NP_n}\\
\overline{P_n F_n} &= \overline{NP_n } \cdot sin(\angle P_n N F_n) \\
&= (13,95 – x) \cdot sin(55°) \\
\Rightarrow &\overline{P_n F_n}(x) = (-0,82x + 11,43) \text{ cm}\\
\\
&V \text{ über die Volumenformel:}\\
V &= \frac{1}{3} \cdot (\frac{1}{2} \cdot \overline{AB}^2 ) \cdot \overline{P_n F_n}\\
&= \frac{1}{3} \cdot \frac{1}{2} \cdot 8^2 \cdot(-0,82x + 11,42) \\
\Rightarrow &V(x) = (-8,75x + 121,92) \text{cm}^3 \end{align}

\begin{align} V &= \frac{1}{3} \cdot \overline{AB}^2 \cdot \overline{MS} \\
&= \frac{1}{3} \cdot 8^2 \cdot 11,43 \\
\Rightarrow &V = 243,83 \text{ cm}^3
\\
V(x) &= 0,34 \cdot V \\
-8,75x + 121,92 &> 0,34 \cdot 243,83 \\
-8,75x + 121,92 &> 82,91 \,\,\, |- 121,92 \\
-8,75x &> -39,01 \,\,\, |:(-8,75) \, \text{ Inversionsgesetz!}\\
x &< 4,46 \end{align}

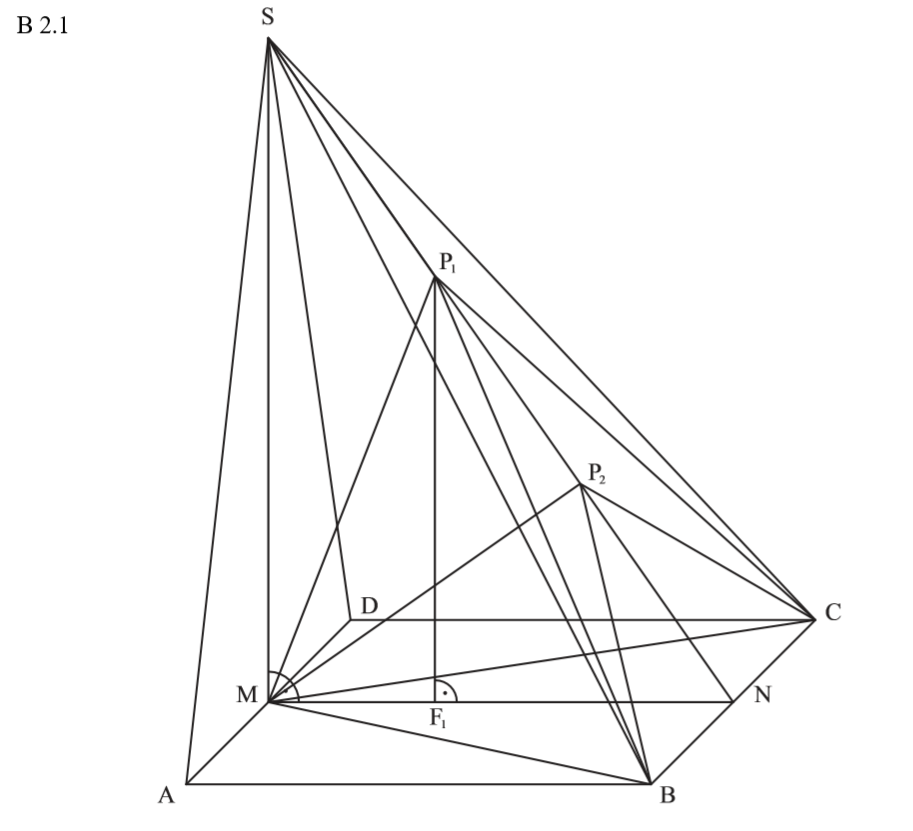
Weil im Punkt \( P_2 \) die kürzeste Entfernung zu M gilt, ist dort auch ein rechter Winkel. Zeichne die Pyramide ein und arbeite mit dem rechten Winkel.

\begin{align} &\overline{MP_2} \text{ mit dem Sinus:}\\
sin(\angle P_2 NM) &= \frac{\, \overline{MP_2} \,}{\overline{MN}}\,\,\, |\cdot \overline{MN}\\
\overline{MP_2} &= \overline{MN}\cdot sin(\angle P_2 NM) \\
&= 8 \cdot sin(55°) \\
\Rightarrow &\overline{MP_2} = 6,55 \text{cm} \\
\\
&x \text{ mit dem Tangens:}\\
tan(\angle MSP_2 ) &= \frac{\, \overline{MP_2} \,}{x} \,\,\, |\cdot x : tan(\angle MSP_2 ) \\
x &= \frac{\overline{MP_2}}{tan(\angle MSP_2 )} \\
&= \frac{6,55}{tan(35°)}\\
\Rightarrow &x = 9,35 \text{ cm} \end{align}