

Lösungen zu 2.1
Schau dir die Skizze an und zeichne dieses Bild in den angegebenen Maßen.
Zurück zum MAP-Hack:

Lösungen zu 2.2
Die Höhe steht immer senkrecht. Du kannst also mit Sin/Cos/Tan und dem Satz des Pythagoras arbeiten.
\begin{align} &|\overline{AS}| \text{ mit dem Satz des Pythagoras:}\\
|\overline{AS}|^2 &= |\overline{AM}|^2 + |\overline{MS}|^2 \\
&= 9^2 + 10^2 \,\,\, |\sqrt{}\\
&\Rightarrow |\overline{AS}| = 13,45 cm\\
\\
&\angle MAS \text{ mit dem Tangens:}\\
tan(\angle MAS) &= \frac{|\overline{MS}|}{|\overline{AM}|} \\
&= \frac{10}{9}\,\,\, |tan^{-1}\\
&\Rightarrow \angle MAS = 48,01° \\
\\
&\text{Berechnung des Volumens:}\\
V_{ABCS} &= \frac{1}{3} \cdot \frac{1}{2} \cdot |\overline{AM}| \cdot |\overline{BC}| \cdot |\overline{MS}| \\
&= \frac{1}{3} \cdot \frac{1}{2} \cdot 9 \cdot 12 \cdot 10 \\
&\Rightarrow V_{ABCS} = 180 cm^3 \end{align}
Zurück zum MAP-Hack:

Lösungen zu 2.3
Für den Winkel DMA fehlt dir eine Angabe. Warum muss man wohl DM einzeichnen?
Achtung, du hast keine rechten Winkel mehr! Aber es gibt ja noch andere Ansätze.
\begin{align} &|\overline{DM}| \text{ mit dem Cosinussatz:}\\
|\overline{DM}|^2 &= |\overline{AD}|^2 + |\overline{AM}|^2 – 2 \cdot |\overline{AD}| \cdot |\overline{MA}| \cdot cos(\angle MAS) \\
&= 4^2 + 9^2 – 2 \cdot 4 \cdot 9 \cdot cos(48,01°) \,\,\, |\sqrt{}\\
&\Rightarrow |\overline{DM}| = 6,99 cm\\
\\
&\angle DMA \text{ mit dem Sinussatz:}\\
\frac{sin(\angle DMA)}{|\overline{AD}|} &= \frac{sin(\angle MAS)}{|\overline{DM}|} \,\,\, |\cdot |\overline{AD}| \\
sin(\angle DMA) &= \frac{sin(\angle MAS)}{|\overline{DM}|} \cdot |\overline{AD}| \\
&= \frac{sin(48,01°)}{6,99} \cdot 4 \,\,\, |sin^{-1}\\
&\Rightarrow \angle DMA = 25,17° \end{align}
Zurück zum MAP-Hack:
Das Vorgehen für diese Aufgabe liest du dir am besten im Ebene Geometrie – Hack durch, der hier verlinkt ist.

Lösungen zu 2.4
Schaue immer zuerst nach dem Wert für x. Hier also 5.
Siehe B2.1
Zurück zum MAP-Hack:

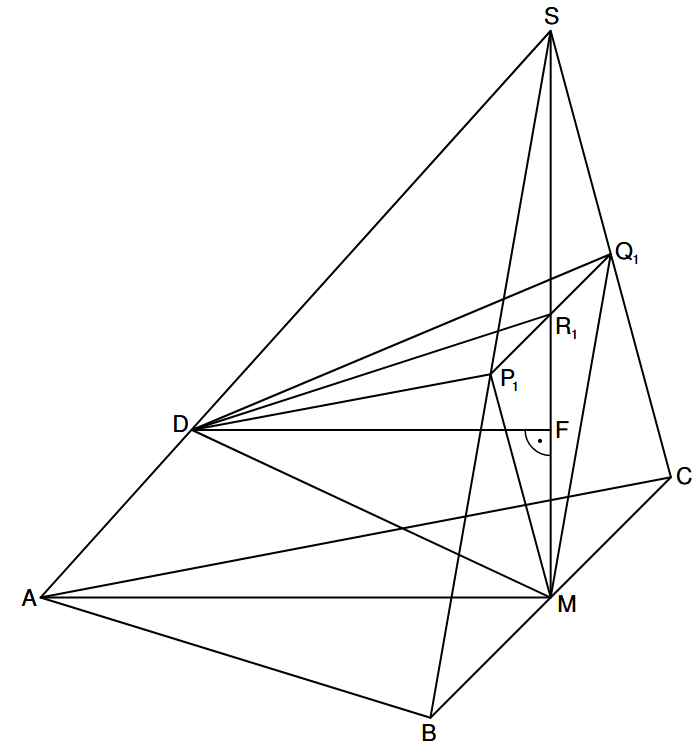
Lösungen zu 2.5
PQ bekommst du mit dem Vierstreckensatz.
\begin{align} &\text{Ansatz zur Lösung:}\\
V &= \frac{1}{3} \cdot A_G \cdot h \\
&\text{mit }A_G = A_{PMQ} = \frac{1}{2} \cdot |\overline{P_n Q_n}| \cdot |\overline{RM}|\\
\\
&|\overline{P_n Q_n}| \text{ mit dem Vierstreckensatz:}\\
\frac{|\overline{P_n Q_n}|}{|\overline{BC}|} &= \frac{|\overline{SR_n}|}{|\overline{MS}|} \,\,\, |\cdot |\overline{BC}|\\
|\overline{P_n Q_n}| &= \frac{|\overline{SR_n}|}{|\overline{MS}|} \cdot |\overline{BC}| \\
&= \frac{x}{10} \cdot 12 \\
&\Rightarrow |\overline{P_n Q_n}| = 1,2x \\
\\
&\text{Einsetzen in } A_{PMQ}:\\
|\overline{RM}| &= 10 – x \\
A_{PMQ} &= \frac{1}{2} \cdot |\overline{P_n Q_n}| \cdot |\overline{RM}|\\
&= \frac{1}{2} \cdot 1,2x \cdot (10 – x) \\
&\Rightarrow A_{PMQ} = 6x – 0,6x^2 \\
\\
&|\overline{DF}| \text{ mit dem Vierstreckensatz:}\\
\frac{|\overline{DF}|}{|\overline{AM}|} &= \frac{|\overline{DS}|}{|\overline{AS}|} \,\,\, |\cdot |\overline{AM}| \\
|\overline{DF}| &= \frac{9,45}{13,45} \cdot 9 \\
&\Rightarrow |\overline{DF}| = 6,32 cm \\
\\
&\text{Einsetzen in den Ansatz:}\\
V &= \frac{1}{3} \cdot A_{PMQ}\cdot h\\
&=\frac{1}{3} \cdot (6x – 0,6x^2) \cdot 6,32 \,\,\, \text{ 6,32 und 1/3 in die Klammer multiplizieren} \\
&\Rightarrow V = (-1,26x^2 + 12,64x) cm^3 \end{align}
Zurück zum MAP-Hack:

Lösungen zu 2.6
Wenn etwas um 90% kleiner ist, dann bleiben 10% übrig. Setze damit eine Gleichung an.
\begin{align} V(x) &= 10 \% \cdot V \\
-1,26x^2 + 12,64x &= 0,1 \cdot 180 \,\,\, |-18 \\
-1,26x^2 + 12,64 x – 18 &= 0 \\
\Rightarrow GTR: \, x_1 = 8,31 \,\, & \, \, x_2 = 1,72 \end{align}

wieso konnte man beim VSS für DF nicht die Strecke MS und SR1 verwenden also 10 cm und 5 cm, sondern musste AS und DS nehmen?
Hallo! Schön, dass du fragst!
Für den VSS brauchst du ja immer ein paar parallele Seiten. Wenn du MS und SR1 nimmst, dann hast du keine parallele Seite durch R1.Außerdem hat ja SR1 keine Gemeinsamkeit mit DF.
Ich bin mir gerade nicht sicher, ob ich deine Frage richtig verstanden habe. Frage also gerne nochmal, wenn das noch nicht geholfen hat.
Hallo, ich hätte eine Frage, die eher allgemein formuliert ist. Sie sind ja Lehrer an einer Realschule, richtig? Dann kennen Sie sich doch sicherlich auch mit den Noten einer Abschlussprüfung aus(: Und zwar wollte ich wissen, ob man mit einer 6 in Wirtschaft durchfällt … Betrifft zwar kein Mathe, aber vielleicht wissen Sie davon Bescheid. Soweit ich weiß war es ja immer so, dass man in Deutsch mit einer 6 durchfällt. Doch gilt das auch für die anderen Fächer?
Die Regel mit Note 6 durchgefallen gibt es NUR IN DEUTSCH. Mit einer 6 in einer anderen Prüfung ist man noch nicht durchgefallen.