Rechnen im rechtwinkligen Dreieck
Das Rechnen im rechtwinkligen Dreieck ist eine Vorarbeit zum Rechnen im allgemeinen Dreieck. Wir wiederholen schnell die Rechenmethoden aus der 9. Klasse und dann darfst du direkt an Abschlussprüfungsaufgaben üben.
Der Satz des Pythagoras
Dieser Satz ist der erste, der dir in den Sinn kommen muss, wenn du rechtwinkliges Dreieck liest. Wenn du gerne mal was vergisst, schreibe einfach „Py“ über das Wort rechtwinklig, dann findest du später bestimmt einen Ansatz.
Ist ein Dreieck rechtwinklig, dann ist das Hypotenusen-Quadrat gleich der Summe der Katheten-Quadrate.
\( \text{Hyp}^2 = \text{Kath}^2 + \text{Kath}^2 \)
Die Formel in dieser Form wird deinen Lehrer stören, schreibe sie also nicht auf eine Schulaufgabe oder Prüfung! Um sich den Satz zu merken, finde ich sie aber super.
In der Standardbeschriftung eines Dreiecks sind a und b die Katheten und c die Hypotenuse und so ergibt sie die „Formel“ \( a^2 + b^2 = c^2 \). Der Satz des Pythagoras ist in dieser Form leider nicht hilfreich, also merke es dir lieber mit den Katheten. Formt man den Satz des Pytagoras nach einer Kathete um, so erhält man:
\( \text{Kath}^2 = \text{Hyp}^2 – \text{Kath}^2 \)
Sinus, Cosinus, Tangens
Du weiß bestimmt, hier kommen die Ankathete, die Gegenkathete und die Hypotenuse ins Spiel, aber wie war das jetzt genau? Je blödsinniger der Merkspruch, desto hilfreicher. Hier kommt die GAGA HühnerHof AG. Hier kommt noch der Cotan darin vor, den vergessen wir mal großzügig.
| Sin | Cos | Tan | Cotan |
| G | A | G | A |
| H | H | A | G |
Nicht begeistert von der GAGA HH AG? Dein Mathelehrer macht auch mal einen schlechten GAG? Die Schüler lachen nicht wirklich und bringen nur ein verschlucktes Lachen HHA raus.
| Sin | Cos | Tan |
| G | A | G |
| H | H | A |
Und jetzt nochmal in der Bruchschreibweise:
\( sin(\, \text{Winkel} \,) = \frac{\text{Gegenkathete}\,}{\, \text{Hypotenuse}\,} \)
\( sin(\, \text{Winkel} \,) = \frac{\text{Ankathete}\,}{\, \text{Hypotenuse}\,}\)
\( tan(\, \text{Winkel} \,) = \frac{\text{Gegenkathete}\,}{\, \text{Ankathete}\,} \)
Der Ansatzfinder
Und hier ist er – der Ansatzfinder! Ein Flowchart, der dir immer den passenden Ansatz ausspuckt.
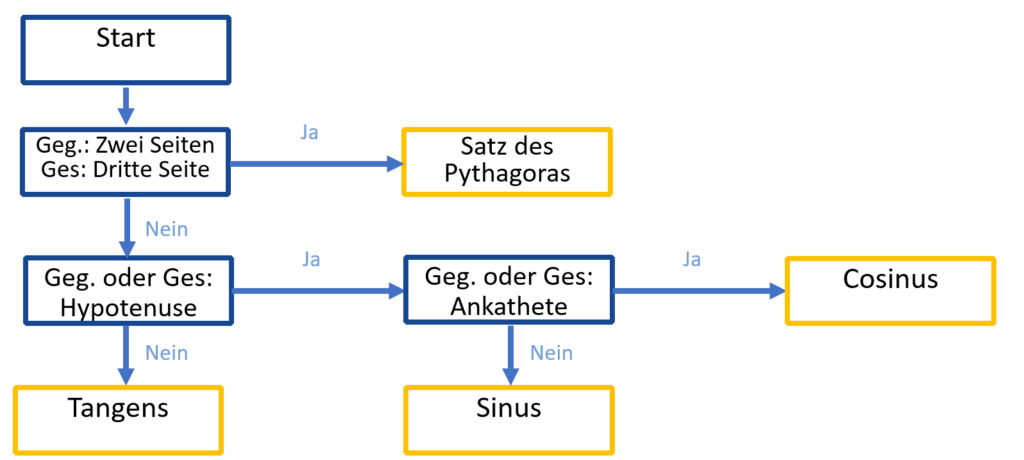
Einfach auswendiglernen oder ausdrucken und neben die Aufgaben legen, bis du es von alleine kannst.
MAPs zum Üben
>> Hier << gibt es auch ein Kahoot zum Finden des richtigen Ansatzes. Dein Lehrer startet es bestimmt gerne im Unterricht. Viel Spaß damit!
