

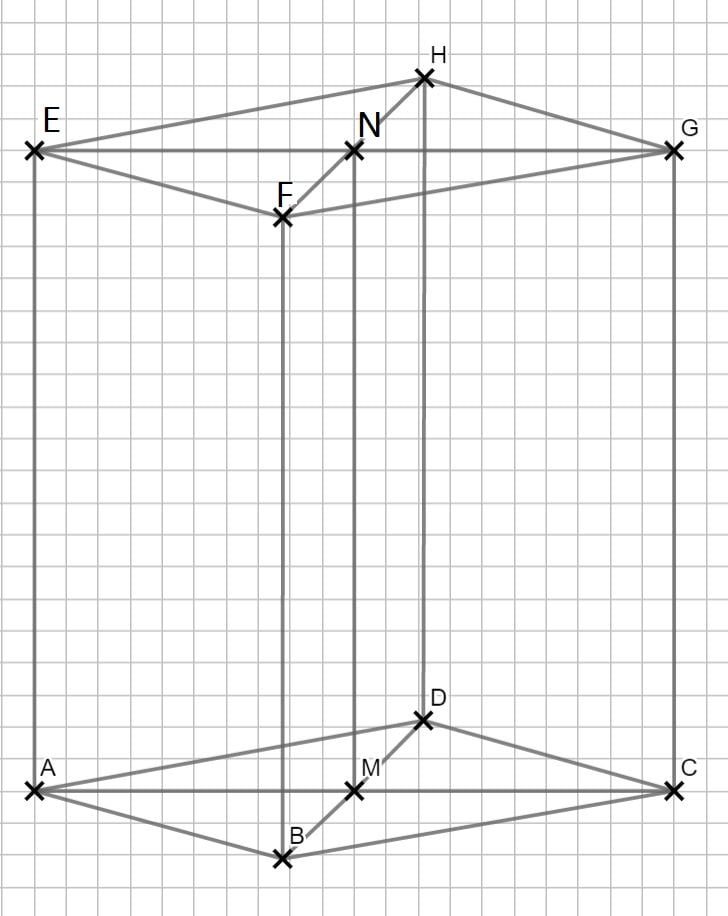
Lösung zu B2.1
Zurück zum MAP-Hack:
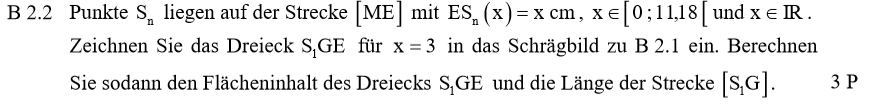
Lösungen zu B2.2
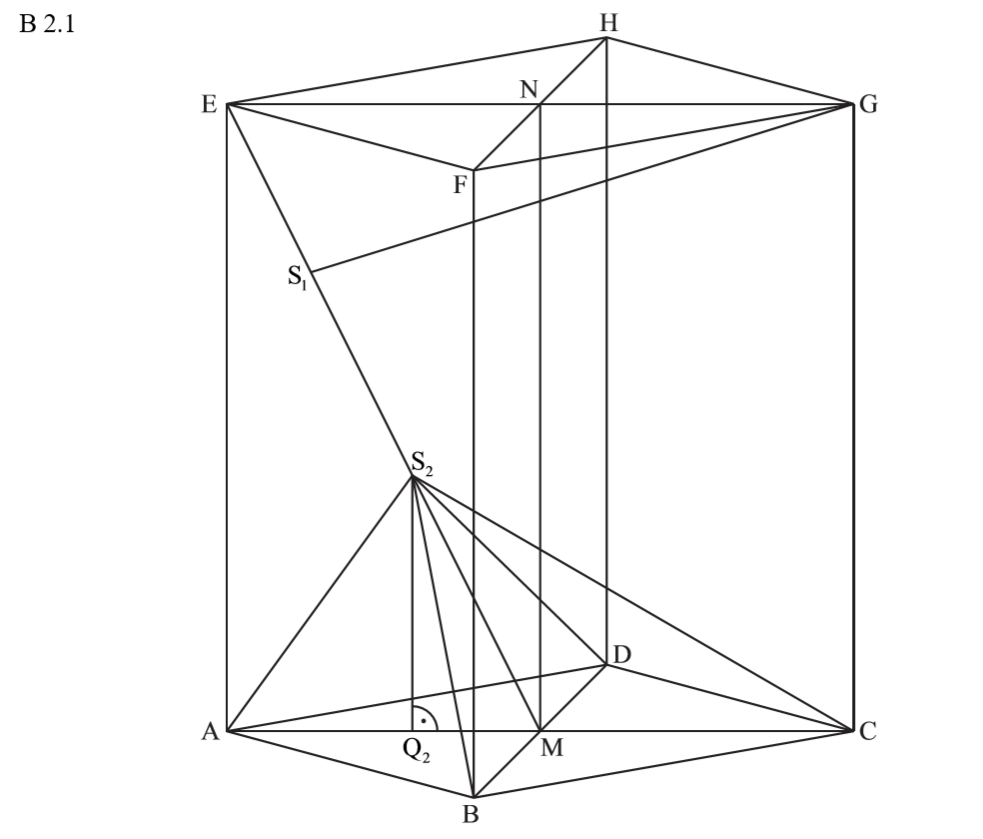
Zurück zum MAP-Hack:

Lösung zu B2.3
Zuerst bestimmst du die Höhe in Abhängigkeit von x, um diese dann in die Volumenformel der Pyramide einzusetzen:
\(\begin{align} \frac{\overline{Q_n S_n}}{\overline{AE}} &= \frac{\overline{MS_n}}{\overline{ME}} \, \, | \cdot \overline{AE} \\ \overline{Q_n S_n} &= \frac{\overline{M S_n}\cdot \overline{AE}}{\overline{AE}} \\ &= \frac{(11,18 – x) \cdot 10}{11,18} \\ &= 10 – \frac{10}{11,18} \cdot x \\ &= (10 – 0,89x) cm \end{align} \)Die Streckenlänge kann auch mit dem Sinus im \( Dreieck A_n MS_n \) berechnet werden.
\begin{align} & Berechnung \, des \, Volumens \, V_{ABCDS_n}: \\ V &= \frac{1}{3} \cdot \frac{1}{2} \cdot \overline{AC} \cdot \overline{BD} \cdot \overline{Q_n S_n} \\ &= \frac{1}{3} \cdot \frac{1}{2} \cdot 10 \cdot 6 \cdot (10- 0,89x) \\ \Rightarrow &V(x) = (100 – 8,9x) cm^3 \end{align}
Lösung zu B2.4
Zuerst berechnest du die passende Belegung für x, um dann auf das Volumen zu schließen. Hierzu verwendet man den Sinussatz. Die passenden Winkel musst du dir anhand der Innenwinkelsumme im Dreieck ausrechnen.
\begin{align} &x \, im \, Dreieck AMS_2: \\ \frac{\overline{MS_2}}{sin(\angle MAS_2)} &= \frac{\overline{AM}}{sin(\angle AS_2M)} \\ \frac{11,18 – x}{sin(54°)} &= \frac{5}{sin(180° – 63,43° – 54°)} \, \, \, |\cdot sin(54°) \\ 11,18 – x &= \frac{5 \cdot sin(54°)}{sin(62,57°)} \\ 11,18 – x &= 4,56 \, \, \, |+x – 4,56 \\ x &= 6,62 \\ \\ &V \, mit \, dem \, Ersatzergebnis: \\ V(x) &= 100 – 8,9 \cdot x \\ V(6,62) &= 100 – 8,9 \cdot 6,62 \\ \Rightarrow &V = 41,08 cm^3 \end{align}

Lösung zu B2.5
Unter allen Pyramiden ABCDS_n hat die Pyramide mit der Höhe \( \overline{AE} \) das größte Volumen. Diese entspricht auch der Höhe des Prismas. Die Grundflächen ABCD sind bei der Pyramide und dem Prisma gleich. Wir können direkt am größten Prisma-Volumen vergleichen:
\begin{align} V_{max Prisma} &= 0,5 \cdot \overline{AC} \cdot \overline{BD} \cdot \overline{AE} \\ &= 0,5 \cdot 10 \cdot 6 \cdot 10 \\ &= 300 cm^3 \\ \Rightarrow 0,5 \cdot V = 150 cm^3 \end{align}
Das Volumen der Pyramide (V = 100 – 8,9x) ist kleiner oder gleich 100. Also kann diesen Volumen nie 150 sein, denn 150 > 100.

Hallo ,
Kann ich bei der 2.4 nicht auch mithilfe des Vierstreckensatz Q2S2 raus rechnen ?
Bei mir kommt dann aber da 5,92 raus und somit liegt mein Ergebnis dann bei 59,2 cm3
Hallo Marko,
ich überblick gerade nicht ganz deinen Lösungsweg, aber 5,92 ist recht weit daneben. Du darfst hier gerne mal deinen Ansatz mit VSS schreiben, dann schaue ich mal drüber.
VIel Erfolg noch!
Tobias Cobanov
Du hast eine Frage zu einer Teilaufgabe oder zur Lösung? Schreib‘ hier und du bekommst eine Antwort!
Kann ich bei der 2.4 auch die Strecke Q2S2 berechnen und dann ganz normal in die Volumen Formel einsetzen? Ich habe das gemacht bei mir kam aber 40,8 cm³ raus…
Hallo Thorben,
wie hast du denn Q2S2 ausgerechnet? Da sehe ich gerade keinen möglichen Ansatz, aber vielleicht übersehe ich auch etwas.
Hallo, ich habe auch Q2S2 ausgerechnet, indem ich zuerst mit dem Sinussatz AS2 ausgerechnet habe und anschließend wieder mit dem Sinuss. Q2S2 ausgerechnet habe. Ich komme auch auf ein Volumen von 40,8cm3😅
Ah, der Sinussatz. Den mag ich ja persönlich nicht so =D Komisch, dass man Abneigungen gegen mathematische Ansätze haben kann.
Alena, danke für deine Antwort! Jetzt wissen wir den Weg und dass es auch funktioniert.
Gern! 🙂