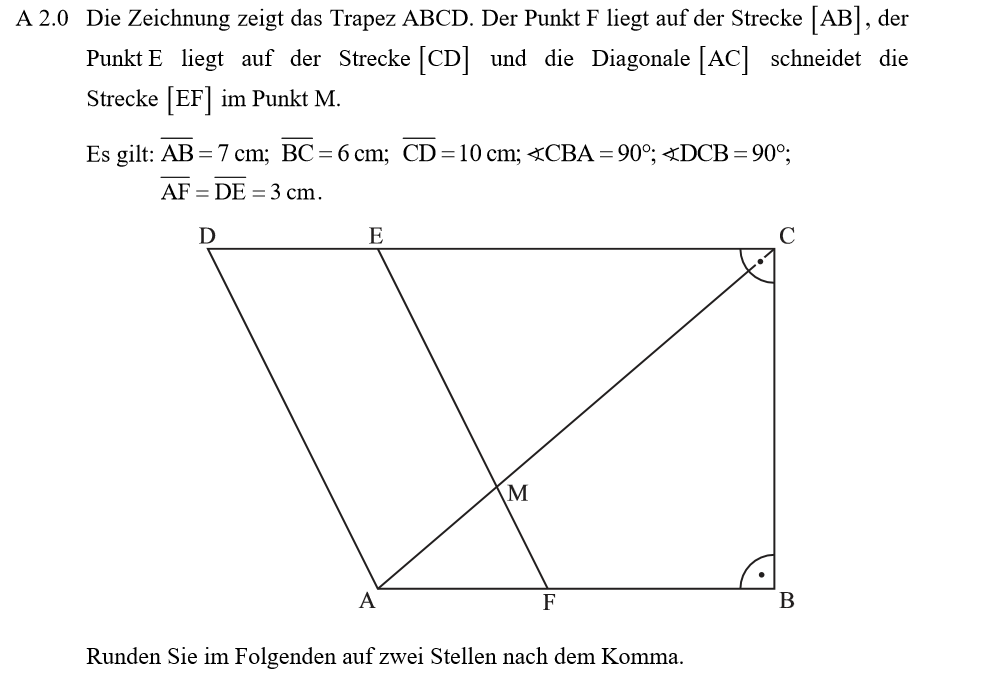
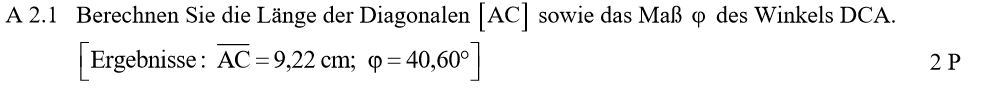
Lösung zu A2.1
\begin{align} &\overline{AC} \, mit \, dem \, Satz \, des \, Pythagoras: \\ \overline{AC}^2 &= \overline{AB}^2 + \overline{BC}^2 \\ &= 7^2 + 6^2 \\ \Rightarrow &\overline{AC} = 9,22 cm \\ \\ & \varphi \, mit \, dem \, Tangens: \\ tan(\angle DCA) &= \frac{\overline{AB}}{\overline{BC}} \\ tan(90° – \varphi) &= \frac{7}{6} \, \, \, | tan^{-1} \\ 90° – \varphi &= 49,40° \\ \Rightarrow &\varphi = 40,60° \end{align}
Zurück zum MAP-Hack:
Lösung zu A2.2
\begin{align} &\overline{MC} \, mit \, dem \, Vierstreckensatz: \\
\frac{\overline{MC}}{\overline{AC}} &= \frac{\overline{CD} – \overline{ED}}{\overline{CD}} \\
\\ \frac{\overline{MC}}{9,22} &= \frac{10-3}{10} \,\,\, | \cdot 9,22 \\ \\ \overline{MC} &= \frac{7}{10} \cdot 9,22 \\ \Rightarrow &\overline{MC} = 6,45 cm \end{align}
Zurück zum MAP-Hack:

Lösung zu A2.3

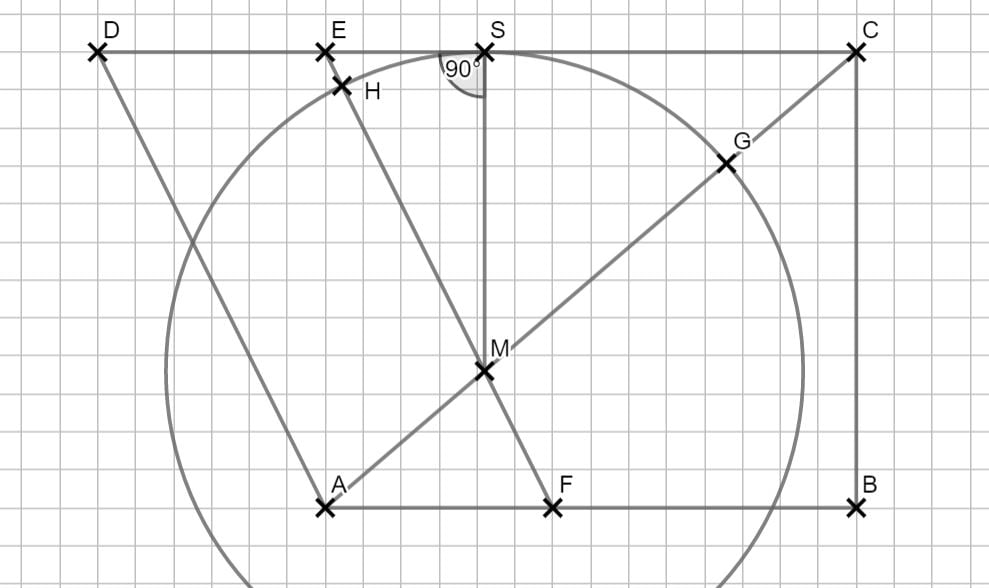
Zurück zum MAP-Hack:
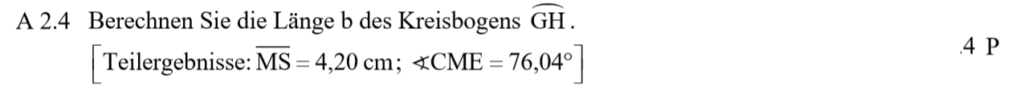
Lösung zu A2.4
Um die Bogenlänge (\( b = 2 \cdot r \cdot \pi \cdot \frac{\alpha}{360°} \) )zu berechnen, benötigst du den Radius \( r = \overline{MS} \) und den Winkel \(\alpha = \angle CME \). Dafür brauchst du \( \overline{ME} \).
\begin{align} & \overline{MS} \, mit \, dem \, Sinus: \\
sin(\varphi) &= \frac{\overline{MS}}{\overline{MC}} \\
sin(40,60°) &= \frac{\overline{MS}}{6,45} \,\,\, |\cdot 6,45 \\
\overline{MS} &=sin(40,60°) \cdot 6,45 \\
\Rightarrow &\overline{MS}= 4,20 \\ \\ &\overline{ME} \, mit \, dem \, Cosinussatz: \\ \overline{ME}^2 = (\overline{CD}-\overline{DE})^2 &+ \overline{MC}^2 – 2 \cdot (\overline{CD}-\overline{DE}) \cdot \overline{MC} \cdot cos(\varphi) \\ = (10 – 3)^2 &+ 6,45^2 – 2 \cdot (10 – 3) \cdot 6,45 \cdot cos(40,60°) \\ \Rightarrow &\overline{ME} = 4,69 cm \\ \\ & \angle CME \, mit \, dem \, Cosinussatz: \\ (\overline{CD} – \overline{DE})^2 = \overline{ME}^2 &+ \overline{MC}^2 – 2 \cdot \overline{ME} \cdot \overline{MC}\cdot cos(\angle CME) \\ cos(\angle CME) &= \frac{ \overline{ME}^2 + \overline{MC}^2 – (\overline{CD} – \overline{AB})^2}{2 \cdot \overline{ME} \cdot \overline{MC}} \\ &= \frac{4,69^2 + 6,45^2 – (10 – 3)^2}{2 \cdot 4,69 \cdot 6,45} \\ &= 0,241 \\ \Rightarrow &\angle CME = 76,04° \\ \\ &Berechnung \, der \, Bogenlaenge \, b: \\ b &= 2 \cdot \overline{MS} \cdot \pi \cdot \frac{\angle CME}{360°} \\&= 2 \cdot 4,20 \cdot \pi \cdot \frac{76,04°}{360°} \\ \Rightarrow &b=5,57cm \end{align}

Du hast eine Frage zu einer Teilaufgabe oder zur Lösung? Schreib‘ hier und du bekommst eine Antwort!