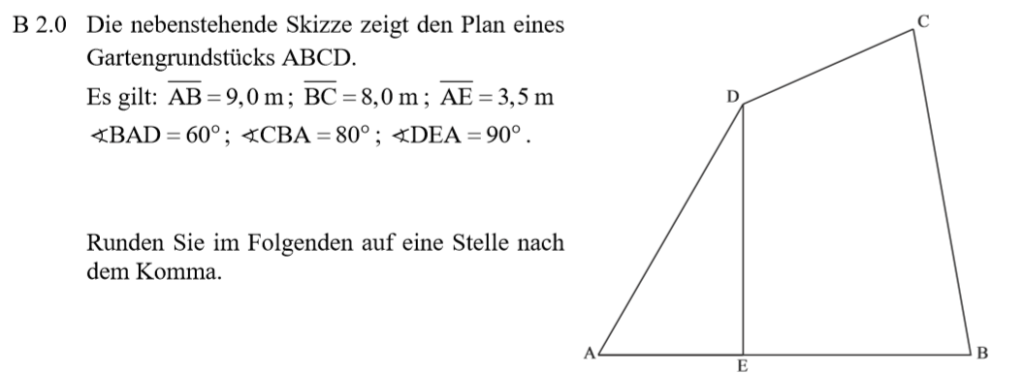
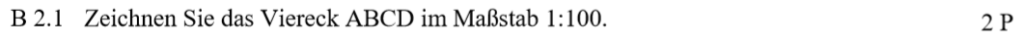
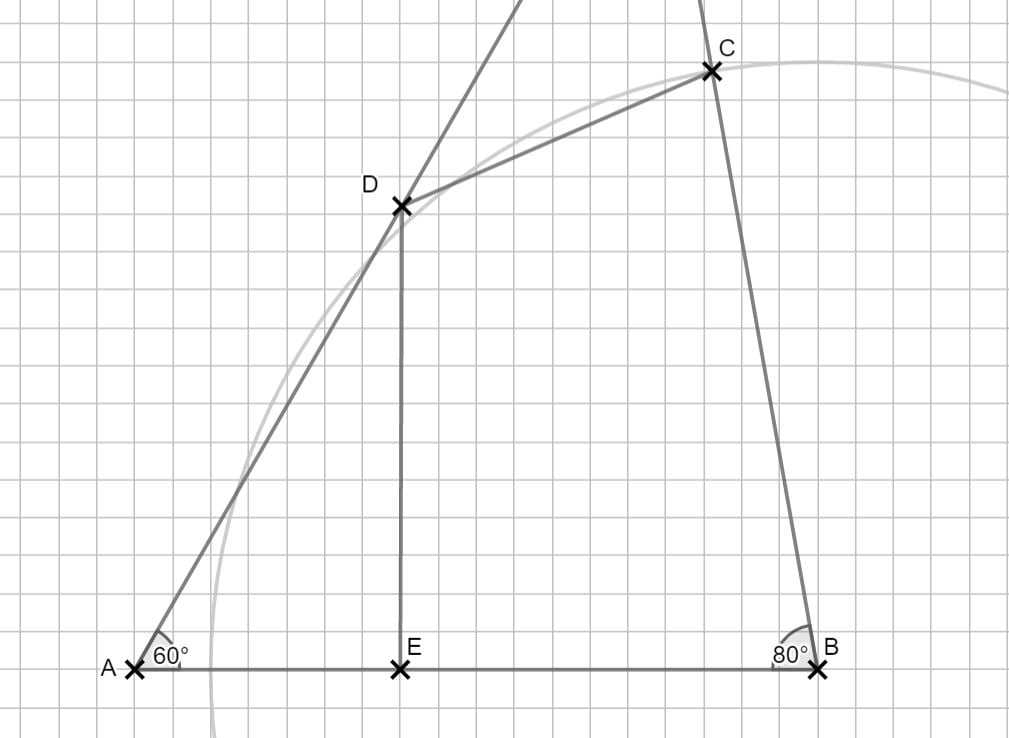
Lösung zu B2.1
Zurück zum MAP-Hack:

Lösung zu B2.2
\begin{align} &\overline{ED}\, mit \, dem \, Tangens: \\ tan(\angle BAD) &= \frac{\overline{ED}}{\overline{AE}} \,\,\, |\cdot \overline{AE} \\ \overline{ED}&= tan(\angle BAD) \cdot \overline{AE} \\ &= tan(60°) \cdot 3,5 \\ \Rightarrow &\overline{ED} = 6,1m \\ \\ &\overline{AD}\, mit \, dem \, Satz \, des \, Pythagoras: \\ \overline{AD}^2 &= \overline{ED}^2 + \overline{AE}^2 \\ &= 6,1^2 + 3,5^2 \\ \Rightarrow &\overline{AD} = 7,0 m \end{align}
Zurück zum MAP-Hack:

Lösung zu B2.3
\begin{align} &\overline{EC} \, dem \, umgeformten \, Cosinussatz: \\
\overline{EB} &= \overline{AB} – \overline{AE} \\ &= 9 – 3,5 \\
&= 5,5 \\
\\
\overline{EC}^2 &= \overline{BC}^2 + \overline{EB}^2 – 2 \cdot \overline{BC} \cdot \overline{EB} \cdot cos(\angle CBA) \\
&= 8^2 + 5,5^2 – 2 \cdot 8 \cdot 5,5 \cdot cos(80°) \\
\Rightarrow &\overline{EC} = 8,9 m \\
\\
&\angle CED \, über \, Sinussatz: \\
\frac{sin(\angle BEC)}{\overline{BC}} &= \frac{sin(\angle CBA)}{\overline{EC}} \,\,\, |\cdot \overline{BC} \\
sin(\angle BEC) &= \frac{sin(\angle CBA)}{\overline{EC}} \cdot \overline{BC} \\
&= \frac{sin(80°)}{8,9} \cdot 8 \\ \Rightarrow &\angle BEC = 62,3° \\
\\
\angle CED &= 90° – 62,3° \\ &= 27,7° \end{align}
Um den Flächeninhalt des Vierecks zu berechnen, zerteilst du es durch die Strecke [EC] in zwei Dreiecke und berechnest jeweils deren Flächeninhalte:
\begin{align} &A \, als \, Summe \, aus \, zwei \, Dreiecken: \\ \\ A_{BCE} &= 0,5 \cdot \overline{EB} \cdot \overline{BC} \cdot sin(\angle CBA) \\ &= 0,5 \cdot 5,5 \cdot 8 \cdot sin(80°) \\ \Rightarrow &A_{BCE}= 21,67 m^2 \\ \\ A_{CDE} &= 0,5 \cdot \overline{EC} \cdot \overline{ED} \cdot sin(\angle CED) \\ &= 0,5 \cdot 8,9 \cdot 6,1 \cdot sin(27,7°) \\ \Rightarrow &A_{CDE} = 12,62 m^2 \\
\\
A &= A_{BCE} + A_{CDE} \\ &= 21,67 + 12,62 \\ \Rightarrow A&=34,3m^2 \end{align}
Zurück zum MAP-Hack:

Lösung zu B2.4

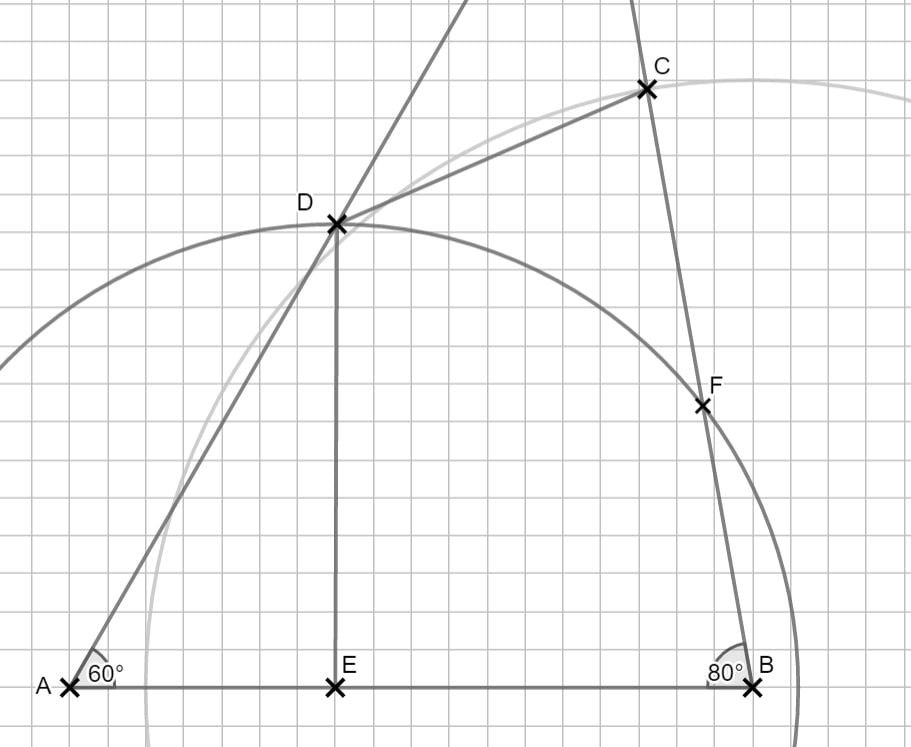
Zurück zum MAP-Hack:

Lösung zu B2.5
\begin{align} &\angle FED \, mit \, dem \, Sinussatz: \\
\angle FED &= 90° – \angle BEF \\
\\
\angle BED &= 180° – \angle CBE – \angle EFB \\
\\
\frac{sin(\angle EFB)}{\overline{EB}} &= \frac{sin(\angle CBA)}{\overline{ED}} \\
\frac{sin(\angle EFB)}{5,5} &= \frac{sin(80°)}{6,1} \,\,\, |\cdot 5,5 \\
sin(\angle EFB) &= \frac{sin(80°)}{6,1} \cdot 5,5 \\ \Rightarrow &\angle EFB = 62,6° \\
\Rightarrow &\angle BEF = 37,4° \\
\Rightarrow &\angle FED = 52,6° \\ \\ &Berechnung \, der \, Bogenlänge\, b: \\ b &= 2 \cdot \overline{ED} \cdot \pi \cdot \frac{\angle FED}{360°} \\ &= 2 \cdot 6,1 \cdot \pi \cdot \frac{52,6°}{360°} \\ \Rightarrow &b = 5,6 m \\ \\ &\overline{CD} \, mit \, dem \, Cosinussatz: \\ \overline{CD}^2 &= \overline{ED}^2 + \overline{EC}^2 – 2 \cdot \overline{ED} \cdot \overline{EC}^2 \cdot cos(\angle CED) \\&= 6,1^2 + 8,9^2 – 2 \cdot 6,1 \cdot 8,9 \cdot cos(27,7°) \\ \Rightarrow &\overline{CD} = 4,5 m \\ \\ &l \, durch \, Addition: \\ l &= b + \overline{CD}\\ &= 5,6 + 4,5 \\ \Rightarrow &l = 10,1 m \end{align}
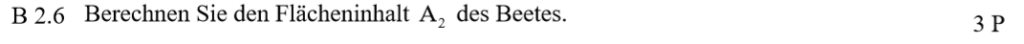
Lösung zu B2.6
Die gesuchte Fläche setzt sicht aus dem Drachenviereck und dem Kreissektor zusammen. Wie in 1.5 zerlegst du den Drachen in zwei Dreiecke und berechnest deren Flächen einzeln. Für den Flächeninhalt des Sektors benötigst du den den Winkel FEC:
Weil die Rechnung zu lang wird, werden die Formeln der Flächeninhalte untereinander geschrieben. Es ist aber eine Rechnung.
\begin{align} &\angle FEC \, als \, Differenz: \\ &\angle FEC = 62,3° – 37,4° = 24,9° \\ \\ &A \, durch \, Zusammensetzen: \\ A &= A_{EFC} + A_{EDC} – A_{Sektor} \\ = &0,5 \cdot \overline{EF} \cdot \overline{EC}\cdot sin(\angle FEC) \\ &+ 0,5 \cdot \overline{EC} \cdot \overline{ED} \cdot sin(\angle CED) \\ &- \overline{ED}^2 \cdot \pi \cdot \frac{\angle FED}{360°} \\ \\ = &0,5 \cdot 6,1 \cdot 8,9 \cdot sin(24,9°) \\ &+0,5 \cdot 8,9\cdot 6,1 \cdot sin(27,7°) \\ &- 6,1^2 \cdot \pi \cdot \frac{52,6°}{360°}\\ \Rightarrow & A = 7,0 m^2 \end{align}
