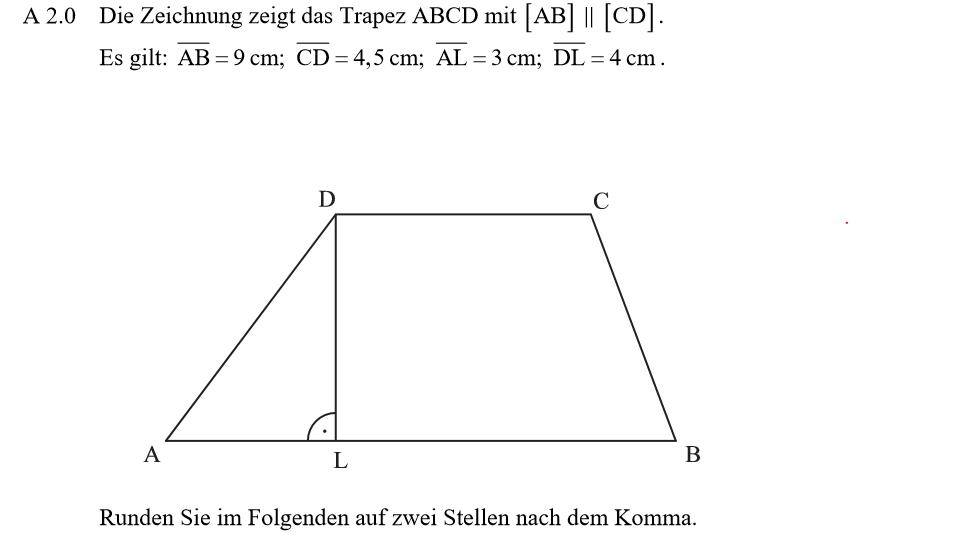
Lösung zu A2.1
Delta kann nicht sofort bestimmt werden! Delta setzt sich aus dem rechten Winkel und dem Winkel ADL zusammen. Letzteren musst du bestimmen.
\begin{align} &\angle \text{ ADL mit dem Tangens:} \\
tan(\angle ADL) &= \frac{\, \overline{AL} \,}{\, \overline{DL}\,} \\ &= \frac{\, 3\, }{\, 4 \,} \\
\Rightarrow &\angle ADL = 36,87° \\ \\ &\text{Berechnung von }\delta: \\
\delta &= 90° + \angle ADL \\
&= 90° + 36,87° \\
\Rightarrow &\delta = 126,87° \end{align}
Zurück zum MAP-Hack:
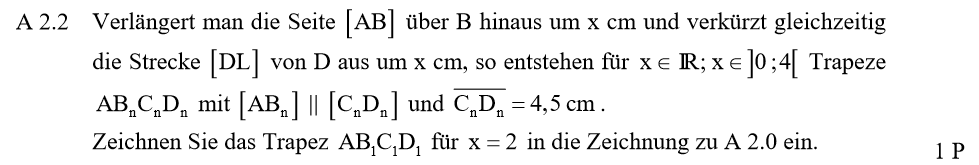
Lösung zu A2.2
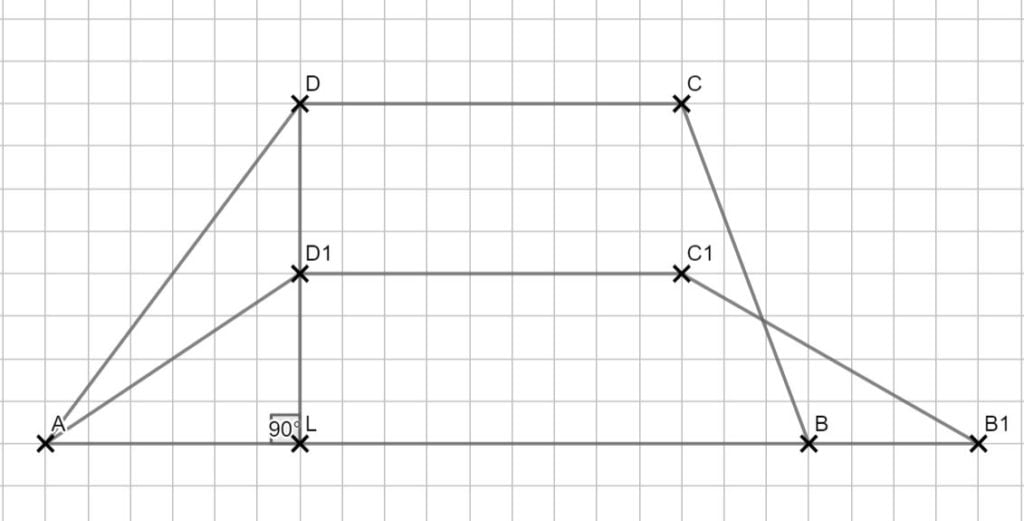
Zurück zum MAP-Hack:
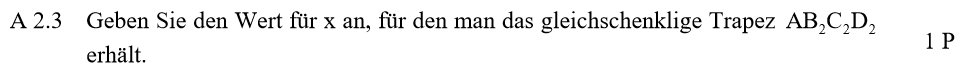
Lösung zu A2.3
Wirft man das Lot von C auf AB, dann nennen wir den Lotfußpunkt rechts L*. Das Trapez ist gleichschenklig, wenn die Länge der Strecken [AL] und [BL*] gleich sind. Weil die \(\overline{AL} = 3\) gilt, muss das auch für \( \overline{BL‘} \) gelten.
Damit kannst du anfangen:
\begin{align} \overline{B_2 L‘} &= \overline{AL} + x \\ &= \overline{AB} – \overline{AL}- \overline{CD} + x \\ &= 9 – 3 – 4,5 + x \\ \Rightarrow &\overline{B_2 L‘} = (1,5 + x ) cm \end{align}
Dass 1,5 + x gleich 3 ist, muss x = 1,5 gelten und damit hast du die Antwort gefunden.
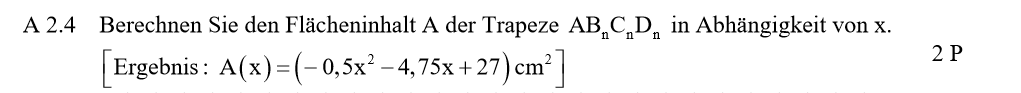
Lösung zu A2.4
In die Flächenformel des Trapezes (\( A = 0,5 \cdot (a + c ) \cdot h\)) kannst du direkt einsetzen:
\begin{align} A &= 0,5 \cdot (\overline{AB_n} + \overline{C_n D_n}) \cdot \overline{D_n L} \\
&= 0,5 \cdot [(9+x) + 4,5] \cdot (4 – x) \\
&= 0,5 \cdot (13,5 + x) \cdot (4- x) \\
&= 0,5 \cdot (54 – 13,5x + 4x – x^2) \\
&= 0,5 \cdot (-x^2 – 9,5x + 54) \\
\Rightarrow A(x) &= (-0,5x^2 – 4,75x + 27) cm^2 \end{align}

Lösung zu A2.5
Setzte die Formel aus 2.4 mit 28 gleich und löse die Gleichung dann mit deinem Taschenrechner:
\begin{align} A(x) &= 28 \,\,\, |-28\\
-0,5x^2 – 4,75x – 1 &= 0 \\
\Rightarrow &\text{GTR:} \, x = -0,22 \, \lor \, x = -9,28 \end{align}
Beide Wete sind kleiner als Null und damit nicht für x erlaubt. Es gibt also kein Trapez mit dem gesuchten Flächeninhalt.
