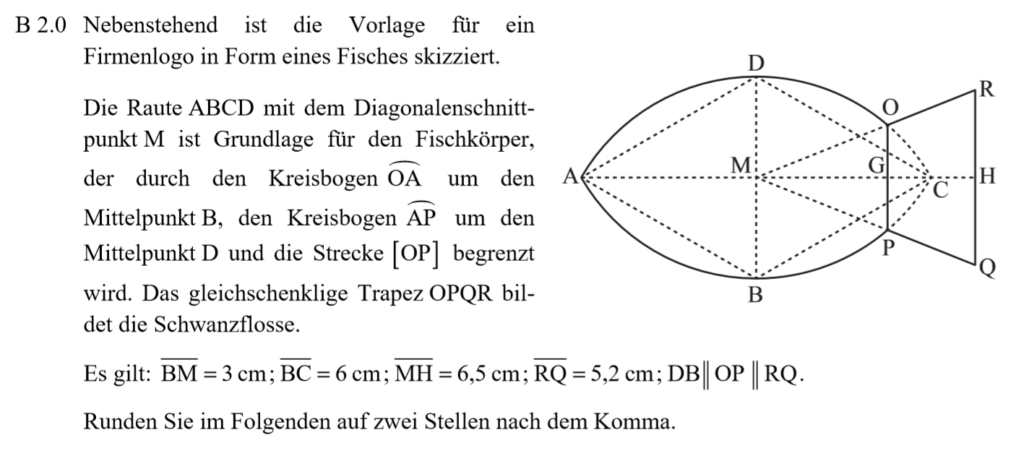

Lösung zu B2.1
\begin{align}& \overline{CM} \, mit \, dem \, Satz \, des \, Pythagoras: \\
\overline{BC}^2 &= \overline{CM}^2 + \overline{BM}^2 \, \, |-\overline{BM}^2 \\
\overline{CM}^2 &= \overline{BC}^2 – \overline{BM}^2 \\
&= 6^2 – 3^2 \\ \Rightarrow &\overline{CM} = 5,20 cm \end{align}
Weil die Dreieck ABD und BCD gleichseitig sind, folgt für \( \beta = 2 \cdot 60° = 120° \).
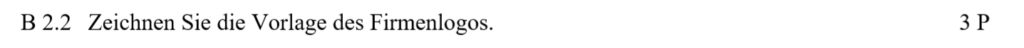
Lösung zu B2.2
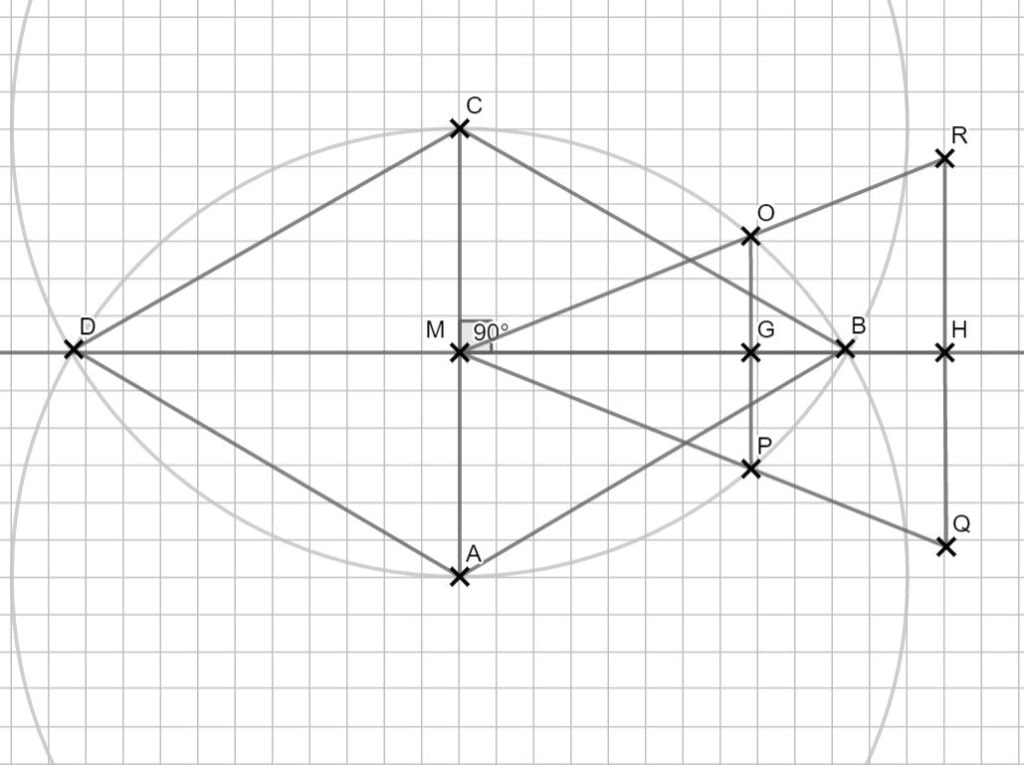
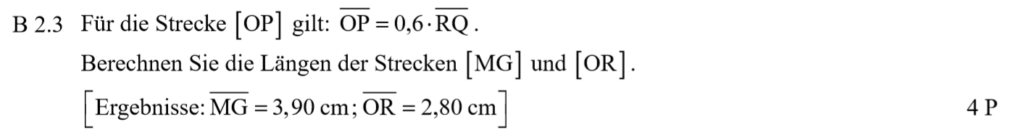
Lösung zu B2.3
\begin{align} & \overline{OP} \, mit \, angegebener \, Formel: \\
\overline{OP} &= 0,6 \cdot 5,2 = 3,12 cm \\
\\
& \overline{MG} \, mit \, Vierstreckensatz: \\ \
frac{\overline{MG}}{\overline{MH}} &= \frac{\overline{OP}}{\overline{RQ}} \\
\frac{\overline{MG}}{6,5} &= \frac{3,12}{5,2} \, \, \, |\cdot 6,5 \\
\overline{MG} &= \frac{3,12}{5,2} \cdot 6,5 \\
\Rightarrow & \overline{MH}= 3,90 cm \\
\\
& \overline{MR} \, mit \, dem \, Satz \, des \, Pythagoras: \\
\overline{MR}^2 &= \overline{MH}^2 + (0,5 \cdot \overline{RQ})^2 \\
&= 6,5^2 + (0,5 \cdot 5,2)^2 \\
\Rightarrow \overline{MR} &= 7,00 cm \\
\\
&\overline{MO} \, mit \, Vierstreckensatz: \\
\frac{\overline{MO}}{\overline{MR}} &= \frac{\overline{MG}}{\overline{MH}} \\
\frac{\overline{MO}}{7,00} &= \frac{3,90}{6,5} \,\, \, |\cdot 7,00 \\
\overline{MO} &= \frac{3,90}{6,5} \cdot 7,00 \\ \Rightarrow &\overline{MO} = 4,20 \\
\\
&\overline{OR} \, als \, Differenz: \\
\overline{OR} &= \overline{MR} – \overline{MO} \\
&= 7,00 – 4,20 \\
\Rightarrow &\overline{OR} = 2,80 cm. \end{align}
Zurück zum MAP-Hack:

Lösung zu B2.4
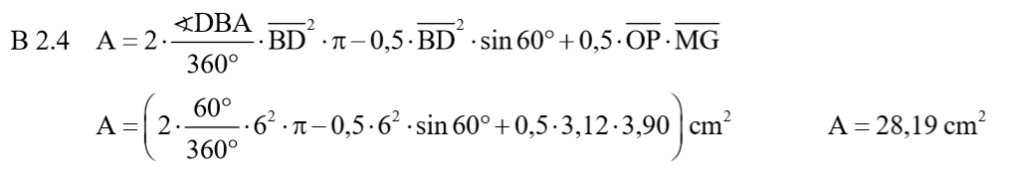
Zurück zum MAP-Hack:

Lösung zu B2.5
Weil die Figur symmetrisch ist, kannst du den oberen Kreisbogen von A zu O berechnen und dann verdoppeln. Die Länge der Strecke \(\overline{OR} = 2,80 cm \) kommt doppelt vor und dann fehlt nurnoch \(\overline{RQ} = 5,2 cm\), dann bist du einmal außenrum.
\begin{align} &Ziel: u = 2 \cdot \frac{\angle OBA}{360°} \cdot 2 \overline{BC} \cdot \pi + 2 \cdot \overline{OR} + \overline{RQ} \end{align}
Zum Einsetzen brauchst du nurnoch den Winkel des Kreisbogens OBA, der sich aus den Winkeln OBD und DBA zusammensetzt. Der Winkel DBA hat das Maß 60°, weil das Dreieck gleichseitig ist.
\begin{align} & \angle OBM \, mit \, dem \, umgeformten \, Cosinussatz: \\ \overline{MO}^2 &= \overline{BO}^2 + \overline{BM}^2 – 2 \cdot \overline{BO} \cdot \overline{BM} \cdot cos(\angle OBM) \\ cos(\angle OBM) &= \frac{\overline{BO}^2 + \overline{BM}^2 – \overline{MO^2}}{2 \cdot \overline{BO} \cdot \overline{BM}} \\ &= \frac{6^2 +3^2 – 4,2^2}{2 \cdot 6 \cdot 3} \\ \Rightarrow & \angle OBM = 40,54° \\ \\ & \angle OBA \, mit \, Addition: \\ \angle OBA &= \angle OBM + \angle DBA \\ &= 40,54° + 60° \\ \Rightarrow &\angle OBA = 100,54° \\ \\ &Einsetzen \, in \, die\, Umfangsformel: \\ u &= 2 \cdot \frac{\angle OBA}{360°} \cdot 2 \overline{BC} \cdot \pi + 2 \cdot \overline{OR} + \overline{RQ} \\ &= 2 \cdot \frac{100,54°}{360°} \cdot 2 \cdot 6 \cdot \pi + 2 \cdot 2,80 + 5,2 \\ \Rightarrow &u = 31,86 cm \end{align}

Lösung zu B2.6
Es werden \( 3 \cdot 31,86 = 95,58 cm \) Faden benötigt. Teilst du die 500m Faden pro Rolle durch diesen Wert, erhälst du die Anzahl von Firmelnlogos:
\begin{align} Anzahl &= l_{Rolle} : l_{Logo} \\ &= 500 \cdot 100 : 95,58 \\ \Rightarrow &Anzahl = 523,12 \end{align}
Es können höchstens 523 Firmenlogos hergestellt werden.
