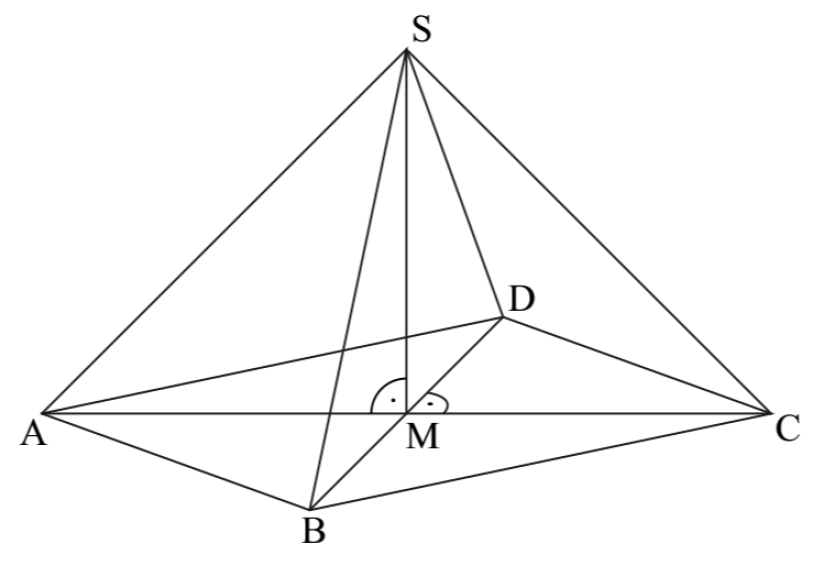
1.0 Die nebenstehende Skizze zeigt ein Schrägbild der Pyramide ABCDS, deren Grundfläche die Raute ABCD mit dem Diagonalenschnittpunkt M ist.
Die Spitze S der Pyramide ABCDS liegt senkrecht über dem Mittelpunkt M.
Es gilt:
\( |\overline{AC}| = 12 cm; |\overline{BD}|= 8 cm; |\overline{MS}| = 9 cm \)
Runden Sie im Folgenden auf zwei Stellen nach dem Komma.
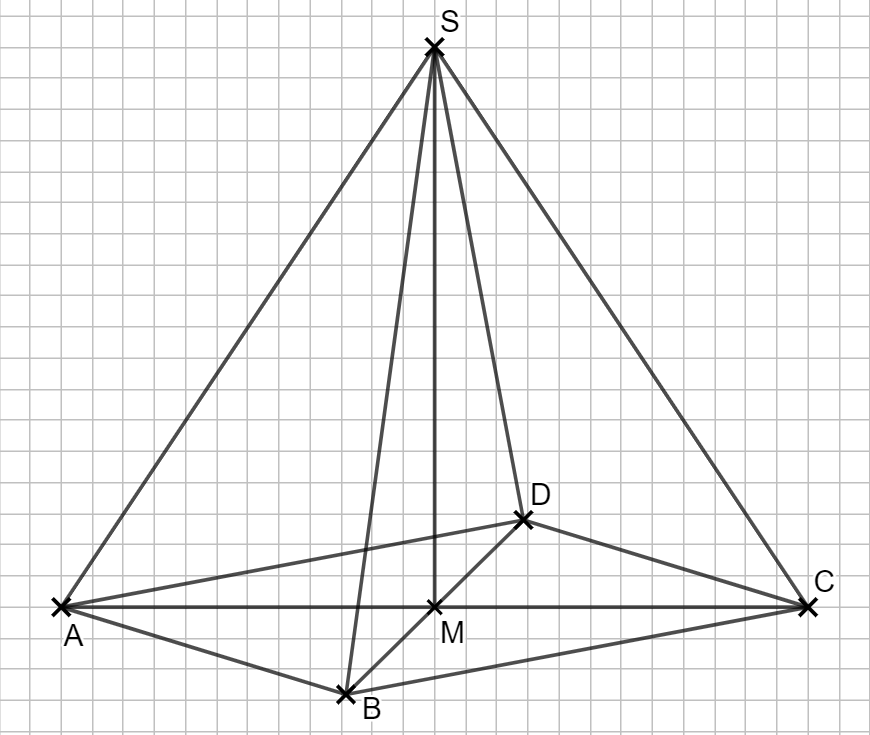
1.1 Zeichnen Sie das Schrägbild der Pyramide ABCDS, wobei die Strecke \(\overline{AC}\) auf der Schrägbildachse und der Punkt A links von Punkt C liegen soll.
Für die Zeichnung gilt: q = 0,5 ; ω = 45°.
Lösung zu 1.1
1.2 Bestimmen Sie rechnerisch die Länge der Strecke \( \overline{AS} \) und das Maß des Winkels ∢ CAS.
[Ergebnis: \( \angle CAS = 56,31° \) ]
Lösung zu 1.2
\begin{align} &|\overline{AS}|\text{ mit dem Satz des Pythagoras:}\\
|\overline{AS}|^2 &= |\overline{AM}|^2 + |\overline{MS}|^2 \\
&= 6^2 + 9^2 \,\,\, |\sqrt{}\\
&\Rightarrow \overline{AS} = 10,82 \text{cm}\\
\\
&\angle CAS \text{ mit dem Tangens:}\\
tan(\angle CAS) &= \frac{|\overline{MS}|}{|\overline{AM}|}\\
&= \frac{9}{6} \,\,\, |tan^{-1}\\
&\Rightarrow \angle CAS = 56,31° \end{align}
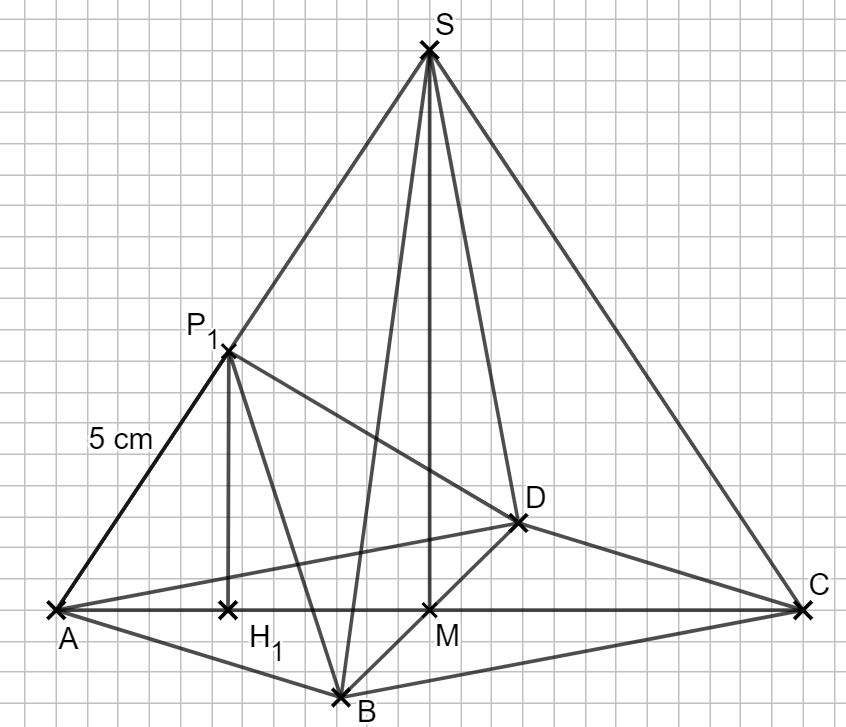
1.3 Für Punkte \(P_n \) auf der Strecke \( \overline{AS} \) gilt: \(|\overline{AP_n(x)}| = x\)cm mit \( x \in \mathbb{R} \) und \(0 < x ≤ 10,82 \). Die Punkte \( P_n \) sind Spitzen von Pyramiden ABDPn.
Zeichnen Sie die Pyramide ABDP1 und die dazugehörige Höhe \(\overline{H_1 P_1 } \) mit dem Höhenfußpunkt H1 auf [AM] für x = 5 in das Schrägbild zu 1.1 ein.
Lösung zu 1.3
1.4 Bestimmen Sie das Volumen der Pyramide ABDP1:
[Ersatzergebnis: \( |\overline{H_1P_1}| = 4,16 cm \) ]
Lösung zu 1.4
Für die Flächenformel der Pyramide brauchst du deren Höhe \( H_1 P_1 \). Das über diese Strecke der Lösungsweg führt, zeigt dir auch das Ersatzergebnis.
\begin{align} &|\overline{H_1 P_1}| \text{ mit dem Sinus:}\\
sin(\angle CAS) &= \frac{|\overline{H_1 P_1}|}{|\overline{AP_1}|}\\
sin( 56,31°) &= \frac{|\overline{H_1 P_1}|}{5} \,\,\, |\cdot 5 \\
&\Rightarrow |\overline{H_1 P_1}| = sin( 56,31°) \cdot 5 = 4,16 \text{cm}\\
\\
&\text{Einsetzen in die Volumenformel:} \\
V_{ABDP_1} &= \frac{1}{3} \cdot A_{ABD} \cdot |\overline{H_1 P_1}| \\
&= \frac{1}{3} \cdot \frac{1}{2} \cdot |\overline{BD}| \cdot |\overline{AM}| \cdot |\overline{H_1 P_1}| \\
&= \frac{1}{3} \cdot \frac{1}{2} \cdot 8 \cdot 6 \cdot 4,16 \\
&\Rightarrow V_{ABDP_1} = 33,28 \text{cm}^3 \end{align}
1.5 Bestimmen Sie den prozentualen Anteil des Volumens der Pyramide ABDP1 an der Pyramide ABCDS.
Lösung zu 1.5
Zuerst berechest du das Volumen der großen Pyramide ABCDS, um dann den prozentualen Anteil auszurechnen.
\begin{align} V_{ABCDS} &= \frac{1}{3} \cdot \frac{1}{2} \cdot |\overline{BD}| \cdot |\overline{MS}| \\
&= \frac{1}{3} \cdot \frac{1}{2} \cdot 12 \cdot 8 \cdot 9 \\
&\Rightarrow V_{ABCDS} = 144 \text{cm}^3 \\
\\
p &= \frac{V_{ABDP_1}}{V_{ABCDS}} \cdot 100 \% = \frac{33,28}{144} \cdot 100 \% \\
&\Rightarrow p = 23,11 \% \end{align}
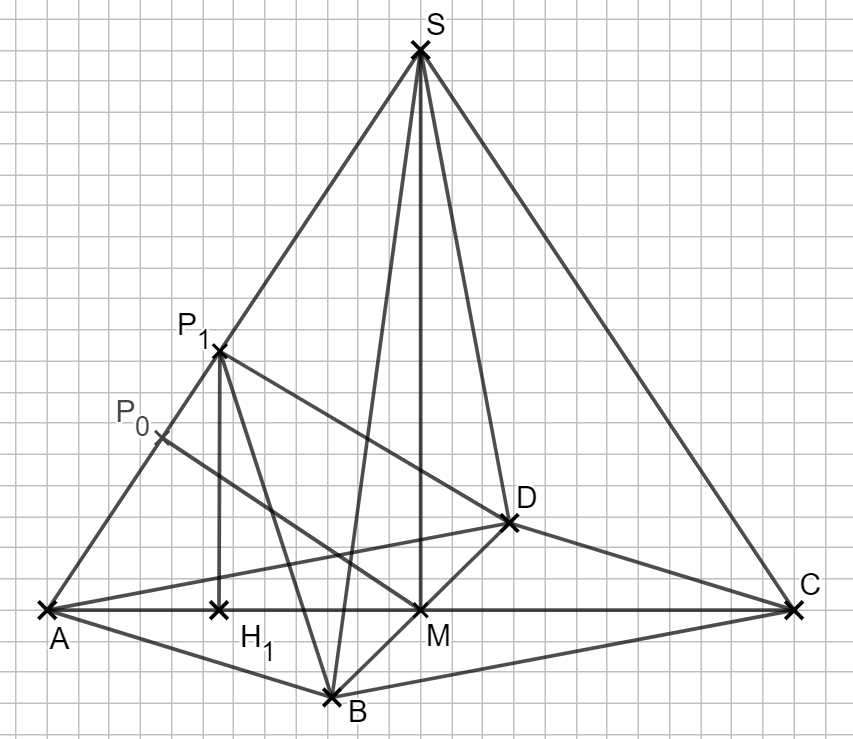
1.6 Der Punkt P0 hat die kürzeste Entfernung zu M. Zeichnen Sie den Punkt P0 ins Schrägbild von 1.1 ein und bestimmen Sie den zugehörigen Wert von x.
Begründen Sie, dass es unter den Dreiecken BDPn kein Dreieck mit Flächeninhalt 18 cm² gibt.
Lösung zu 1.6
Einzeichnen von \( \overline{MP_0} \) über den rechten Winkel bei \( P_0\).
Weil der Punkt P die kürzeste Entfernung hat, gelten die Regeln des Abstands. Die Strecke steht in einem rechten Winkel, also darfst du auch mit Sinus, Cosinus usw. rechnen.
\begin{align} |\overline{MP_0}| \text{ mit dem Sinus:}\\
sin(\angle CAS) &= \frac{|\overline{MP_0}|}{|\overline{AP}|} \\
sin(56,31°) &= \frac{|\overline{MP_0}|}{6} \,\,\, |\cdot 6 \\
&\Rightarrow |\overline{MP_0}| = sin(56,31°) \cdot 6 = 4,99 \text{cm} \end{align}
Weil die Grundseite des Dreiecks \( BDP_0\) durch B und D fest ist, verändert sich der Flächeninhalt nur durch die Höhe, welche \( \overline{MP}\) ist. Die kürzeste Höhe ist \(MP_0 \) und damit entsteht für diese Höhe auch das kleineste Dreieck.
\begin{align}
A_{min} &= 0,5 \cdot |\overline{MP_0}| \cdot |\overline{BD}| \\
&= 19,95 \text{cm}^2 \end{align}
Das kleinste Dreieck hat einen Flächeninhalt von 19,95 cm², also gibt es kein kleineres Dreieck – auch keines mit 18 cm².