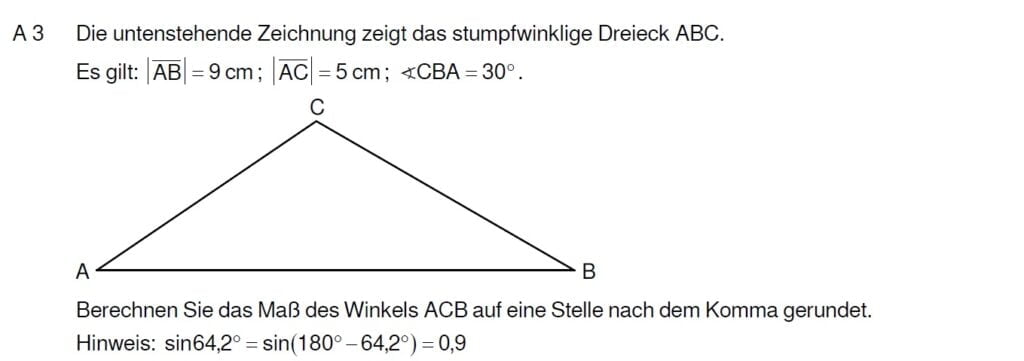
Lösung zu A3
Das Dreieck hat keinen rechten Winkel, also bleibt noch Sinus-Satz oder Cosinus-Satz übrig. Wie kommst du zum Ziel?
\begin{align} &\text{Ansatz mit dem Sinus-Satz:}\\
\frac{sin(\angle ACB)}{|\overline{AB}|} &= \frac{sin(\angle CBA)}{|\overline{AC}|} \\
\frac{sin(\angle ACB)}{9} &= \frac{sin(30°)}{5} \\
\\
sin(30°) &= 0,5 \,\,\,\, \text{siehe Tabelle in der Formelsammlung}\\
\\
\frac{sin(\angle ACB)}{9} &= \frac{0,5}{5} \,\,\, |\cdot 9\\
sin(\angle ACB) &= \frac{0,5}{5} \cdot 9\\
sin(\angle ACB) &= \frac{1}{10} \cdot 9 = 0,9\\
\Rightarrow \angle ACB = 64,2° \lor 180° – 64,2° = 115,8° \end{align}
Es muss der größere Winkel gewählt werden, da in der Aufgabe steht, dass ABC stumpfwinklig ist. Ein Winkel muss also größer als 90° sein. Wäre ACB 64,2°, wäre der letzte Winkel 180° – 64,2° – 30° < 90° und die Vorraussetzung wäre nicht erfüllt.
