1.0 Niger ist ein Staat in Westafrika. Zu Beginn des Jahres 2010 lebten dort etwas 15,5 Millionen Menschen. Unter der Annahme einer gleichbleibenden jährlichen Wahstumsrate lässt sich die Einwohnerzahl y Millionen nach x Jahren näherunsweise durch die Funktion f mit der Gleichung \( y = 15,5 \cdot 1,035^x \) mit \( \mathbb{R}^{0+} \text{ x } \mathbb{R}^{0+} \).
1.1 Ergänzen Sie die Wertetabelle auf eine Stelle nach dem Komma gerundet. Zeichnen Sie sodann den Graphen f in das Koordinatensystem.
| x | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
| y |
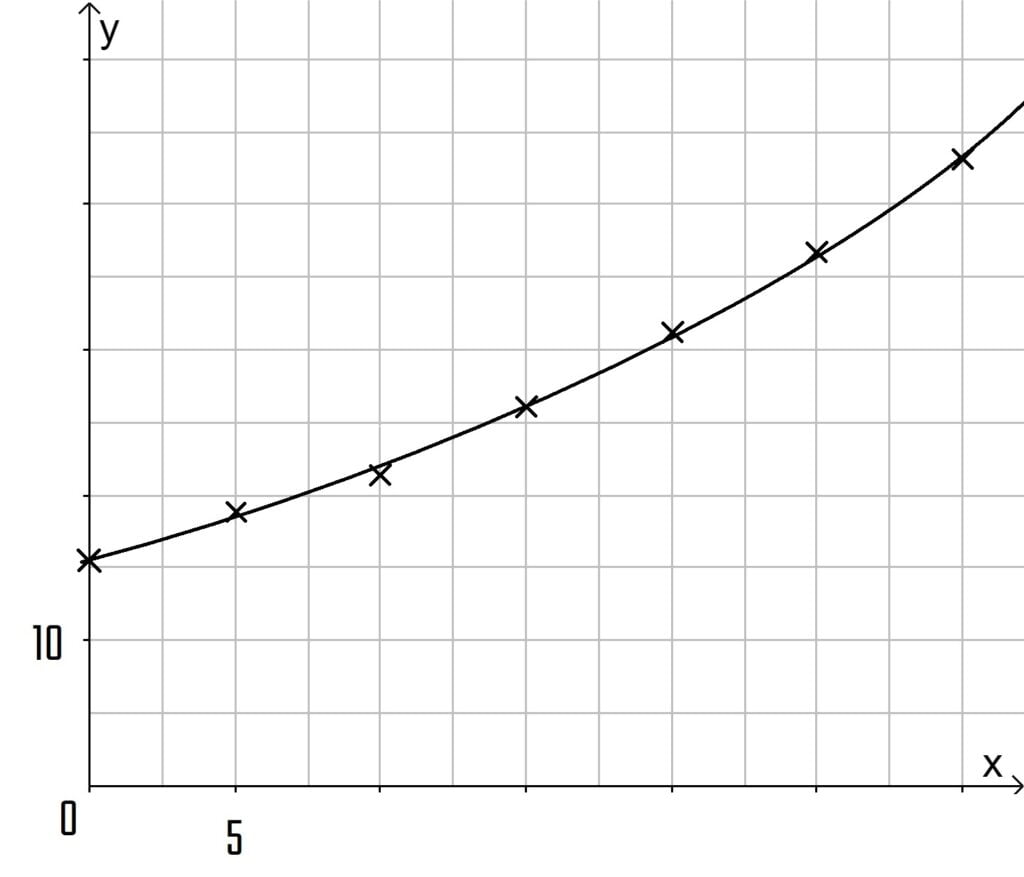
Lösung zu 1.1
| x | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
| y | 15,5 | 18,4 | 21,9 | 26,0 | 30,8 | 36,6 | 43,5 |
1.2 Um wie viel Prozent wächst nach dieser Annahme ab dem Jahresbeginn 2010 die Einwohnerzahl in Niger jährlich?
Sie wächst um ________ % .
Lösung zu 1.2
1,035 sind 0,035 mehr als 1.
Das sind \( 0,035 \cdot 100 \% = 3,5\% \)
1.3 Berechnen Sie auf Millionen gerundet, wie viele Einwohner Niger bei gleichbleibender jährlicher Zuwachsrate zu Beginn des Jahres 2064 haben würde.
Lösung zu 1.3
Bis zum Jahr 2064 vergehen \( 2064 – 2010 = 54 \) Jahre.
\( f(54) = 15,5 \cdot 1,035^{54} = 99,3 \).
Es leben 99,3 Millionen Menschen dort.
1.4 Bestimmen Sie rechnerisch, nach wie vielen Jahren die Einwohnerzahl von Niger 25 Millionen betragen würde.
Lösung zu 1.4
\begin{align} f(x) &= 25 \\
15,5 \cdot 1,035^{x} &= 25 \,\,\, |:15,5 \\
1,035^x &= 1,61 \,\,\, | log_{1,035}() \\
x &= 13,8 \text{Jahre} \end{align}
