

Lösung zu B1.1
Es sind zwei Punkte geben, also musst du ein Gleichungssystem aufstellen.
Es sind zwei Punkte gegeben, also stellten wir zwei Gleichungen auf:
\begin{align}
(I) \, y &= -0,2x^2 + bx + c \,\,\, \text{ mit }P(-2|2,8)\\
&\land (II) \, y = -0,2x^2 +bx + c \,\,\, \text{ mit }Q(7|1)\\
\\
(I) \, 2,8 & = -0,2 \cdot (-2)^2 + b \cdot (-2) + c \\
&\land (II) \, 1 = -0,2\cdot 7^2 + b \cdot 7 + c \\
\\
(I) \, 2,8 &= -0,8 -2b + c \,\,\, |+0,8 \\
&\land (II)\, 1 = -9,8 + 7b + c \,\,\, |+9,8 \\
\\
(I) 3,6 &= -2b + c \\
&(II) 10,8 = 7b + c \\
\\
\Rightarrow >R \Rightarrow Mode A \Rightarrow 1 \Rightarrow 2 \\
\Rightarrow b &= 0,8 ; c = 5,2\\
\\
y &= -0,2x^2 + 0,8x + 5,2 \end{align}
Hier geht es zur allgemeinen Erklärung:

Lösung zu B1.2
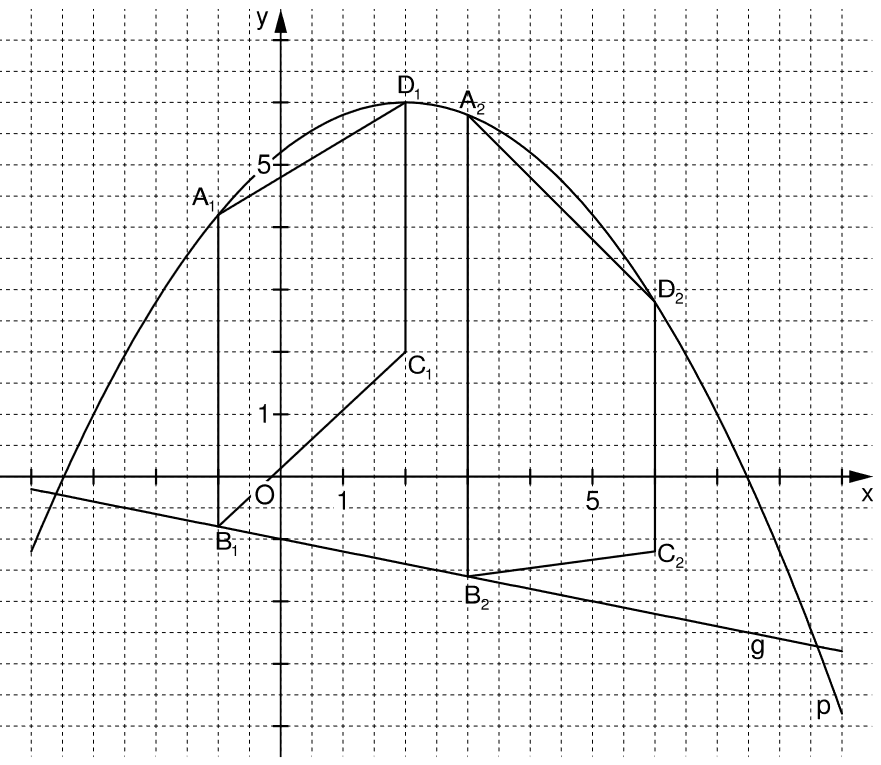
Selbe Abszisse heißt, dass sie übereinander liegen. Eine um drei größere Abszisse, dass der Punkt drei LE weiter rechts ist.
Einzeichnen der Trapeze. Siehe 1.1
Hier geht es zur allgemeinen Erklärung:

Lösung zu B1.3
In der Flächenformel sind a und c die beiden parallelen Seiten des Trapezes.
Hier kannst du oben – unten verwenden. Die Höhe des Trapezes ist der Unterschied in der Abszisse.
Dieser Unterschied ist immer gleich.
Für den Flächeninhalt des Trapezes benötigst du die Längen der parallelen Strecken (Hier \( \overline{AB} \text{ und } \overline{CD} \) und die Höhe.
Die Höhe ist der Abstand der Stecken \( \overline{AB} \text{ und } \overline{CD} \). Weil die Abszisse von C und D laut Angabe immer um 3 größer ist, ist die Höhe des Trapezes also 3.
Die Länge der Strecke \( \overline{AB} \) berechnet man durch „Oben – unten“:
\begin{align} &|\overline{AB}| \text{ durch „oben-unten“:}\\
|\overline{A_n B_n}|(x) &= y_{parabe}l – y_{gerade} \\
&= -0,2x^2 +0,8x + 5,2 – (-0,2x -1) \\
&= -0,2x^2 +0,8x + 5,2 + 0,2x +1 \\
\Rightarrow |\overline{A_n B_n}| = -0,2x^2 + x + 6,2 \\
\\
&A(x) \text{mit der Flächenformel des Trapezes:}\\
A(x) &= \frac{1}{2} \cdot ( |\overline{A_n B_n}| + |\overline{C_n D_n}| ) \cdot h \\
&= 0,5 \cdot (-0,2x^2 +x + 6,2 + 4) \cdot 3 \\
&= 1,5 \cdot (-0,2x^2 +x + 10,2) \\
\Rightarrow &A(x) = -0,3x^2 + 1,5x + 15,3 \\
\\
&\text{Bestimmung des Extremwerts mit dem GTR:}\\
&\Rightarrow GTR \Rightarrow Mode A \Rightarrow 2 \Rightarrow 2 \\
&A_max = 17,18 FE \text{ für } x = 2,5 \end{align}
Hier geht es zur allgemeinen Erklärung:

Lösung zu B1.4
Stelle mit dem Ersatzergebnis aus 1.3 eine Gleichung auf, indem du es mit 16,5 gleichsetzt.
Um eine Gleichung aufzustellen, setzte einfach den Flächenterm aus 1.3 mit dem gesuchten Wert 16,5 gleich.
\begin{align} &\text{Gleichsetzen mit dem Term aus 1.3}\\
A(x) = 16,5 \\
-0,3x^2 + 1,5x + 15,3 &= 16,5 \,\,\, |-16,5 \\
-0,3x^2 + 1,5x – 1,2 &= 0 \\
&\Rightarrow GTR \Rightarrow Mode A \Rightarrow 2 \Rightarrow 2 \\
x_1 = 1 \, \lor \, x_2 = 4 \end{align}
Hier geht es zur allgemeinen Erklärung:
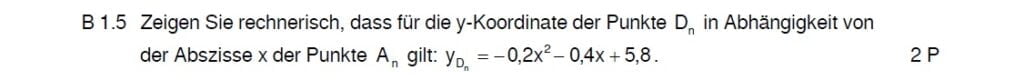
Lösung zu B1.5
Ersetze im Funktionsterm jedes x durch (x+3) und vereinfache.
Weil die Abszisse x von D immer um 3 größer ist, setzt du im Funktionsterm für jedes x ein (x+3) ein und vereinfachst. Ja, das ist schon alles.
\begin{align} y_D &= -0,2 \cdot (x + 3) ^2 + 0,8 \cdot (x + 3) + 5,2 \\
&= -0,2 \cdot (x^2 + 6x + 9) + 0,8x + 2,4 + 5,2 \\
&= -0,2x^2 – 1,2x – 1,8 + 0,8x + 2,4 + 5,2 \\
\Rightarrow &y = -0,2x^2 – 0,4x + 5,8 \end{align}

Lösung zu B1.6
Irgendetwas muss es mit den Koordinaten von D zu tun haben, denn wofür gäbe es sonst das Ersatzergebnis in 1.5?
Wenn \( \overline{AD} \) parallel zur x-Achse ist, dann liegen A und D auf derselben Höhe, haben also den selben y-Wert.
Der y-Wert von A ist gleich dem Parabel-Term und der y-Wert von D kann durch den Term aus 1.5 ersetzt werden. So lässt sich eine Gleichung aufstellen.
\begin{align} y_A &= y_D \\
-0,2x^2 + 0,8x + 5,2 &= -0,2x^2 – 0,4x + 5,8 \,\,\, |+0,2x^2 + 0,4x – 5,8 \\
0 \cdot x^2 + 1,2x – 0,6 &= 0 \\
1,2x – 0,6 &= 0 \,\,\, |+0,6 \\
1,2x &= 0,6 \,\,\, |:1,2 \\
x &= 0,5 \end{align}
Diese 0,5 kannst du nun in den Flächenterm aus 1.3 einsetzen und die Aufgabe schnell lösen.
\begin{align} A(0,5) &= -0,3 \cdot 0,5^2 + 1,5 \cdot 0,5 + 15,3 \\
\Rightarrow &A(0,5) = 15,98 FE \end{align}
