Lösung zu A1
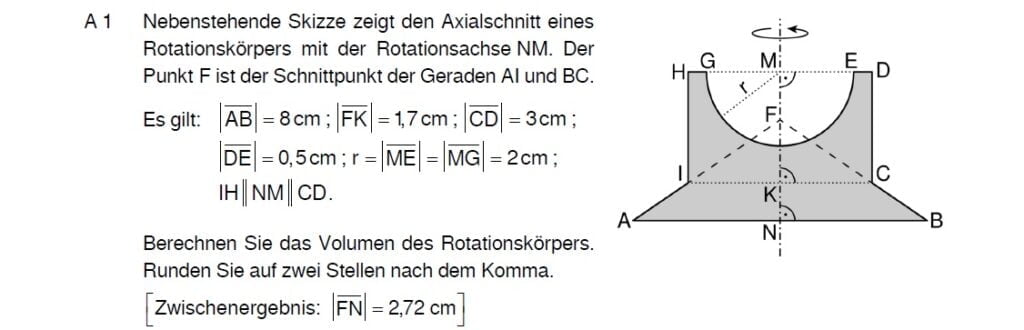
Der Körper setzt sich aus einem Kegelstumpf (ABCI) + einem Zylinder (CDHI) – die Halbkugel zusammen.
Der Kegelstumpf entsteht aus dem Kegel (ABF) – Kegel (CFI)
Der gesuchte Körper setzt sich aus einem Zylinder (CDHI), einer Halkugel (GE) und einem Kegelstumpf (ABCI) zusammen.
Den Kegelstumpf berechnest du, indem du vom großen Kegel (ABF) den kleinen Kegel (ICF) abziehst.
\begin{align} &\text{Berechnung benötigter Teilstrecken:}\\
\\
|\overline{IK}| &= |\overline{ME}| + |\overline{ED}| = 2 + 0,5 = 2,5 cm \\
|\overline{AN}| &= 0,5 \cdot |\overline{AB}| = 0,5 \cdot 8 = 4 cm \\
\\
&|\overline{FN}| \text{ über den Vierstreckensatz:}\\
\frac{|\overline{FN}|}{|\overline{FK}|} &= \frac{|\overline{AN}|}{|\overline{IK}|}\\
\frac{|\overline{FN}|}{1,7} &= \frac{4}{2,5} \,\,\, |\cdot 1,7 \\
|\overline{FN}|&= \frac{4}{2,5} \cdot 1,7 \\
\Rightarrow &|\overline{FN}| = 2,72 cm \\
\\
&\text{Berechnung der Teilvolumina:}\\
V_{Zylinder} &= \pi \cdot |\overline{IK}|^2 \cdot |\overline{IH}| \\
&= \pi \cdot 2,5^2 \cdot 3 \\
\Rightarrow &V_{Zylinder} = 58,90 cm^3 \\
\\
V_{Halbkugel} &= \frac{1}{2} \cdot \frac{4}{3} \cdot \pi \cdot |\overline{ME}|^3 \\
&= \frac{1}{2} \cdot \frac{4}{3} \cdot \pi \cdot 2^3 \\
\Rightarrow &V_{Halbkugel} = 16,76 cm^3 \\
\\
V_{Gr. Kegel} &= \frac{1}{3} \cdot \pi \cdot |\overline{AN}|^2 \cdot |\overline{FN}| \\
&= \frac{1}{3} \cdot \pi \cdot 4^2 \cdot 2,72 \\
\Rightarrow &V_{Gr. Kegel} = 45,57 cm^3 \\
\\
V_{kl. Kegel} &= \frac{1}{3} \cdot \pi \cdot |\overline{IK}|^2 \cdot |\overline{FK}| \\
&= \frac{1}{3} \cdot \pi \cdot 2,5^2 \cdot 1,7 \\
\Rightarrow &V_{kl. Kegel} = 11,13 cm^3 \\
\\
&\text{Zusammensetzen zum Gesamtvolumen:}\\
V &= V_{Zylinder} – V_{Halbkugel} + V_{gr. Kegel} – V_{kl. Kegel} \\
&= 58,90 – 16,76 + 45,57 – 11,13 \\
\Rightarrow V = 76,58 cm^3 \end{align}
