

Lösungen zu 2.1
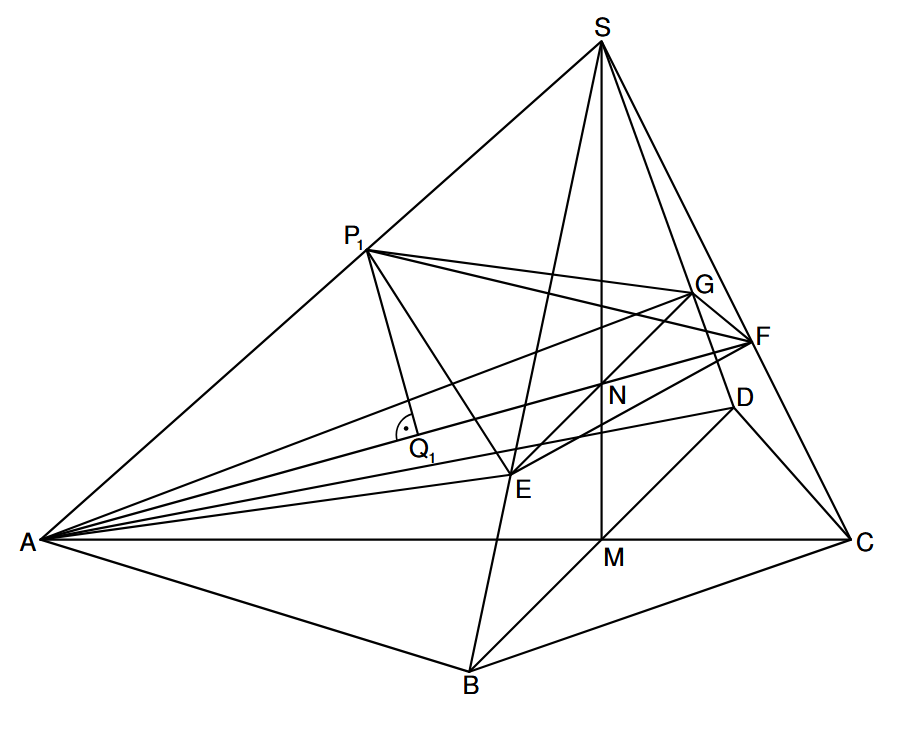
Für das Schrägbild muss du von M nach vorne und nach hinten. Achte darauf, dass die Strecke BD in der Zeichnung insgesamt 6 cm lang ist.
Weil die Höhe immer senkrecht steht, darfst du mit Sinus, Cosinus, Tangens und Satz des Pythagoras arbeiten.
\begin{align} &|\overline{AS}| \text{ mit dem Satz des Pythagoras:}\\
|\overline{AS}|^2 &= |\overline{AM}|^2 + |\overline{MS}|^2 \\
&= 9^2 + 8^2 \,\,\,|\sqrt{} \\
\Rightarrow &|\overline{AS}| = 12,04 \text{cm}\\
\\
&\angle SCA \text{ mit dem Tangens:}\\
tan(\angle SCA) &= \frac{|\overline{MS}|}{|\overline{AC}| – |\overline{AM}|} \\
&= \frac{8}{13-9} \,\,\, |tan^{-1}\\
\Rightarrow &\angle SCA = 63,43° \end{align}
Zurück zum MAP-Hack:

Lösungen zu 2.2
Eine Halbgerade fängt in einem Punkt an und geht über den anderen hinaus. Achte darauf in der Zeichnung.
Einzeichnen des Punktes N und der Strecke [AF]. – Siehe B2.1
\begin{align} &\angle CAF \text{ mit dem Tangens:}\\
tan(\angle CAF) &= \frac{|\overline{MN}|}{|\overline{AM}|} \\
&= \frac{2,5}{9} \\
\Rightarrow &\angle CAF = 15,52° \end{align}
Zurück zum MAP-Hack:

Lösungen zu 2.3
Den Flächeninhalt eines Drachenvierecks berechnest du am besten über die Flächenformel (\( A = e \cdot f \)), wobei die Diagonalen hier \( |\overline{AF}| \) und \( |\overline{EG}| \) heißen. Diese musst du zuerst berechnen, um einsetzen zu können.
Einzeichnen der Strecke \(\overline{EG}\) und das Drachenviereck AEFG. – Siehe B2.1
\begin{align} &|\overline{AF}| \text{ mit dem Sinussatz:}\\
\frac{|\overline{AF}|}{sin(\angle SCA)} &= \frac{|\overline{AC}|}{sin(\angle AFC)}\\
\text{mit } \angle AFC &= 180° – \angle SCA – \angle CAF \\
&= 180° – 63,43° – 15,52° \\
\frac{|\overline{AF}|}{sin(63,43°)} &= \frac{13}{sin(101,05°)} \,\,\, |\cdot sin(63,43°) \\
\Rightarrow &|\overline{AF}| = \frac{13}{sin(101,05°)} \cdot sin(63,43°) \\
&= 11,87 \text{cm} \\
\\
&|\overline{EG}| \text{ mit dem Vierstreckensatz:}\\
\frac{|\overline{EG}|}{|\overline{BD}|} &= \frac{|\overline{MS}|- |\overline{MN}|}{|\overline{MS}|}\\
\frac{|\overline{EG}|}{12} &= \frac{8 – 2,5}{8} \,\,\, |\cdot 12 \\
\Rightarrow &|\overline{EG}| = \frac{5,5}{8} \cdot 12 = 8,25 \text{cm} \\
\\
&\text{ Einsetzen in die Flächenformel}\\
A_{AEFG} &= 0,5 \cdot |\overline{AF}| \cdot |\overline{EG}| \\
&= 0,5 \cdot 11,87 \cdot 8,25 \\
\Rightarrow &A_{AEFG} = 48,96 \text{cm}^2 \end{align}
Das Ergebnis weicht aufgrund eines anderen Rechenweges vom Ersatzergebnis ab.
Leider habe ich im Video den Taschenrechner falsch abgeschrieben. Der Rechenweg passt, das Ergebni sist aber 48,88 nicht ,44. Bitte nicht wundern.
Zurück zum MAP-Hack:

Lösungen zu 2.4
Lies zuerst, für welchen Wert für x du einzeichnen musst!
Die Höhe steht immer senkrecht, du darfst also Sinus, Cosinus, Tangens und Satz des Pythagoras verwenden. Hier dann einfach in Abhängigkeit von x.
\begin{align} &\angle CAS \text{ mit dem Tangens:}\\
tan(\angle CAS) &= \frac{|\overline{MS}|}{|\overline{AM}|} \\
&= \frac{8}{9} \,\,\, |tan^{-1}\\
\Rightarrow &\angle CAS = 41,63° \\
\\
&\angle Q_n A P_n \text{ über Subtraktion:}\\
\angle Q_n A P_n &= \angle CAS – \angle CAF \\
&= 41,63° – 15,52° \\
\Rightarrow &\angle Q_n A P_n = 26,11° \\
\\
&\overline{P_n Q_n} \text{ mit dem Sinus:}\\
sin(\angle Q_n A P_n) &= \frac{|\overline{P_n Q_n}|}{x} \\
sin(26,11°) &= \frac{|\overline{P_n Q_n}|}{x}\,\,\, |\cdot x \\
\Rightarrow &|\overline{P_n Q_n}| = 0,44 \cdot x \text{ cm}\end{align}
Zurück zum MAP-Hack:

Lösungen zu 2.5
Zuerst stellst du die funktionale Volumenformel \( V(x) \) auf und setzt diese dann mit 14 gleich.
Die erhaltene Gleichung löst du nach x auf.
\begin{align} &V(x) \text{ mit der Pyramidenformel:}\\
V(x) &= \frac{1}{3} \cdot A_{AEFG} \cdot |\overline{P_n Q_n}| \\
&= \frac{1}{3} \cdot 48,88 \cdot 0,44 \cdot x \\
\Rightarrow &V(x) = 7,17 \cdot x \text{cm}^3\\
\\
&\text{ Gleichsetzen mit } 14: \\
7,17 \cdot x &= 14 \,\,\, |:7,17 \\
\Rightarrow &x = 1,95 \end{align}
Zurück zum MAP-Hack:
Das Vorgehen kommt „Arbeiten mit quadratischen Gleichungen“ aus den quadratischen Funktionen am nächsten.
