
Lösungen zu 1.1
Zwei Streckenlängen, aber kein Winkel mehr übrig? Verwende deinen Zirkel.
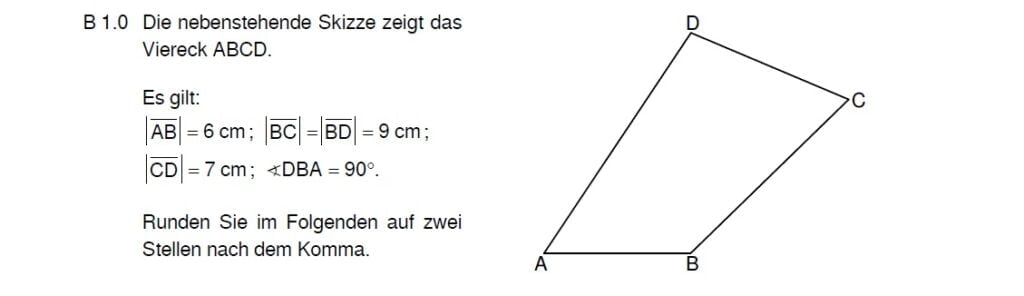
Der Umfang \( u \) ist die Summe aller begrenzenden Seiten. Hier kennst du alle, außer \( |\overline{DA}| \).
\begin{align}&|\overline{DA}| \text{ mit dem Satz des Pythagoras:}\\
|\overline{DA}|^2 &= |\overline{BD}|^2 + |\overline{AB}|^2 \\
&= 9^2 + 6^2 \,\,\, |\sqrt{}\\
\Rightarrow &|\overline{DA}| = 10,82 \text{cm}\\
\\
&\text{Berechnung des Umfangs durch Addition:}\\
u &= |\overline{AB}|+ |\overline{BC}|+ |\overline{CD}|+|\overline{DA}|\\
&= 6+ 9 +7 +10,82 \\
\Rightarrow &u = 32,82 \text{cm} \end{align}
Zurück zum MAP-Hack:
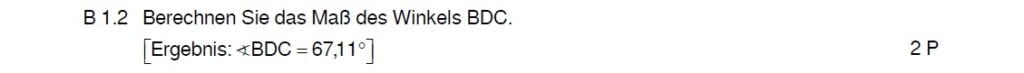
Lösungen zu 1.2
Drei Seiten sind gegeben, aber du hast keinen rechten Winkel. Sinussatz oder Cosinussatz?
\begin{align} &\angle BDC \text{ mit dem umgeformten Cosinussatz:}\\
cos(\angle BDC) &= \frac{|\overline{BD}|^2 + |\overline{CD}|^2 – |\overline{BC}|^2}{2 \cdot |\overline{BD}| \cdot |\overline{CD}|}\\
&= \frac{9^2 + 7^2 – 9^2}{2 \cdot 9 \cdot 7} \,\,\, |cos^{-1}\\
\Rightarrow &\angle BDC = 67,11° \end{align}
Zurück zum MAP-Hack:

Lösungen zu 1.3
Es gibt eine senkrechte Strecke, also darfst du mit Sinus, Cosinus, Tangens und dem Satz des Pythagoras arbeiten.
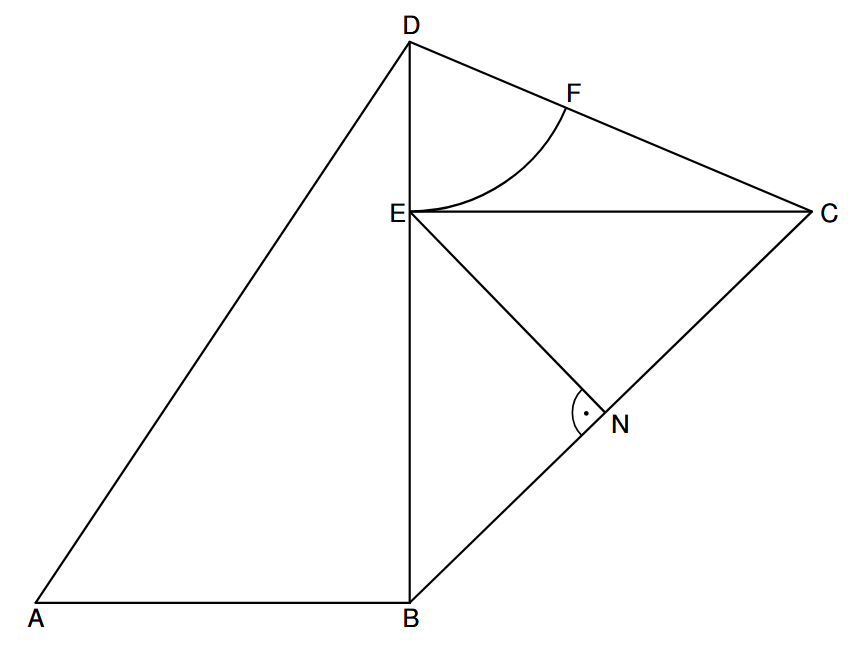
Einzeichnen der Strecke \(\overline{CE}\) – Siehe B1.1
\begin{align} &|\overline{CE}| \text{ mit dem Sinus:}\\
sin(\angle BDC) &= \frac{|\overline{CE}|}{|\overline{CD}|}\\
sin(67,11°) &= \frac{|\overline{CE}|}{7} \,\,\, |\cdot 7 \\
\Rightarrow &|\overline{CE}| = sin(67,11°) \cdot 7 = 6,45 \text{cm}\\
\\
&|\overline{DE}| \text{ mit dem Satz des Pythagoras:}\\
|\overline{CD}|^2 &= |\overline{DE}|^2 + |\overline{CE}|^2 \,\,\, \text{umstellen nach Kathete} \\
\Rightarrow |\overline{DE}|^2 &= |\overline{CD}|^2 – |\overline{CE}|^2 \\
&= 7^2 – 6,45^2 \,\,\, |\sqrt{}\\
\Rightarrow &|\overline{DE}| = 2,72 \text{cm} \end{align}
Zurück zum MAP-Hack:

Lösungen zu 1.4
Der Ansatz um die Aufgabe zu lösen ist, mit dem Sinus die Länge der Strecke [EN] zu bestimmen. Das funktioniert, weil die kürzeste Strecke die Eigenschaften des Abstandes hat, also im rechten Winkel steht.
Keine Ahnung was hier gemeint ist? Lies es hier Grundwissen nach: https://map-hack.de/grundwissen/eigenschaften-des-abstandes
Einzeichnen der Strecke \( \overline{EN}\) – Siehe B1.1
Um mit dem Sinus rechnen zu können, benötigst du den Winkel \( \angle CBD \).
Um an diesen Winkel zu kommen, benötigt es einen Trick. Das Dreieck ist gleichschenklig (\( |\overline{BD}| = |\overline{BC}| \)), also müssen auch die beiden Winkel an den Schenkeln gleich sein – beide jeweils 67,11°.
Den Winkel an der Spitze kannst du dann über die Innenwinkelsumme im Dreieck bestimmen. Genug geredet, jetzt wird gerechnet!
\begin{align} &\angle CBD \text{ über die Innenwinkelsumme im Dreieck:}\\
|\overline{BD}| &= |\overline{BC}|\, \Rightarrow \, \text{ Zwei Winkel} = 67,11° \\
\Rightarrow &\angle CBD = 180° – 2 \cdot 67,11° = 45,78° \\
\\
|\overline{BE}| &= |\overline{BD}| – |\overline{DE}| \\
&= 9 – 2,72 \\
\Rightarrow &|\overline{BE}| = 6,28 \text{cm}\\
\\
&|\overline{EN}| \text{ mit dem Sinus:}\\
sin(\angle CBD) &= \frac{|\overline{EN}|}{|\overline{BE}|} \\
sin(45,78°) &= \frac{|\overline{EN}|}{6,28}\,\,\, |\cdot 6,28 \\
\Rightarrow &|\overline{EN}| = sin(45,78°) \cdot 6,28 = 4,50 \text{cm}\end{align}
Zurück zum wichtigen Grundwissen:

Lösungen zu 1.5
Für gesuchte Fläche \( A_{BCFE} \) musst du von der Dreiecksfläche \( A_{BCD} \) die Kreissektorfläche \( A_{Sektor} \) abziehen.
Einzeichnen des Kreisbogens EF – Siehe B1.1
\begin{align} &A_{BCD} \text{ mit der Flächenformel:}\\
A_{BCD} &= \frac{1}{2} \cdot |\overline{BD}| \cdot |\overline{CD}|\cdot sin(\angle BDC) \\
&= \frac{1}{2} \cdot 9 \cdot 7 \cdot sin(67,11°) \\
\Rightarrow &A_{BCD}= 29,02 \text{cm}^2 \\
\\
&A_{Sektor} \text{ mit der Flächenformel:}\\
A_{Sektor} &= \frac{\angle BDC}{360°} \cdot |\overline{DE}| \cdot \pi \\
&= \frac{67,11°}{360°} \cdot 2,72^2 \cdot \pi \\
\Rightarrow &A_{Sektor} = 4,33 \text{cm}^2\\
\\
A_{BCFE} &= A_{BCD} – A_{Sektor} \\
&= 29,02 – 4,33 \\
\Rightarrow &A_{BCFE} = 24,69 \text{cm}^2 \end{align}

Ich habe eine Frage: Bei Aufgabe 1.4, bei der man EN berechnen muss, habe ich nur 1 Rechnung mit dem Kosinus stehen, weil man doch weiß, dass der Winkel BEN die Hälfte von BEC ist, da er in der Mitte geteilt wurde. Ich habe dann nur cos(45)=EN ÷ 6,28 stehen, geht das auch?
Prinziell gilt: Du darfst nicht davon ausgehen, dass irgendetwas so ist, nur weil es so aussieht. Dass der Winkel halbiert wird, müsste das Dreieck BCE gleichschenklig sein. Aber du weißt nicht, ob EC und EB gleichlang ist. Daher darfst du das leider nicht machen.
Die Ap 2023 NT B3 hat zweimal die Aufgabe B3.4 und keine B3.5
Danke für den Hinweis, ich habe den Namen im Lösungstab ausgetauscht