
Lösungen zu 3.1
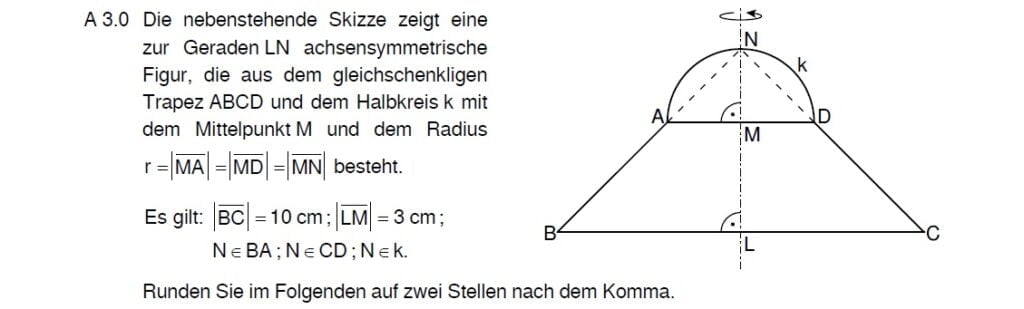
90° Winkel und ein Kreis, dafür gibt es einen Fachbegriff aus dem Grundwissen. Du musst ihn nur nennen.
Der Punkt N liegt auf dem Thaleskreis über \(\overline[AD}\), also gilt \( \angle AND = 90° \)
\begin{align} r \text{ mit dem Tangens:}\\
tan(0,5 \cdot \angle AND) &= \frac{0,5 \cdot |\overline{BC}|}{r + |\overline{LM}|}\\
tan(45°) &= \frac{5}{r+3} \,\,\, |\cdot (r+3) :tan(45°) \\
r + 3 &= \frac{5}{tan(45°)} \,\,\, | – 3 \\
\Rightarrow &r = 2 \text{cm}\end{align}
Zurück zum MAP-Hack:

Lösungen zu 3.2
Das gesuchte Volumen \( V\) setzt sich aus dem Kegelstumpf und der Halbkugel zusammen. Für das Volumen des Kegelstumpfes benötigst du das Volumen des großen Kegels \( V_K \) und des kleinen Kegels \( V_k \).
Berechne die drei Teilvolumina oder setzte alles in eine große Formel ein.
\begin{align} &V_K \text{ mit der Kegel-Formel:}\\
V_K &= \frac{1}{3} \cdot |\overline{BL}|^2 \cdot \pi \cdot |\overline{LN}| \\
&= \frac{1}{3} \cdot 5^2 \cdot \pi \cdot 5 \\
\Rightarrow &V_K = 130,90 \text{cm}^3 \\
\\
&V_k \text{ mit der Kegel-Formel:} \\
V_k &= \frac{1}{3} \cdot |\overline{AM}|^2 \cdot \pi \cdot |\overline{MN}| \\
&= \frac{1}{3} \cdot 2^2 \cdot \pi \cdot 2\\
\Rightarrow &V_k = 8,38 \text{cm}^3 \\
\\
&V_{HK} \text{ mit der Kugel-Formel:}\\
V_{HK} &= \frac{1}{2} \cdot \frac{4}{3} \cdot |\overline{AM}|^3 \cdot \pi \\
&= \frac{1}{2} \cdot \frac{4}{3} \cdot 2^3 \cdot \pi \\
\Rightarrow &V_{HK} = 16,76 \text{cm}^3 \\
\\
\Rightarrow &V = V_{HK} + V_K – V_k = 139,28 \text{cm}^3 \end{align}
