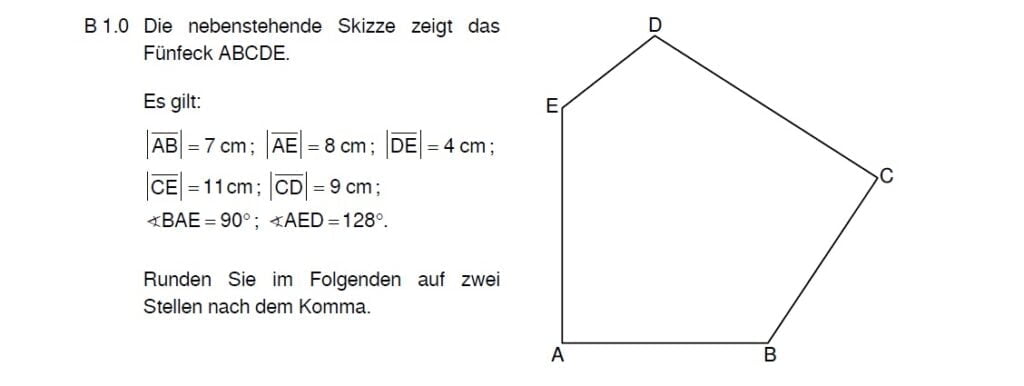

Lösungen zu 1.1
Beim Zeichnen zwei Strecken, aber keinen Winkel übrig? Benutze deinen Zirkel.
Für die Berechnungen suchst ud dir ein rechtwinkliges Dreieck und benutzt einen passenden Ansatz.
\begin{align} &|\overline{BE}|\text{ mit dem Satz des Pythagoras:}\\
|\overline{BE}|^2 &= |\overline{AB}|^2 + |\overline{AE}|^2 \\
&= 7^2 + 8^2 \,\,\, |\sqrt{} \\
&\Rightarrow |\overline{BE}| = 10,63 cm \\
\\
&\angle AEB \text{ mit dem Tangens:}\\
tan(\angle AEB) &= \frac{|\overline{AB}|}{|\overline{AE}|} \\
&= \frac{7}{8} \,\,\, |tan^{-1}\\
&\Rightarrow \angle AEB = 41,19°\end{align}
Zurück zum MAP-Hack:

Lösungen zu 1.2
Zerlege das Viereck in zwei Dreiecke und berechne deren Flächenninhalte.
\begin{align} &\text{ Berechnugn des Flächeninhalts von ABE:}\\
A_{ABE} &= \frac{1}{2} \cdot |\overline{AB}| \cdot |\overline{AE}| \\
&= \frac{1}{2} \cdot 7 \cdot 8 \\
&\Rightarrow A_{ABE} = 28 cm^2 \\
\\
&\angle BEC \text{ über } \angle CED \text{ mit dem umgestellten Coisnussatz:}\\
cos(\angle CED) &= \frac{|\overline{ED}|^2 + |\overline{EC}|^2 – |\overline{CD}|^2}{2 \cdot |\overline{EC}| \cdot |\overline{ED}|} \\
&= \frac{4^2 + 11^2 – 9^2}{2 \cdot 11 \cdot 4} \,\,\, |cos^{-1} \\
&\Rightarrow \angle CED = 50,48° \\
\\
\angle BEC &= 128° – 41,19° – 50,48° = 36,33° \\
\\
&\text{ Berechnung des Flächeninhalts von BCE:}\\
A_{BCE} &= \frac{1}{2} \cdot |\overline{EB}| \cdot |\overline{EC}| \cdot sin(\angle BEC)\\
&= \frac{1}{2} \cdot 10,63 \cdot 11 \cdot sin(36,33°)\\
&\Rightarrow A_{BCE} = 34,64 cm^2 \\
\\
&\text{Berechnung des gesuchten Flächeninhalts:}\\
A_{ABCE} &= A_{ABE} + A_{BCE} \\
&= 28 + 34,64 \\
&\Rightarrow A_{ABCE}= 62,64 cm^2 \end{align}
Zurück zum MAP-Hack:
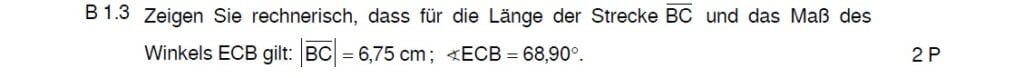
Lösungen zu 1.3
Dreieck mir 3 Angaben suchen, ausrechnen. Achte darauf, ob das Dreieck rechtwinklig ist.
\begin{align} &|\overline{BC}| \text{ mit dem Cosinussatz:}\\
|\overline{BC}|^2 &= |\overline{EB}|^2 + |\overline{EC}|^2 – 2 \cdot |\overline{EB}| \cdot |\overline{EC}| \cdot cos(\angle BEC) \\
&= 10,63^2 + 11^2 – 2 \cdot 10,63 \cdot 11 \cdot cos(36,33°) \,\,\, |\sqrt{} \\
&\Rightarrow \overline{BC} = 6,75 cm \\
\\
&\angle ECB \text{ mit dem umgeformten Cosinussatz:}\\
cos(\angle ECB) &= \frac{ |\overline{EC}|^2 + |\overline{BC}|^2 – |\overline{EB}|^2}{2 \cdot |\overline{EC}| \cdot |\overline{BC}|} \\
&= \frac{11^2 + 6,75^2 – 10,63^2}{2 \cdot 11 \cdot 6,75} \,\,\, |cos^{-1}\\
&\Rightarrow \angle ECB = 68,86° \end{align}
Das Ergebnis stimmt wegen Rundungsfehlern nicht mit dem Ersatzergebnis überein, stimmt aber trotzdem.
Zurück zum MAP-Hack:

Lösungen zu 1.4
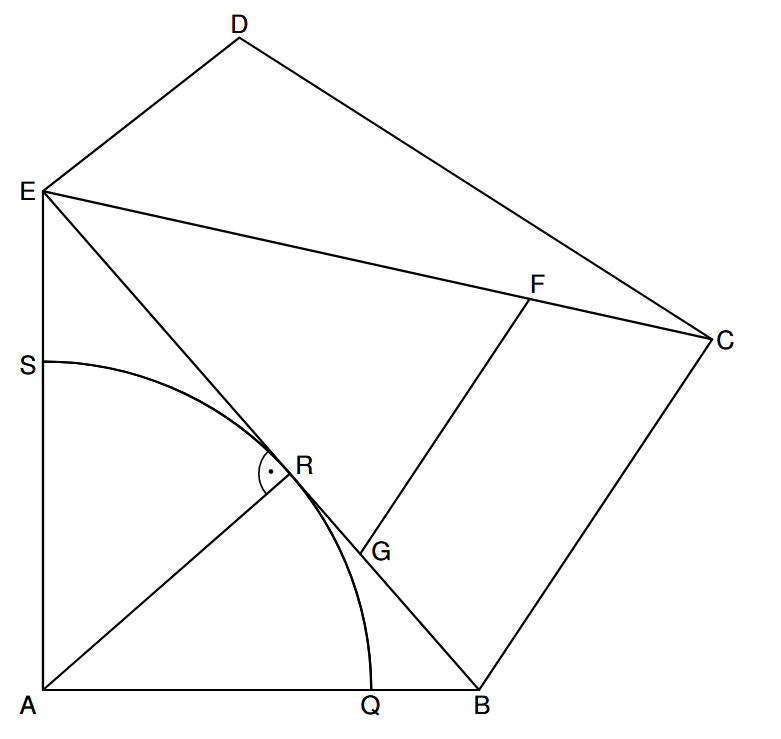
Du kannst den Flächeninhalt des Dreiecks CBE berechnen und dann das Dreieck EGF abziehen. Eine andere Möglichkeit ist, dass man die Höhe des Trapezes über den Winkel bei C bestimmt und dann mit der Trapez-Flächenformel arbeitet.
Die Zeichnung findest du in B1.1
In dieser Lösung wird der Flächeninhalt berechnet, indem man vom Dreieck CBE das Dreieck EGF abzieht. Eine andere Möglichkeit ist, dass man die Höhe des Trapezes über den Winkel bei C bestimmt und dann mit der Trapez-Flächenformel arbeitet.
\begin{align} &|\overline{EG}| \text{ mit dem Vierstreckensatz:}\\
\frac{|\overline{EG}|}{|\overline{EB}|} &= \frac{|\overline{EF}|}{|\overline{EC}|} \,\,\, |\cdot |\overline{EB}| \\
|\overline{EG}| &= \frac{8 \cdot 10,63}{11} \\
&\Rightarrow |\overline{EG}| = 7,73 cm \\
\\
&\text{ Berechnung des Flächeninhalts von EGF:}\\
A_{EGF} &= \frac{1}{2} \cdot |\overline{EF}| \cdot |\overline{EG}| \cdot sin(\angle BEC)\\
&= \frac{1}{2} \cdot 8 \cdot 7,73 \cdot sin(36,33°)\\
&\Rightarrow A_{EGF} = 18,32 cm^2 \\
\\
&\text{ Berechnung des Flächeninhalts von BCFG:}\\
A_{BCFG} &= A_{BCE} – A_{EGF} \\
&= 34,64 – 18,32 \\
&\Rightarrow A_{BCFG} = 16,32 cm^2 \end{align}
Zurück zum MAP-Hack:

Lösungen zu 1.5
Rechte Winkel machen das Rechnen leichter. Wo findest du einen für AR?
Die Zeichnung findest du in B1.1
\begin{align} &|\overline{AR}| \text{ mit dem Sinus:}\\
sin(\angle AER) &= \frac{|\overline{AR}|}{|\overline{AE}|} \,\,\, |\cdot |\overline{AE}| \\
\overline{AR} &= sin(41,19°) \cdot 8 \\
&\Rightarrow |\overline{AR}|= 5,27 cm \\
\\
&\text{ Berechnung des Flächeninhalts des Sektors:}\\
A &= \frac{\angle BAE}{360^°} \cdot |\overline{AR}|^2 \cdot \pi \\
&= \frac{90°}{360°} \cdot 5,27^2 \cdot \pi \\
&\Rightarrow A = 21,81 cm^2 \end{align}
