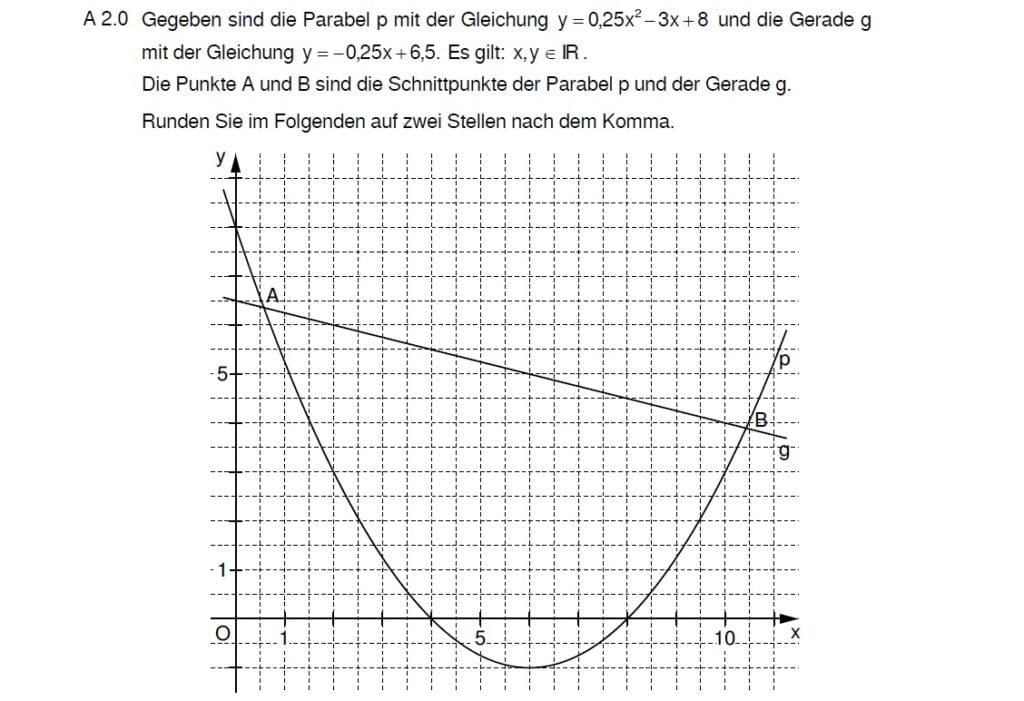
Lösungen zu 2.1
Es ist dasselbe Vorgehen, wie bei „Intervallgrenzen bestimmen“, nur dass du am Ende die x-Koordinaten in die Funktionsterme einsetzen musst, um die y-Koordinate der Schnittpunkte zu bestimmen.
\begin{align} &\text{Gleichsetzen der Funktionsterme:}\\
y_{Parabel} &= y_{Gerade}\\
0,25x^2-3x+8 &=-0,25x + 6,5 \,\,\, |+0,25x -6,5\\
0,25x^2 – 2,75x + 1,5 &= 0 \\
\Rightarrow >R \\
\Rightarrow x_B = 10,42 \,\,\,&\,\,\, x_A = 0,58\\
\\
&\text{Berechnung der Koordinaten über die Gerade:}\\
y_B &= -0,25 \cdot x_B + 6,5 \\
&= -0,25\cdot 10,42 + 6,5 \\
y_B &= 3,90 \\
&\Rightarrow B(10,42|3,90)\\
\\
y_A &= -0,25 \cdot x_A + 6,5 \\
y_A &= 6,36\\
&\Rightarrow A(0,58|6,36)\end{align}
Zurück zum MAP-Hack:
Lösungen zu 2.2
An welcher Stelle für x musst du einzeichnen? Gehe hier zu den Funktionsgraphen. Suche anschließend den Mittelpunkt.
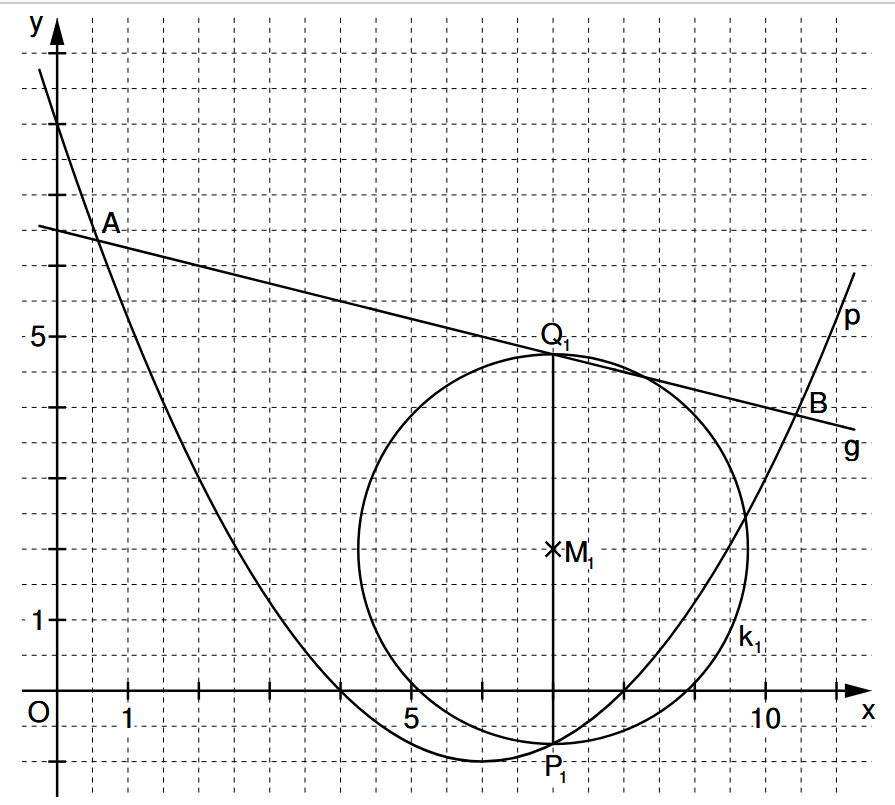
Zurück zum MAP-Hack:
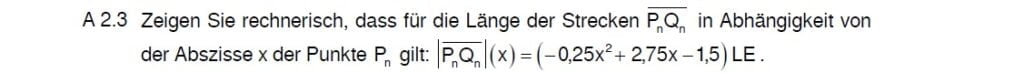
Lösungen zu 2.3
P und Q haben dieselbe Abszisse, setze mit „Oben – Unten“ an.
\begin{align} &|\overline{P_nQ_n}|\text{ über „Oben – Unten“}\\
|\overline{P_nQ_n}| &= y_{Gerade} – y_{Parabel} \\
&= – 0,25x + 6,5 – (0,25x^2 – 3x + 8) \\
&= – 0,25x + 6,5 – 0,25x^2 +3x – 8 \\
&|\Rightarrow \overline{P_nQ_n}| = (-0,25x^2 + 2,75x – 1,5) LE \end{align}
Zurück zum MAP-Hack:
Lösungen zu 2.4
Der Taschenrechner kann dir die längste Strecke von PQ ausrechnen. Damit bestimmt du den maximalen Umfang.
Der Umfang ist genau dann maximal, wenn der Radius bzw. der Durchmesser maximal wird. Mit der Länge der Strecke [PQ] kannst du die maximale Länge mit deinem Taschenrechenr bestimmen:
\begin{align} \text{Taschenrechner: } x &= 5,5 \text{ mit } \overline{P_0 Q_0} = d_{max} = 6,06 LE \\
&\Rightarrow r_{max} = 3,03 LE \\
u_{max} &= 2 \cdot \pi \ r_{max} = 2 \cdot \pi \cdot 3,03 = 19,04 LE \end{align}
Lösungen zu 2.5
Mach ein Zahlenbeispiel: Wenn k2 einen Durchmesser von 1 hat, wie groß ist dann sein Flächeninhalt?
Welchen Durchmesser hat k3 in diesem Fall? Wie groß ist der Flächeninhalt von k3? Was hat dieses Zahlenbeispiel mit der Aussage zu tun?
DON’T PANIC! Das hier ist die Lösung eines Mathe-Lehrers. Die Lösung kann man auf viele Arten aufschreiben, z.B. auch mit einem Beispiel.
\begin{align} &\text{Allgemeine Begründung an Termen:}\\
d_3 &= 4 \cdot d_2 \Rightarrow r_3 = 4 \cdot r_2\\
\\
A_2 &= r_2^2 \cdot \pi \\
A_3 &= r_3^2 \cdot \pi \\
&= (4 \cdot r_2)^2 \cdot \pi \\
&= 16 \cdot r_2^2 \cdot \pi \\
A_3 &= 16 \cdot A_2 \end{align}
Die Aussage stimmt.
Unser Lehrer kann überhaupt nicht erklären und uns fehlt in der 10 ten Klasse teils noch 9. Klasse Stoff. Dazu habe ich diskalkulie und komme deswegen noch schlechter zu recht. Ich habe sehr Angst vor dem Abschluss, der ja in ein paar Tagen ist.
Mach‘ dir keinen Stress. Du brauchst nicht alle Themen aus der 9. Klasse. Rechne einfach in den nächsten Tagen so viele Aufgaben wie möglich. In der AP kommen häufig ähnliche Aufgaben dran. Du schaffst das schon!