

Lösungen zu B1.1
Die Berechnung der Parabelgleichung in dieser Aufgabe ist einzigartig. Nur hier brauchst du dieses Vorgehen. Manche Dinge bleiben aber gleich: Es ist der Scheitelpunkt gegeben, also verwendest du die Scheitelform \( y = a \cdot (x – x_s)^2 + y_s \). Dort setzt du für \(x_s\) und \(y_s\) die Koordinaten des Scheitelpunkts ein. Wenn du jetzt für x und y die Koordinaten von P einsetzt, so erhälst du eine Gleichung, in der du nur a nicht kennst. Du kannst sie also nach a auflösen und diesen Wert bestimmen (a = -0,25). Diesen setzt du jetzt statt P in die Scheitelform ein, löst die Klammer mit einer binomischen Formel auf und vereinfachst soweit wie möglich.
\begin{align} &Einsetzen \, von \, S \, und \, P: \\
Scheitelform: \, y &= a \cdot (x – x_S)^2 + y_s \\
S(4|2)\, \in p \\
y &= a \cdot (x – 4)^2 + 2 \\
P(-2|-7) \in p: \\
-7 &= a \cdot (-2 -4)^2 + 2 \\
-7 &= a \cdot (-6)^2 + 2 \,\,\ |-2 \\
-9 &= 36a \,\,\ |:36 \\
\Rightarrow a &= -0,25 \\
&Einsetzen \, in die Scheitelform: \\
y = -0,25 \cdot (x – 4)^2 + 2 \\
&= -0,25 \cdot (x^2 – 8x + 16) + 2 \\
&= -0,25x^2 + 2x – 4 + 2 \\
\Rightarrow &y = -0,25x^2 + 2x – 2 \end{align}
Zurück zum MAP-Hack:

Lösung zu B1.2

Zurück zum MAP-Hack:
Lösung zu B1.3
Um in die Flächenformel des Trapezes (\( A_{Trapez} = 0,5 \cdot (a + c) \cdot h \) ) einsezten zu können, benötigst du die Länge der Strecke \( a = \overline{A_n B_n} \). Weil A und B die selbe Abszisse haben, kannst du diese Länge durch „Oben – Unten“ berechnen.
\begin{align} &\overline{A_n B_n} \text{ durch „oben – unten“:} \\
\overline{A_n B_n} &= y_{Gerade} – y_{Parabel} \\
&= -0,5x + 5 – (-0,25x^2 + 2x -2) \\
&= -0,5x + 5 + 0,25x^2 – 2x + 2 \\
\Rightarrow &\overline{A_n B_n} = 0,25x^2 -2,5x + 7 \\
\\
& \text{Einsetzen, in die Flächenformel:} \\
A &= 0,5 \cdot (\overline{A_n B_n} + \overline{C_n D_n}) \cdot h \\
&= 0,5 \cdot (0,25x^2 -2,5x + 7 +6) \cdot 4 \\
&= 2 \cdot ( 0,25x^2 -2,5x + 13) \\
\Rightarrow &A(x) = (0,5x^2 -5x +26) FE \end{align}
Zurück zum MAP-Hack:

Lösung zu B1.4
Berechne den Extremwert des Terms \( A(x) = 0,5x^2 -5x + 26 \) mit deinem Taschenrechner.
\( \Rightarrow A_{min} = 13,5 FE \, für \, x \, = \, 5 \)Zurück zum MAP-Hack:

Lösung zu B1.5
Zuerst berechnest du den Wert für x, für den das Trapez einen FE von 25 hat. Das machst du mit einer Gleichung:
\begin{align} &\text{Wert für x mit einer Gleichung:} \\
A(x) &= 25 \\
0,5x^2 -5x +26 &= 25 \, \, \, |-25 \\
0,5x^2 – 5x + 1 &= 0 \\
\Rightarrow >R: \, x = 0,20 \, \lor \, x = 9,80 \end{align}
Wenn die Trapeze gleichzeitig Rechtecke sind, dann ist die Höhe des Trapezes genauso lang, wie seine Seitelänge. Es ergibt sich also eine Grundseite von 6 LE und eine Höhe von 4 LE. Damit würde sich auch ein Flächeninhalt von \( 4 \cdot 6 = 24 FE \) ergeben. Das trifft hier aber nicht zu. Also sind die Trapeze auch keine Rechtecke.
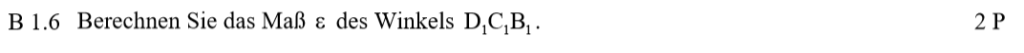
Lösung zu B1.6
Mit dem Tangens und der Höhe des Trapezes kannst du den Winkel bei C bestimmen. Hierzu musst du von der Grundseite CD die Parallele AB gegenüber abziehen. Wenn du diese Streckenlänge durch zwei teilst, erhältst du eine Seite der „Trapezflügel“.
Die Länge der Strecke AB kannst du bestimmen, indem du in den Term aus 1.3 einsetzt.

Von wo weis man das die strecke CD links liegen muss und nicht rechts?
Figuren werden immer gegen den Uhrzeigersinn beschriftet. So heißt das Trapez ABCD, wenn du ab nach links zeichnest und A oben ist, wären die Punkte in der Reihenfolge ABDC
Du hast eine Frage zu einer Teilaufgabe oder zur Lösung? Schreib‘ hier und du bekommst eine Antwort!