2019 Haupttermin Teil B1: Ebene Geometrie

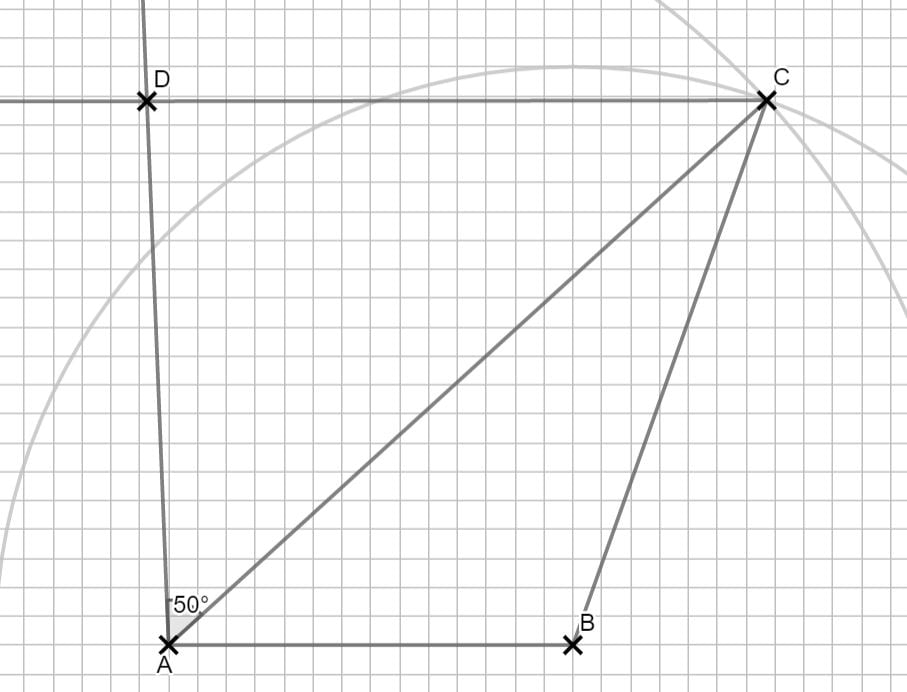
\begin{align}& \beta \, mit \, dem \, umgeformten \, Cosinussatz: \\ \overline{AC}^2 &= \overline{AB}^2 + \overline{BC}^2 – 2 \cdot \overline{AB} \cdot \overline{BC} \cdot cos(\beta) \\ cos(\beta) &= \frac{\overline{AB}^2 + \overline{BC}^2 – \overline{AC}^2}{2 \cdot \overline{AB} \cdot \overline{BC}} \\&= \frac{7^2 + 10^2 – 14^2}{2 \cdot 7 \cdot 10} \\ \Rightarrow &\beta = 109,62° \\ \\ & \varepsilon \, mit \, dem \, Sinussatz: \\ \frac{sin(\varepsilon)}{\overline{BC}} &= \frac{sin(\beta)}{\overline{AC}} \,\,\, |\cdot \overline{BC} \\ sin(\varepsilon) &= \frac{\overline{BC}}{\overline{AC}} \cdot sin(\beta) \\ &= \frac{10}{14} \cdot sin(109,62°) \\ \Rightarrow &\varepsilon = 42,28° \end{align}

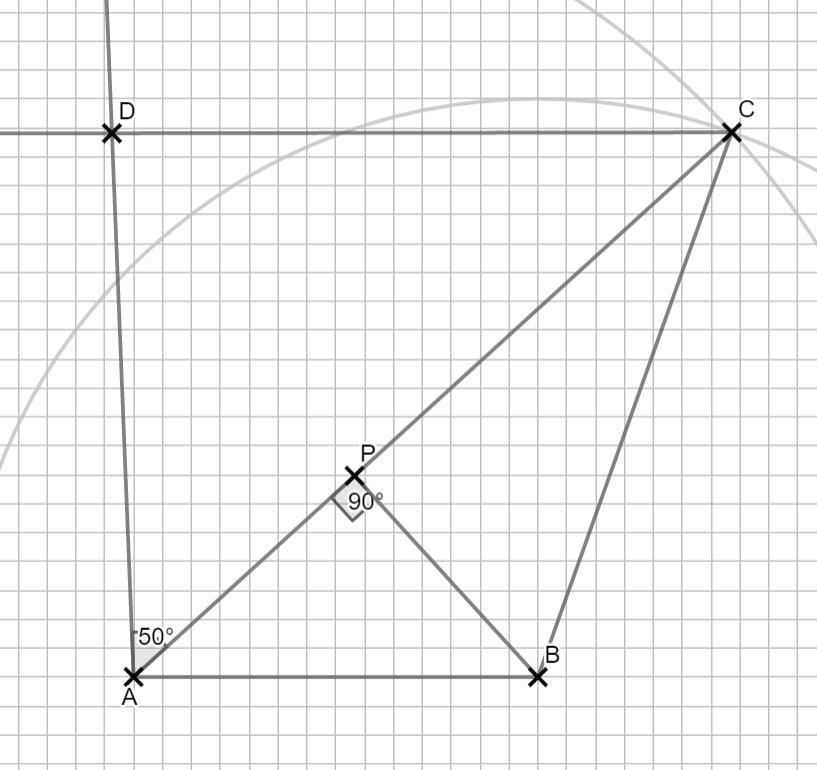
\begin{align} &\overline{BP} \, mit \, dem \, Sinus: \\ sin(\varepsilon) &= \frac{\overline{BP}}{\overline{AB}} \, \, \ |\cdot \overline{AB} \\ \overline{BP} &= \overline{AB} \cdot sin(\varepsilon) \\ &= 7 \cdot sin(42,28°) \\ \overline{BP} &= 4,71 cm \\ \\ &\overline{AP} \, mit \, dem \, Cosinus: \\ cos(\varepsilon) &= \frac{\overline{AP}}{\overline{AB}} \,\,\, |\cdot \overline{AB} \\ \overline{AP} &= cos(\varepsilon) \cdot \overline{AB} \\ &= cos(42,28°) \cdot 7 \\ \Rightarrow &\overline{AP} = 5,18 cm \\ \\ &Berechnung \, des \, Umfangs: \\ u &= \overline{AB} + \overline{BP} + \overline{AP} \\ &= 7 + 4,71 + 5,18 \\ \Rightarrow &u = 16,89 cm \end{align}

Um in die Flächenformel des Tapezes (\( A = 0,5 \cdot (a + c) \cdot h) \)) einsetzen zu können, benötigst du eine Höhe h und die Länge der Strecken [CD]. Die Länge von [AB] ist gegeben.

Achtung Falle: [DA] ist KEINE Höhe, da kein rechter Winkel zu [AB] vorliegt!

Um die Höhe zu berechnen, wirfst du ein Lot mit Lotfußpunkt D’ auf [DC] durch B. Diese Strecke sieht wie eine Parallele zu [AD] durch B ist… aber sie sieht nur so aus und ist nicht wirklich parallel.
Im Dreieck D’BC kannst du die Höhe bestimmen:

\begin{align} &\overline{D’B} \, mit \, dem \, Cosinus: \\
cos(\angle CBD’) &= \frac{\overline{D’B}}{\overline{BC}} \,\,\, |\cdot \overline{BC} \\
\overline{D’B} &= \overline{BC} \cdot cos(\angle CBD’) \\
&= 10 \cdot cos(109,62° – 90°) \\
\Rightarrow &\overline{D’B} = 9,42 cm \\
\\
&\angle ADC \, mit \, der \, Innenwinkelsumme: \\
180° &= \angle ADC + \angle DCA + \angle CAD \\ \angle ADC &= 180° – \angle DCA – \angle CAD \\ &= 180° – 42,28° – 50° \\ \Rightarrow &\angle ADC = 87,72° \\
\\ & \overline{CD} \, mit \, dem \, Sinussatz: \\
\frac{\overline{CD}}{sin(\angle CAD)} &= \frac{\overline{AC}}{sin(\angle ADC)} \,\,\, |\cdot sin(\angle CAD) \\ \overline{CD} &= \frac{ \overline{AC}}{sin(\angle ADC)} \cdot sin(\angle CAD) \\ &= \frac{14}{sin(87,72°)} \cdot sin(50°) \\ \Rightarrow &\overline{CD} = 10,73 cm \\ \\
&A_{Trapez}\, mit \, der \, Flächenformel: \\
A &= 0,5 \cdot ( \overline{AB} + \overline{CD} )\cdot \overline{D’B} \\ &= 0,5 \cdot (7 + 10,73) \cdot 9,42 \\ \Rightarrow &A_{Trapez} = 83,51 cm^2 \end{align}

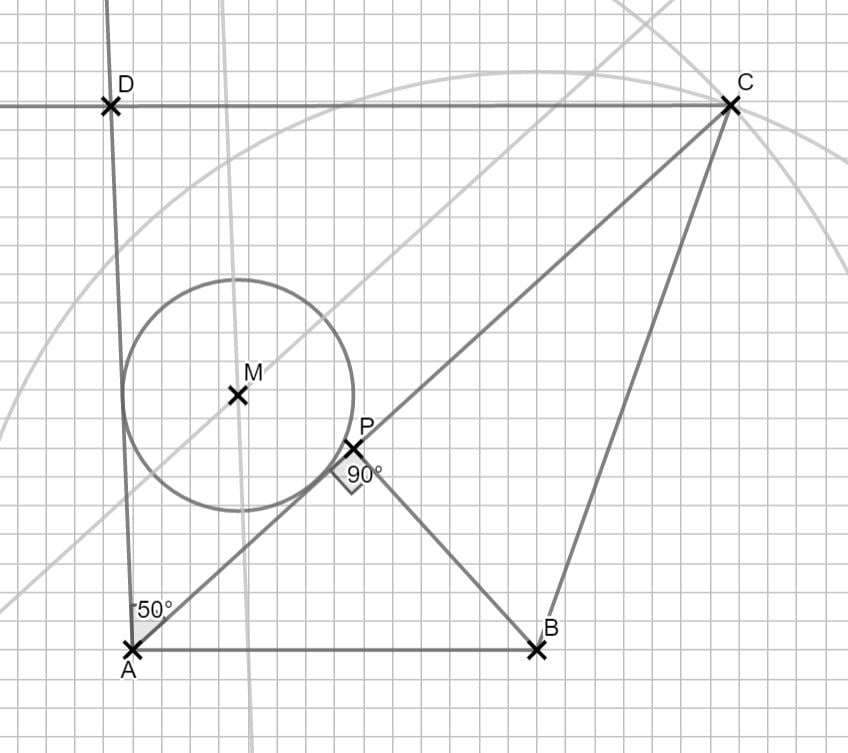
\begin{align} &A_{Kreis} \, mit \, der \, Flächenformel: \\ A_{Kreis} &= r^2 \cdot pi \\ &= 2^2 \cdot \pi \\ \Rightarrow &A_{Kreis}= 12,57 cm^2 \\ \\ &p \, mit \, der \, Prozentformel \\ p &= \frac{A_{Kreis}}{A_{Gesamt}} \cdot 100 \& \\ &= \frac{12,57}{83,51} \cdot 100 \% \\ \Rightarrow &p = 15,05 \% \end{align}

Die Figur setzt sich aus einem Drachenviereck AEMF und dem Kreisbogen zusammen. Das Drachenviereck besteht aus zwei rechtwinkligen Dreiecken. Damit ergbt sich als Zusammensetzung:

Um den Flächeninhalt des Dreiecks zu berechnen, benötigst du die Länge der Stecke [AE], für den Kreissektor den eingeschlossenen Winkel.

\begin{align} &\overline{AE} \, mit \, dem \, Tangens: \\ tan(\angle EAM) &= \frac{\overline{ME}}{\overline{AE}} \, \, \, |\cdot \overline{AE} : tan(\angle EAM) \\ \overline{AE} &= \frac{\overline{ME}}{tan(\angle EAM)} \\ &= \frac{2}{tan(25°)} \\ \Rightarrow &\overline{AE} = 4,29 \\ \\ &\angle FME \, mit \, der \, Innenwinkelsumme: \\ 360° &= \angle FME + \angle MEA + \angle EAF + \angle AFM \\ &= \angle 360° + 90° + 50° + 90° \\ \angle FME &= 360° – 90° – 50 ° – 90° \\ \Rightarrow &\angle FME = 130° \\ \\ & Berechnung des Flächeninhalts: \\ A &= 2 \cdot A_{Dreieck} – A_{Sektor} \\&= 2 \cdot 0,5 \cdot \overline{AE} \cdot \overline{ME} – \frac{\angle FME}{360°} \cdot \overline{ME}^2 \cdot \pi \\ &= 2 \cdot 0,5 \cdot 4,29 \cdot 2 – \frac{130°}{360°} \cdot 2^2 \cdot \pi \\ \Rightarrow &A = 4,04 cm^2 \end{align}