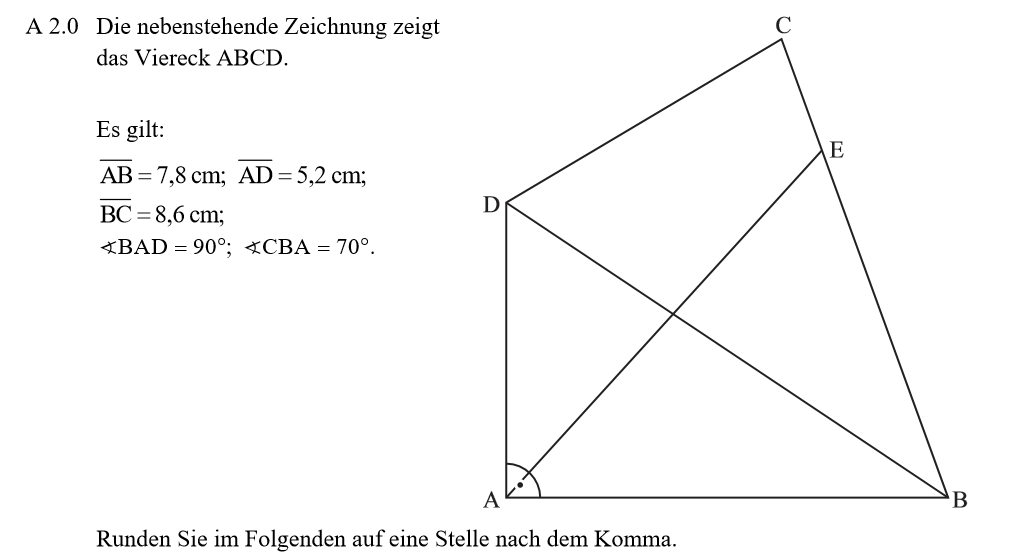
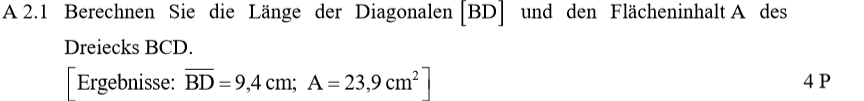
Lösung zu A2.1
Lösung als Text
Lösung als Video
\(\begin{align} &Berechung \, von \, \overline{BD} \\ \overline{BD}^2 &= \overline{AB}^2 + \overline{AD}^2 \\ \overline{BD} &= \sqrt{7,8^2 + 5,2^2} \\ \Rightarrow \overline{BD} &= 9,4 cm \\ \\ &Berechnung \, von \, \angle DBA: \\ tan(\angle DBA) & = \frac{\overline{AD}}{\overline{AB}} \\ tan(\angle DBA) &= \frac{5,2} {7,8} \\ \angle DBA &= 33,7° \\ \\ &Berechnung \, von \, \angle CDB: \\ \angle CBD &= \angle CBA – \angle DBA \\ \angle CBD &= 70° – 33,7° \\ \angle CBD &= 36,3° \\ \\ &Berechnung \, des \, Flächeninhalts: \\ A_{BCD} &= \frac{1}{2} \cdot \overline{BD}\cdot \overline{BC} \cdot sin(\angle CBD) \\ A_{BCD} &= \frac{1}{2} \cdot 9,4 \cdot 8,6 \cdot sin(36,3°) \\ A_{BCD} &= 23,9 cm^2 \end{align} \)
Zurück zum MAP-Hack:

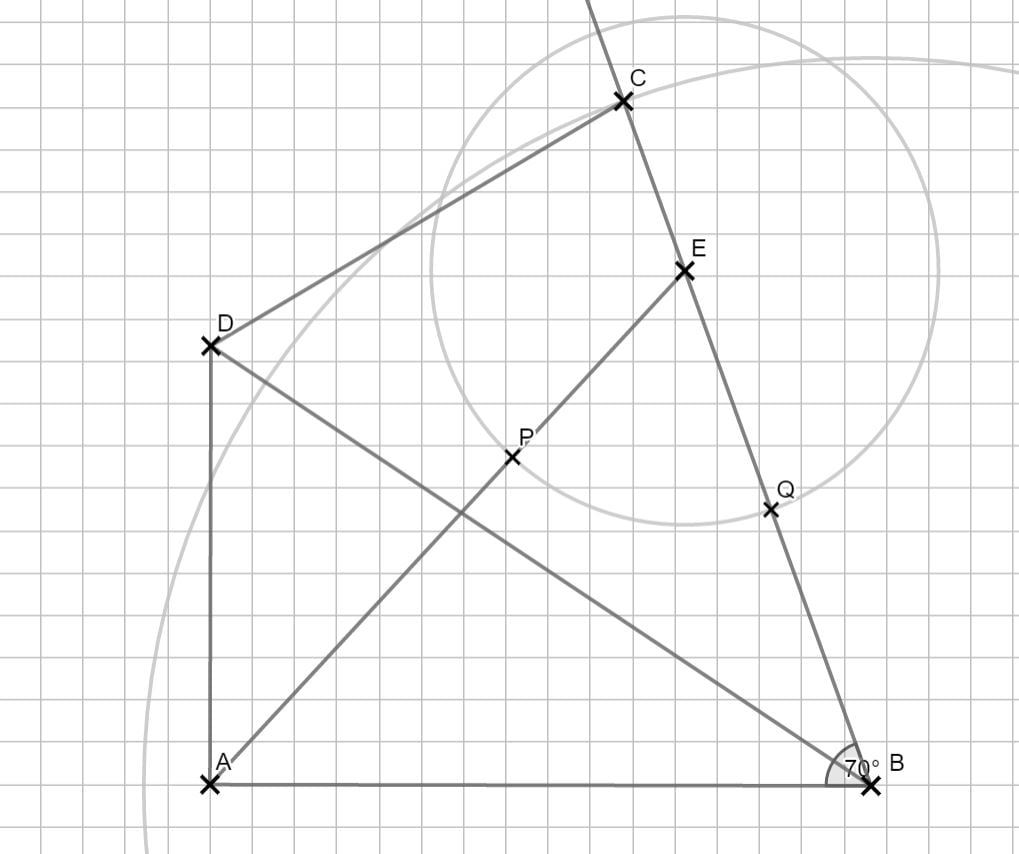
Lösung zu A2.2
Lösung als Text
Lösung als Video
Zuerst berechnest du \( \overline{BE} \) über den Flächeninhalt des Dreiecks, um dann mit dem Cosinussatz auf \( \overline{AE} \) zu schließen.
\( \begin{align} &Berechnung \,von \, \overline{BE}: \\A_{BCD} &= A_{ABE} \\
A_{BCD} &= \frac{1}{2} \cdot \overline{AB} \cdot \overline{BE} \cdot sin( \angle EBA) \,\,\, | \cdot \frac{2}{\overline{AB} \cdot sin(\angle EBA)} \\
\overline{BE} & = \frac{2 \cdot A_{BCD}}{\overline{AB} \cdot sin(\angle EBA)} \\
\overline{BE} &= \frac{2 \cdot 23,9}{7,8 \cdot sin(70°)} \\
\overline{BE} &= 6,5 cm \\
\\
&\overline{AE} \text{ mit dem Cosinussatz:}\\
\overline{AE} ^2 &= \overline{AB}^2 + \overline{BE}^2 – 2 \cdot \overline{AB} \cdot \overline{BE} \cdot cos(\angle DBA) \\
&= 7,8^2 + 6,5^2 -2 \cdot 7,8 \cdot 6,5 \cdot cos(70°) \,\,\, |\sqrt{}\\
&\Rightarrow \overline{AE} = 8,3 cm \end{align} \)
Zurück zum MAP-Hack:

Lösung zu A2.3
Lösung als Text
Lösung als Video

Du hast eine Frage zu einer Teilaufgabe oder zur Lösung? Schreib‘ hier und du bekommst eine Antwort!