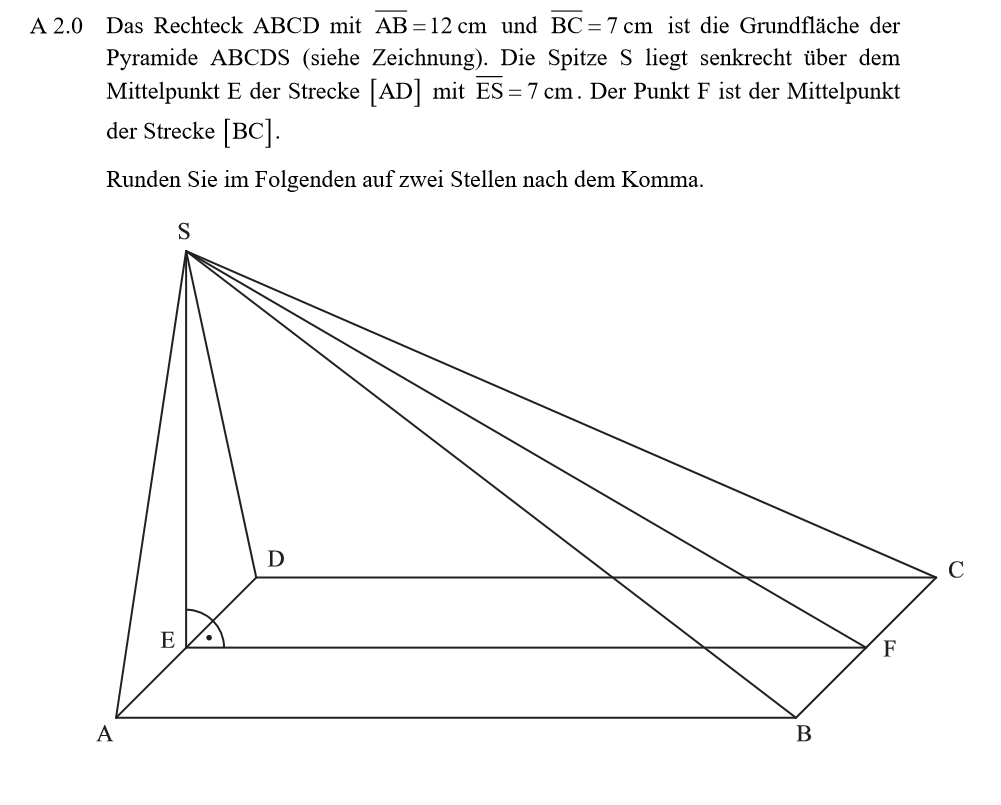
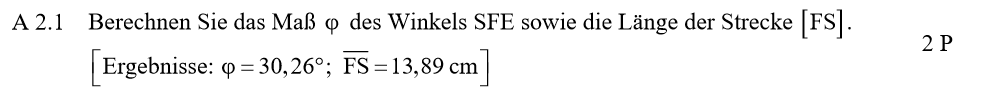
Lösung zu A2.1
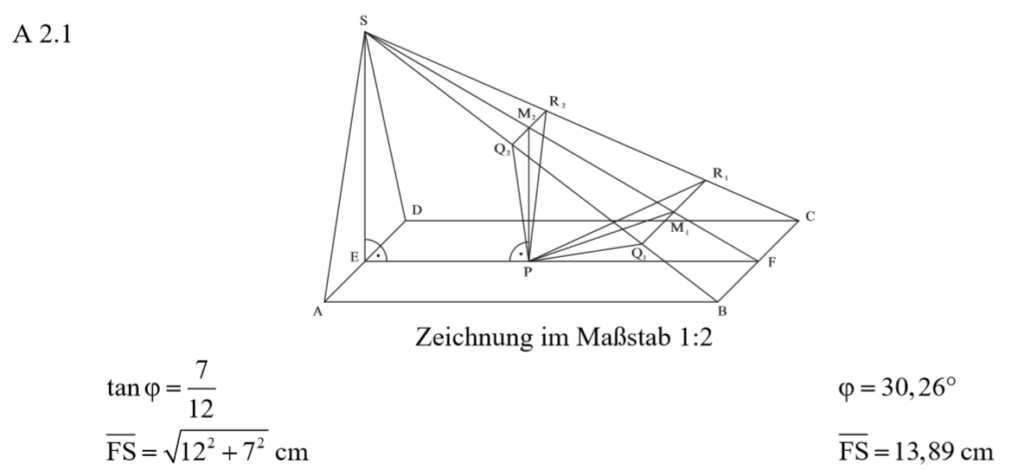
\begin{align} &\varphi \, mit \, dem \ Tangens: \\ tan( \varphi ) &= \frac{\overline{ES}}{\overline{EF}} \\ &= \frac{7}{12} \\ \Rightarrow &\varphi = 30,26° \\ \\ & \overline{FS} \, mit \, dem \, Satz \, des \, Pythagoras: \\ \overline{FS}^2 &= \overline{ES}^2 + \overline{EF}^2 \\ &= 7^2 + 12^2 \\ \Rightarrow &\overline{FS} = 13,89 cm. \end{align}
Zurück zum MAP-Hack:

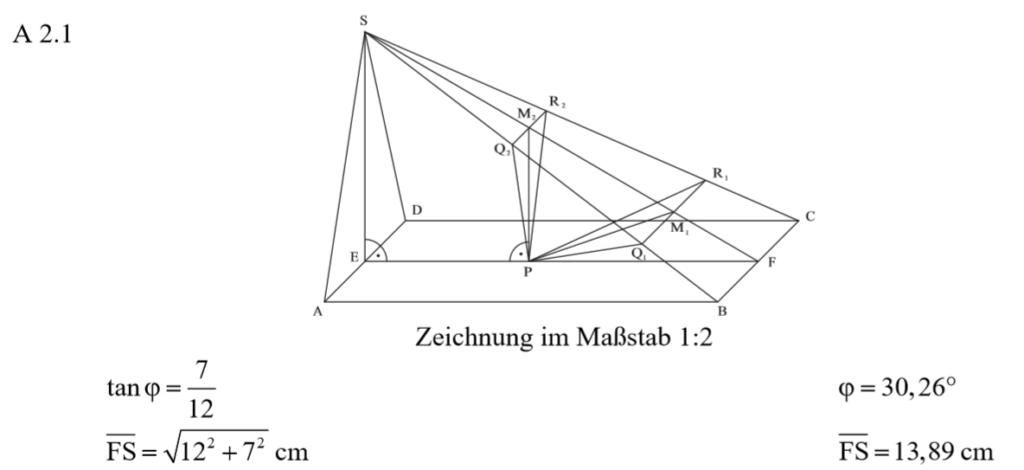
Lösung zu A2.2

Zurück zum MAP-Hack:

Lösung zu A2.3
\begin{align} & \overline{FM_2} \, mit \, dem \, Cosinus: \\ cos(\varphi) &= \frac{\overline{PF}}{\overline{FM_2}} \, \, \, |\cdot \overline{FM_2} : cos(\varphi) \\ \overline{FM_2} &= \frac{\overline{PF}}{cos(\varphi)} \\ &= \frac{12 – 5} {cos(30,26°)} \\ \Rightarrow &\overline{FM_2} = 8,10 \\ \Rightarrow &x=8,10 \\ \\ & \overline{R_2 M_2} \, mit \, dem \, Vierstreckensatz: \\ \frac{\overline{R_2 M_2}}{\overline{CF}} &= \frac{\overline{SM_2}}{\overline{FS}} \, \, \, |\cdot \overline{CF} \\ \overline{R_2 M_2} &= \frac{\overline{SM_2}}{\overline{FS}} \cdot \overline{CF} \\ mit &\overline{SM_2} = \overline{FS} – \overline{FM_2} \\ und \, & \overline{CF} = 0,5 \cdot \overline{BC} \\ \overline{R_2 M_2} &= \frac{13,89 – 8,1}{13,89} \cdot 3,5 \\ \Rightarrow &\overline{R_2 M_2} = 1,46 \\ \overline{R_2 Q_2} &= 2 \cdot \overline{R_2 M_2} \\ \Rightarrow &\overline{R_2 Q_2} = 2,92 cm \end{align}

Lösung zu A2.4
Um die Aufgabe lösen zu können, benötigst du das Volumen der Pyramide \( PR_2Q_2F \) und das Volumen der Pyramiade ABCDS. Anschließend kannst du den prozentualen Anteil bestiemmen. Für \( PR_2Q_2F \) brauchst du die \( \overline{PM_2} \)
\begin{align} &\overline{PM_2} \text{ mit dem Satz des Pythagoras:}\\
\overline{FM_2}^2 &= \overline{PM_2}^2 + \overline{PF}^2 \,\,\, |-\overline{PF}^2 \\
\overline{PM_2}^2 &= \overline{F_2M}^2 – \overline{PF}^2 \\
\overline{PM_2}^2 &= 8,1^2 – 7^2 \\
\Rightarrow &\overline{PM_2} = 4,08 \text{cm} \\
\\
&V_{PR_2Q_2F} \text{ mit der Volumenformel:}\\
V_{PR_2Q_2F} &= \frac{1}{3} \cdot \frac{1}{2} \cdot \overline{R_2Q_2} \cdot \overline{PM_2} \cdot \overline{PF} \\
&= \frac{1}{3} \cdot \frac{1}{2} \cdot 2,92 \cdot 4,08 \cdot 7 \\
\Rightarrow &V_{PR_2Q_2F} = 13,90 \text{cm}^3\\
\\
&V_{ABCDS} \text{ mit der Volumenformel:}\\
V_{ABCDS} &= \frac{1}{3} \cdot \overline{AB} \cdot \overline{BC} \cdot \overline{ES}\\
&= \frac{1}{3} \cdot 12 \cdot 7 \cdot 7 \\
\Rightarrow &V_{ABCDS} = 196 \text{cm}^3 \\
\\
&p \text{ mit der Prozentformel:}\\
p &= \frac{V_{PR_2Q_2F}}{V_{ABCDS}} \cdot 100 \% \\
&= \frac{13,90}{196}\cdot 100\% \\
\Rightarrow p&= 7,09 \% \end{align}

Sehr geehrter Herr Cobanov,
Erstmal vielen Dank für die tolle Seite, sie hilft sehr dabei sich für die Abschlussprüfung vorzubereiten.
Ich wollte Ihnen nur mitteilen, dass wenn man bei A2.4 auf „Lösung“ klickt, nur das Erklärvideo eingeblendet wird und nicht die Lösung als Text.
Mit Freundlichen Grüßen
Hallo Fabian,
danke für dein Feedback. Ich habe es gleich ausgebessert. Jetzt sieht man Text und Video in den entsprechenden Tabs.
Natürlich freut es mich, dass die Seite hilft. Danke auch für die netten Worte. Empfehle den MAP-Hack gerne den nächstjährigen 10. Klässler:innen.
Viel Erfolg! Tb.Cb
Hallo ,
bei der 2.3 heißt es ja , dass man den X-Wert bestimmen soll. Können Sie mir eventuell ganz allgemein erklären was man unter “X-Wert bestimmen” verstehen soll.
Danke im Voraus
Hallo Salma,
na klar kann ich das machen! das x legt den variablen Punkt Mn fest. Also je nachdem was das x ist, liegt auch der Punkt M woanders. Und hier ist eine Eigenschaft für M gegeben und du sollst den passenden Wert für x bestimmen, der diese Position festlegt.
Einfach mal probieren und sonst nochmal fragen =)
Tobias Cobanov