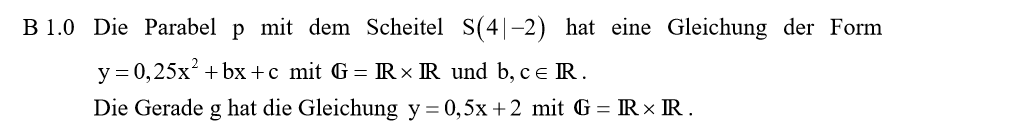
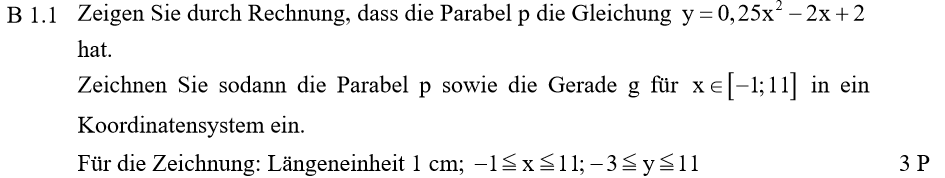
Lösung zu B1.1
Der Scheitelpunkt der Parabel ist gegeben, also arbeitest du mit der Scheitelform. Setze den Öffnungsfaktor 0,25, den du aus der Angabe weißt, in die Scheitelform \( y = a \cdot (x – x_s)^2 + y_s \) ein. Danach setzt du die Koordinaten von S(4|-2) ein. Löse die Klammer mit einer binomischen Formel auf und vereinfache soweit wie möglich.
\begin{align} y &= a \cdot (x – x_s)^2 + y_s \, \text{mit S(4|-2)}\\
&= 0,25 \cdot (x – 4 )^2 – 2 \\
&= 0,25 \cdot (x^2 – 8x + 16) – 2 \\
&= 0,25x^2 – 2x + 4 – 2 \\
\Rightarrow &y = 0,25x^2 – 2x + 2 \end{align}
Zurück zum MAP-Hack:

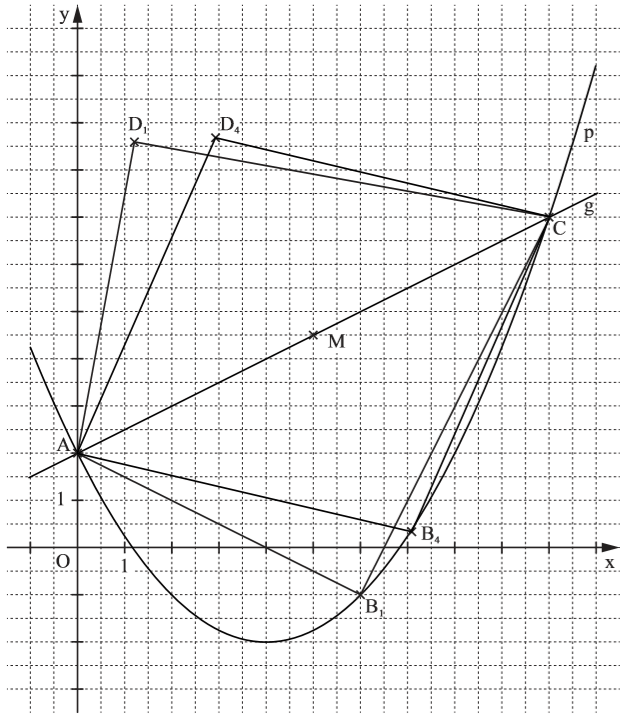
Lösung zu B1.2
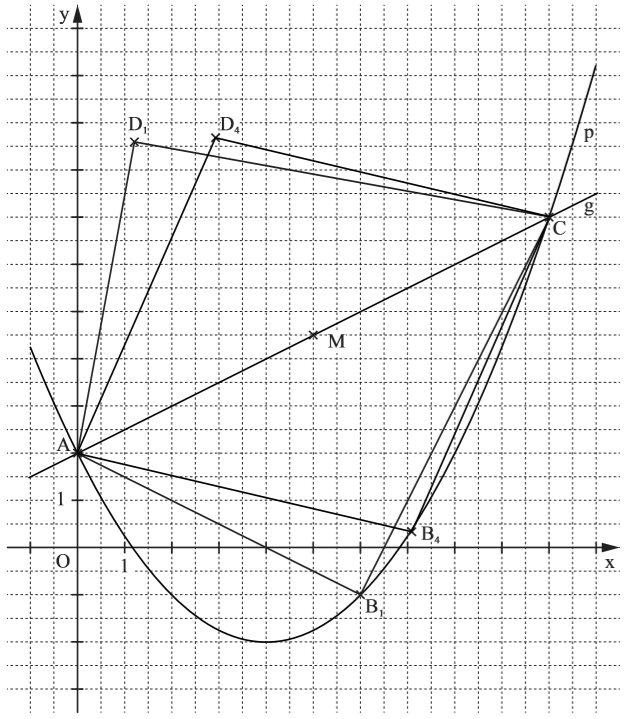
Zurück zum MAP-Hack:

Lösung zu B1.3
Zwei Gerade sind genau dann senkrecht aufeinander, wenn die Multiplikaton ihrer Steigungen -1 ergibt (\( m_1 \cdot m_2 = -1 \)). Aus den gegeben Punkten berechnest du die Steigungen und überprüfst die Rechtwinkligkeit an dieser Eigenschaft.
\begin{align} & \text{Berechnung der Steigungen}: \\
&A(0|2) \, ; \, B_1(6|-1) \, ; \, C(10|7): \\
m_{AB_1} &= \frac{\, y_B \, – \, y_A \,}{x_B \, – \, x_A} \\
&= \frac{\, -1 \, – \, 2 \,}{6 \, – \, 0} \\
\Rightarrow &m_{AB_1} = – 0,5 \\
\\
m_{B_1C} &= \frac{\, y_C \, – \, y_B \,}{x_C \, – \, x_B} \\
&= \frac{\, 7 \, – \, (-1) \,}{10 \, – \, 6} \\
\Rightarrow &m_{AB_1} = 2 \\
\\
&\text{Überprüfung der Eigenschaft:}\\
m_{AB_1} \cdot m_{B_1 C} &= -0,5 \cdot 2 = -1 \\
\Rightarrow &\text{Die Geraden stehen senkrecht, bei } B_1\end{align}

Lösung zu B1.4
Weil die Punkte auf der x-Achse liegen, gilt y = 0. Damit lassen sich über die Parabelgleichung die x-Werte bestimmen:
\begin{align} y &= 0,25x^2 – 2x + 2 \, \, \, \text{mit } y = 0 \\
0 &= 0,25x^2 -2x + 2 \\
\Rightarrow &\text{GTR: } x_2 = 1,17 \, \lor \, x_3 = 6,83\\
\Rightarrow &B_2(1,17|0) \, ; \, B_3(6,83|0) \end{align}
Zurück zum MAP-Hack:

Lösung zu B1.5
Das Drachenviereck lässt sich in zwei kongruente Dreiecke ABC zerlegen. Den Flächeninhalt dieser Dreiecke lässt sich über die Determinante bestimmen.
Leider kann ich aktuell noch keine Vektoren in LaTex formatieren. Wer mir da helfen kann, darf mir gerne ein Feedback schreiben. Solang gibt es die Lösung vom ISB:
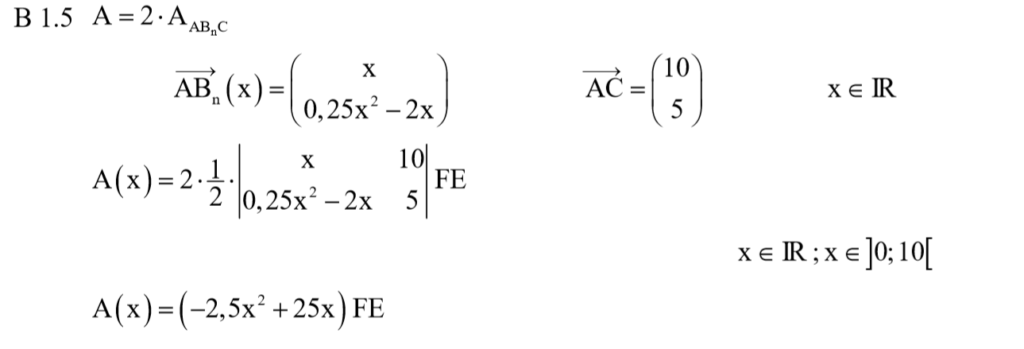
Zurück zum MAP-Hack:

Lösung zu B1.6
Bei einer Raute stehen die Diagonalen im Mittelpunkt senkrecht aufeinander. Über diese Eigenschaft lässt die die Aufgabe lösen. Aus der Eigenschaft, dass die Geraden senkrecht stehen bestimmst du die Steigung und setzt dann den Mittelpunkt in die Punkt-Steigungs-Form ein und löst auf.
\begin{align} &\text{Berechnung von M:} \\
M&(\frac{\,x_A \, + \, x_C\,}{2} \, | \,\frac{\, y_A \, + \, y_C}{2})\\
M&(\frac{\,0 \, + \, 10 \,}{2} \,| \, \frac{\, 2 \, + \, 7\,}{2}) \\
M&(5 \, | \, 4,5) \\
\\
&\text{Berechnung der Steigung:}\\
m \cdot m_g &= -1 \\
m \cdot 0,5 &= -1 \, \, |:0,5 \\
\Rightarrow &m = -2 \\
\\
&\text{Einsetzen in die PS-Form}: \\
y &= m \cdot (x – x_M) + y_M \,\,\ \text{mit }M(5\, | \, 4,5)\text{ und } m = -2 \\
y &= -2 \cdot (x – 5) + 4,5 \\
\Rightarrow y&=-2x + 14,5 \end{align}

Ich habe eine Frage zu 1.2…wenn der Punkt B aber bis zur Null wandert und sich mit A schneidet, gäbe es doch keine Drachenvierecke mehr, sondern Dreiecke, oder? Also müsste das Intervall nicht bei 0,1 oder 0,5 oder so beginnen?😅
Hallo,
schön, dass du fragst. Du hast das Problem komplett verstanden. Bei x = 0 haben wir ein Problem, aber jede Zahl größer als 0 ist erlaubt. 0,1 oder 0,01 oder 0,001 …
Dass die Zahl beliebt nah an 0 sein darf, aber eben nicht 0 selbst, dafür macht man die Klammer, die von der 0 wegdeutet. Also ]0
Danke! Ich habe dann auch verstanden, dass wir deshalb diese Klammer verwenden.
Ich habe morgen meine Prüfung, hoffentlich schaffe ich es! 🙂
Liebe Grüße