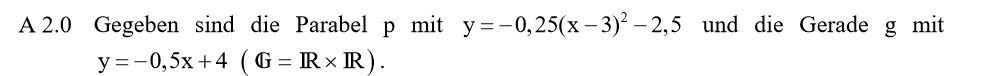
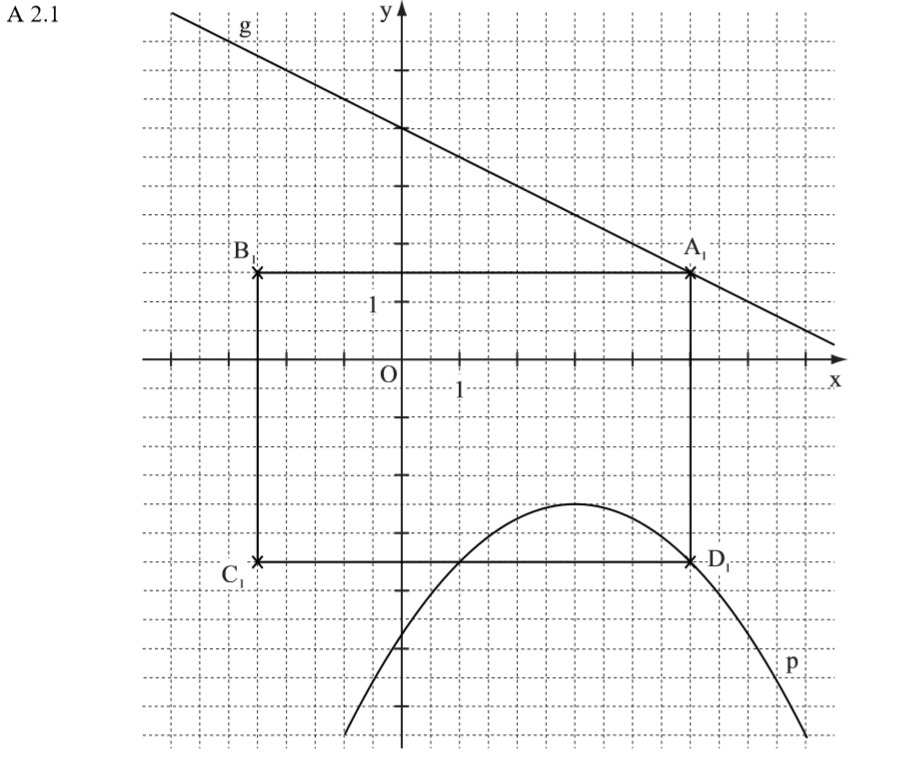
Lösung zu A2.1
\begin{align} y &= -0,25 \cdot (x – 3)^2 – 2,5 \\
&= -0,25 \cdot (x^2 -6x + 9) – 2,5 \\
&= -0,25x^2 + 1,5x – 2,25 -2,5 \\
\Rightarrow &y = -0,25x^2 + 1,5x -4,75 \end{align}
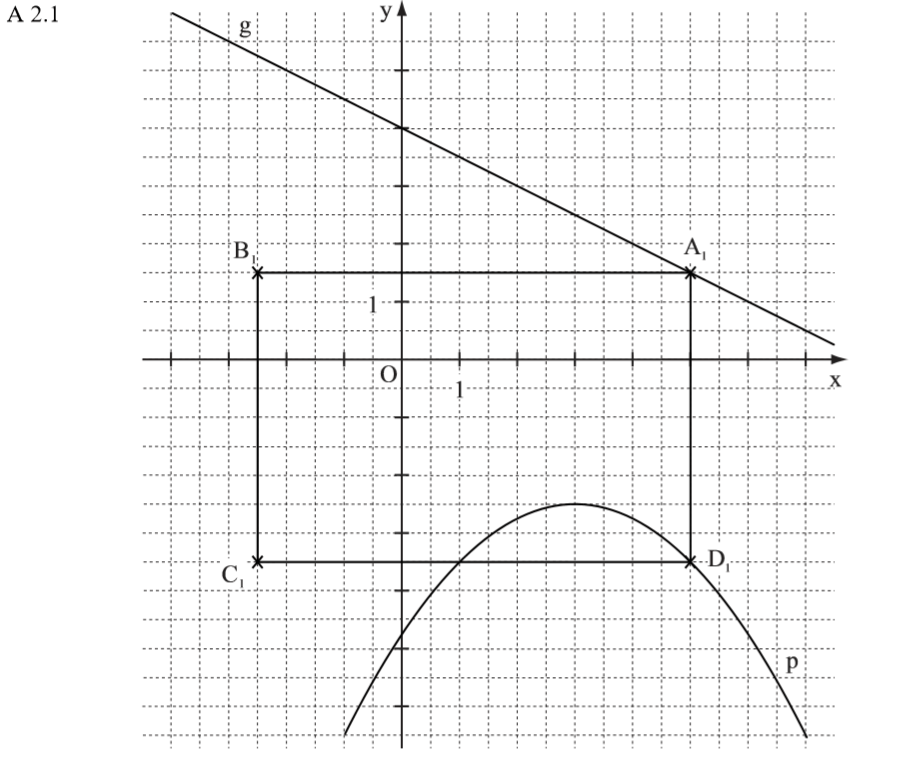
Zurück zum MAP-Hack:

Lösung zu A2.2
Zurück zum MAP-Hack:

Lösung zu A2.3
\begin{align} &\overline{AD} \, \text{durch „Oben – Unten“:}\\
\overline{AD} &= y_A – y_D \\
&= -0,5x + 4 – (-0,25x^2 + 1,5 – 4,75) \\
&= -0,5x + 4 + 0,25x^2 – 1,5x + 4,75 \\
\Rightarrow &y = (0,25x^2 – 2x + 8,75) \text{LE} \\
\\
&\text{Berechnung des Umfangs:}\\
u &= 2 \cdot (\overline{AD} + \overline{AB})\\
&= 2 \cdot (\overline{AD} + 1,5 \cdot \overline{AD})\\
&= 2 \overline{AD} + 3 \cdot \overline{AD}\\
&= 5 \cdot \overline{AD} \\
&= 5 \cdot (0,25x^2 -2x + 8,75) \\
\Rightarrow &u = (1,25x^2 – 10x + 43,75) \text{LE} \end{align}
Zurück zum MAP-Hack:
Lösung zu A2.4
\begin{align} u(x) &= 28,75 \\
1,25x^2 -10x + 43,75 &= 28,75 \, \, \, | – 28,75 \\
1,25x^2 -10x +15 &= 0 \\
\Rightarrow GTR \Rightarrow x = 2 \, \lor \, x = 6 \end{align}
Zurück zum MAP-Hack:

Lösung zu A2.5
Die Seiten \( \overline{AD} \text{ und } \overline{AB} \) sind über die Formel \( \overline{AB} = 1,5 \cdot \overline{AD} \) miteinander verknüpft. Verdoppelt sich die eine Seite, verdoppelt sich also auch die andere. Insgesamt vervierfacht sich also der Flächeninhalt. Die Fläche steigt auf 400%, also ist sie um 300% größer.
