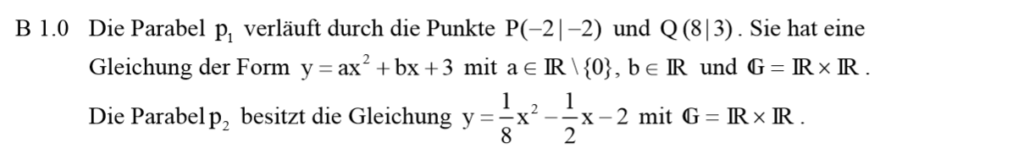

Lösung zu B1.1
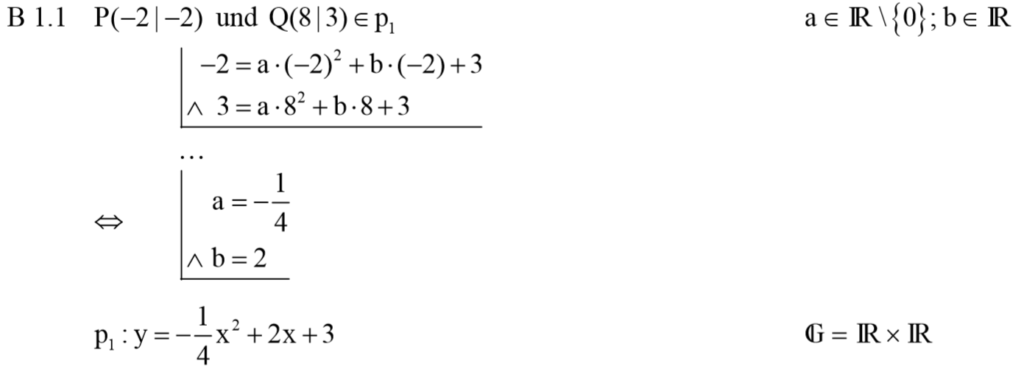
Zurück zum MAP-Hack:

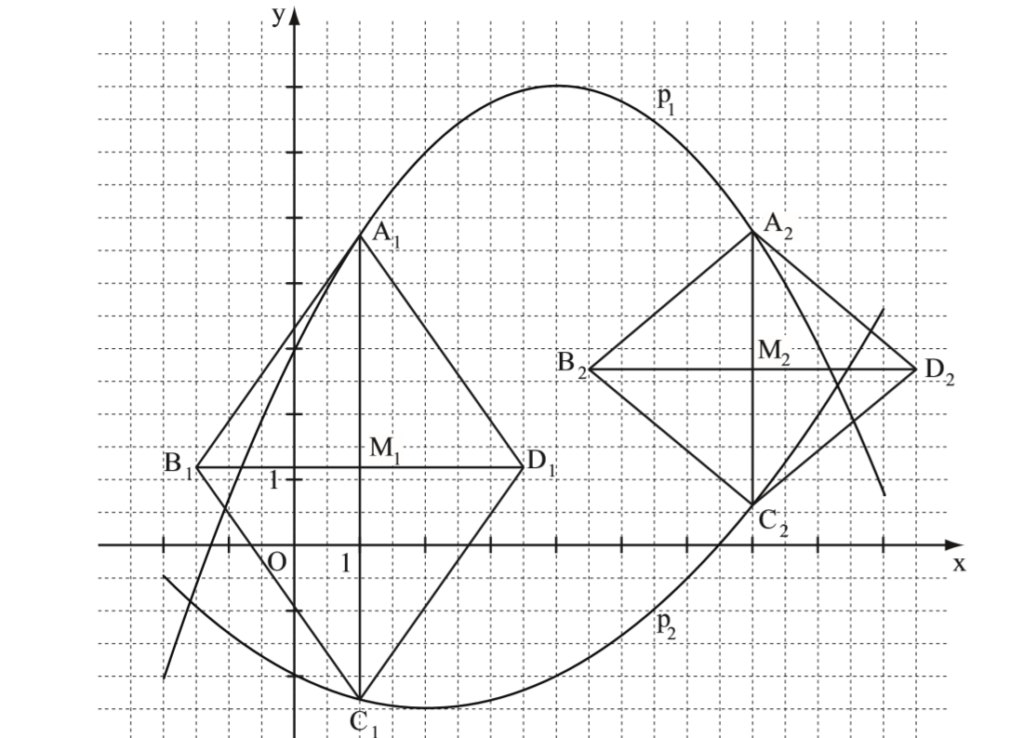
Lösung zu B1.2
Zurück zum MAP-Hack:

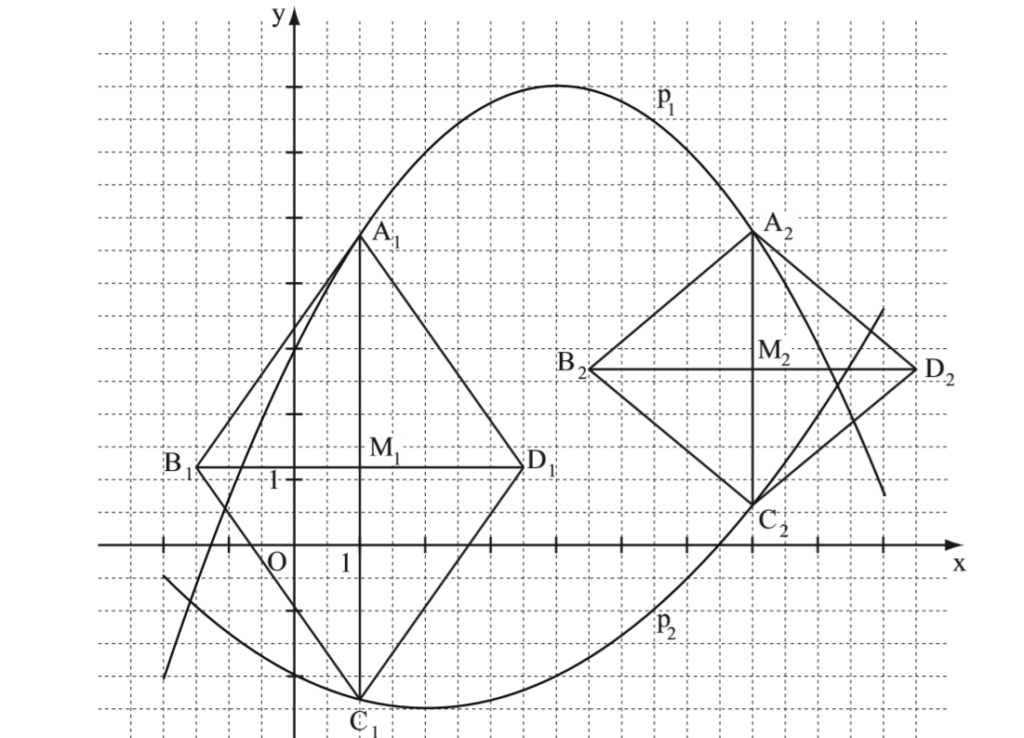
Lösung zu B1.3
Die Punkte A und C haben die selbe Abszisse, also darfst du die Formel „Oben – Unten“ verweden. Die y-Werte der Punkte sind jeweils die Funktionsterme der Parabeln.
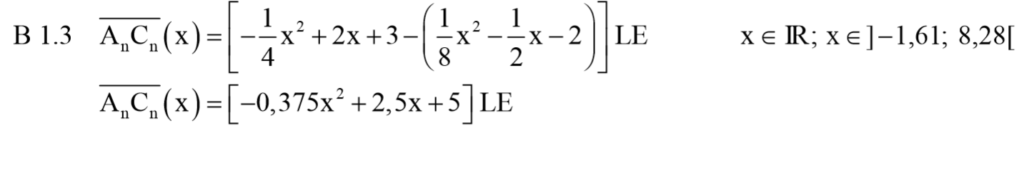
Zurück zum MAP-Hack:

Lösung zu B1.4
Der Ansatz geht über den Satz des Pythagoras, weil das Dreieck ABM rechtwinklig bei M ist. Damit kann die Länge der Strecke [AM] bestimmt werden. [AC] ist doppelt so lang wie [AM] und für [AC] kennen wir die Formel aus 1.3 Du kannst also eine quadratische Gleichung aufstellen und die beiden Werte für x ausrechnen.
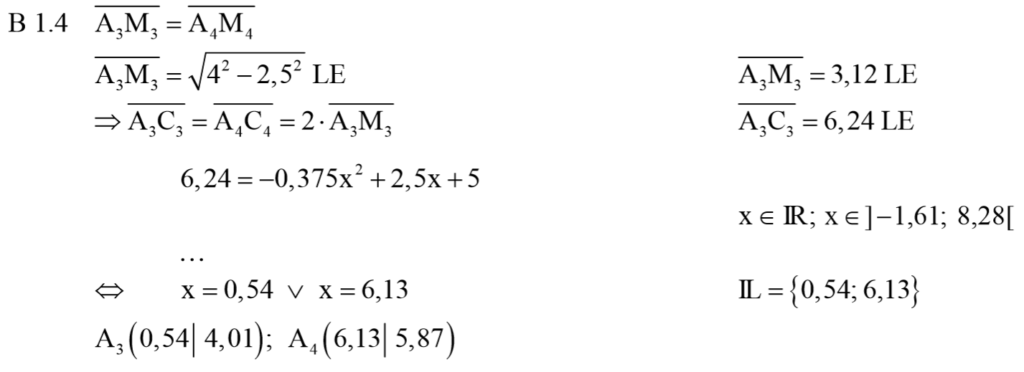
Zurück zum MAP-Hack:

Lösung zu B1.5
Berechne mit deinem Taschenrechner den Maximalwert der quadratischen Gleichung aus 1.3. Danach verwendest du die Flächenformel der Raute, um diesen zu bestimmen.

Zurück zum MAP-Hack:

Lösung zu B1.6
Eine Erklärung zum Argumentieren für größte bzw kleinste Winkel gibt es im MAP-Hack: Raumgeometrie.

