Quadratische Funktionen
1.1
Es sind zwei Punkte P und Q gegeben, also arbeitest du mit einem Gleichungssystem
\begin{align} &\text{P in p:}\\
(1) y &= ax² + bx + 3 \\
-2 &= a \cdot (-2)^2 + b \cdot (-2) + 3 \\
-2 &= 4a – 2b + 3 \,\,\, |-3 \\
-5 &= 4a – 2b \\
\\
&\text{Q in p:}\\
(2) y &= ax² + bx + 3 \\
3 &= a \cdot 8^2 + b \cdot 8 + 3 \,\,\, |-3 \\
0 &= 64a + 8b \\
\\
GTR &=\Rightarrow a = -0,25 \, ; \, b = 2 \\
&\Rightarrow y = -0,25x² + 2x + 3 \end{align}
1.2 + 1.3
1.4
Um die Schnittpunkte zu berechnen, setzt du die Parabelterme gleich und löst die Gleichung mit deinem Taschenrechner.
\begin{align}
y_{p_1} &= y_ {p_2} \\
-0,25x² + 2x + 3 &= 0,125x² – 0,5x – 2 \,\,\, |-0,125x² + 0,5x + 2 \\
-0,375x² +2,5x + 5 &= 0 \\
&\Rightarrow Taschenrechner: x_1 = 8,28 \, ; \, x_2 = -1,61 \\
&\Rightarrow x \in ]-1,61 ; 8,28[ \end{align}
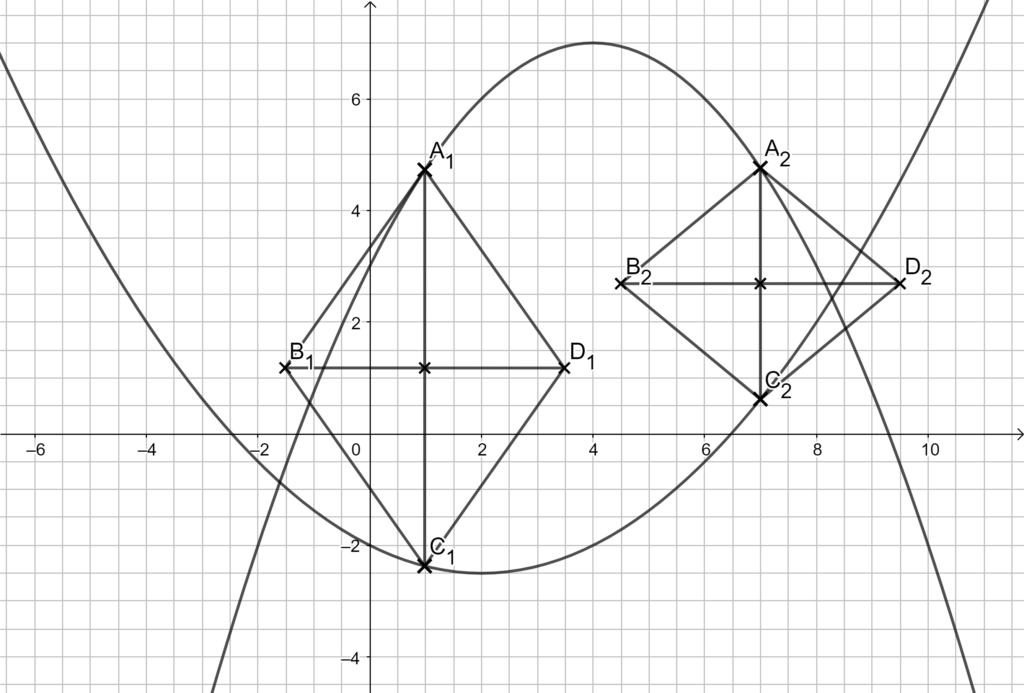
1.5
Den Flächeninhalt einer Raute bestimmst du mit der Formel \(A = 0,5 \cdot e \cdot f \).
Die Diagonalen sind hier \( |\overline{A_n C_n}| \) und \(|\overline{Bn Dn}|\).
Laut Angabe gilt \(\overline{Bn Dn} = 5 \) und weil A und C dieselbe Abszisse x haben, kannst du die Streckenlänge durch „Oben – unten“ bestimmen.
\begin{align} &|\overline{An Cn}| \text{ durch „oben – unten“:}\\
|\overline{An Cn} (x)| &= y_A – y_c \\
&= -0,25x² + 2x + 3 – (0,125x² – 0,5x – 2) \\
&= -0,25x² + 2x + 3 – 0,125x² + 0,5x + 2 \\
\Rightarrow &|\overline{A_n C_n}(x)| = -0,375x² +2,5x + 5 \\
\\
&\text{ Berechnung der Rautenfläche über die Flächenformel}\\
A(x) &= 0,5 \cdot |\overline{A_n C_n}| \cdot |\overline{Bn Dn}| \\
&= 0,5 \cdot (-0,375x² +2,5x + 5) \cdot 5 \\
&= 2,5 \cdot (-0,375x² +2,5x + 5) \\
&\Rightarrow A(x) = (- 0,9365x² + 6,25x + 12,5) FE \\
&= \text{ gerundet: } A(x) = (-0,94x² + 6,25x + 12,5) FE \end{align}
1.6
Eine Raute ist genau dann ein Quadrat, wenn die Diagonalen gleiche Länge haben. Mit dieser Info lässt sich eine Gleichung aufstellen und lösen.
\begin{align}
|\overline{A_n C_n}| &= |\overline{Bn Dn}| \\
-0,375x² +2,5x + 5 &= 5 \,\,\, |-5 \\
-0,375x² +2,5x &= 0 \\
&\Rightarrow Taschenrechner x_1 = 6,67 ; x_2 = 0
\end{align}
Für 6,67 und 0 sind die Rauten gleichzeitig Quadrate.
1.7
Der Winkel \( \angle An Dn Mn \) hat sein größtes Maß, wenn die Diagonale [A_n C_n] ihre maximale Länge erreicht.
Du kannst die längste Diagonale mit deinem Taschenrechenr bestimmen: x = 3,33 mit \( |\overline{A_0 C_0}| \) = 9,17.
Im Dreieck AMD mit der halben Diagonale [AM] kannst du mit dem Tangens diesen größten Winkel ausrechnen.
\begin{align} \\
tan{angle A_0 D_0 M_0 } &= \frac{|\overline{AM}|}{|\overline{MD}|} \\
&= \frac{4,59}{2,5} \,\,\, |tan^{-1}\\
&\Rightarrow \angle A_0 D_0 M_0 = 61,42° \end{align}
Der größte auftretende Winkel ist 61,42°, also kleiner als 65°.
Ebene Geometrie
1.1
Um die Streckenlängen zu erhalten, in denen du zeichnest, rechnest du zuerst die Meter in Zentimeter um (mal 100) und teilst dann durch den Maßstab (:500).
\begin{align} |\overline{AB}| &= 60m = 6000 cm \Rightarrow 12 cm. \\
|\overline{AC}| &= 11,6 cm \\
|\overline{AD}| &= 8 cm \end{align}
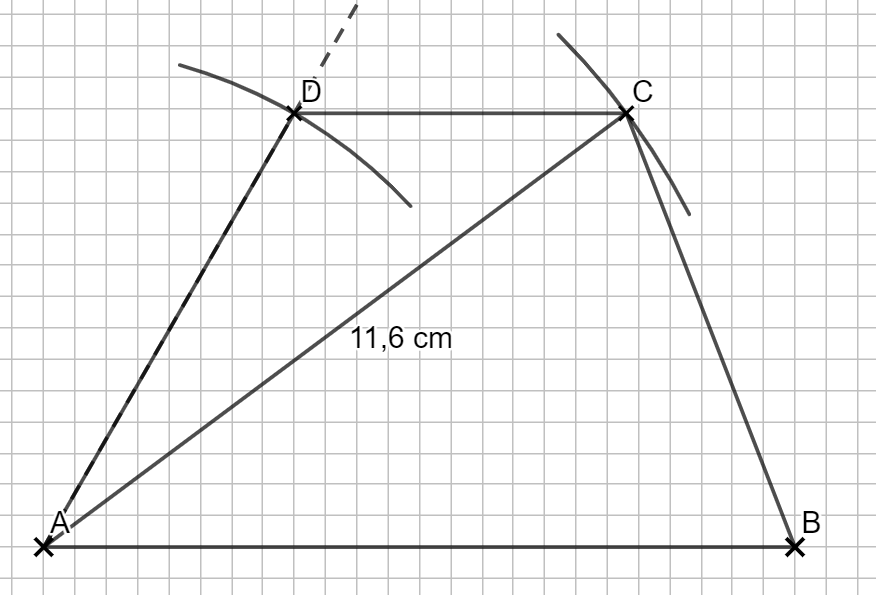
1.2 \begin{align} &\angle DCA \text{ mit dem Sinussatz:}\\
\frac{sin(\angle DCA)}{|\overline{AD}|} &= \frac{sin(\angle ADC)}{|\overline{AC}|} \,\,\, |\cdot |\overline{AD}|\\
sin(\angle DCA) &= \frac{sin(\angle ADC)}{|\overline{AC}|} \cdot |\overline{AD}| \\
&= \frac{sin(180° – 60°)}{58} \cdot 40 \,\,\, |sin^{-1}\\
&\Rightarrow \angle DCA = 36,67° \\
&d(\overline{AB} \, ; \, \overline{CD}) \text{ mit dem Sinus:}\\
sin(\angle BAD) &= \frac{d(\overline{AB} \, ; \, \overline{CD})}{|\overline{AD}} \,\,\, |\cdot |\overline{AD}|\\
&\Rightarrow d(\overline{AB} \, ; \, \overline{CD}) = sin(60°) \cdot 40 = 34,64 m. \end{align}
1.3
Der gesuchte Winkel ACB ist Teil des Dreiecks ABC. Leider hast du hier nur zwei Angaben. Der erste Trick ist nicht ganz einfach zu sehen.
Der Winkel BAC ist ein Weckselwinkel zu DCA und damit 36,67°. Das funktioniert nur, weil AB parallel zu CD ist.
Jetzt hat du drei Angaben im Dreieck ABC, kannst aber den Winkel nicht direkt bestimmen. Zuerst musst du die Streckenlänge \( |\overline{BC}|\) mit dem Cosinussatz bestimmen.
Ja, diesen Weg zu finden ist nicht einfach, so sind diese Aufgaben leider. Wenn du mal nicht weiterkommst, dann achte auf die Zwischenergebnisse. Sie sind ein Hinweis darauf, wie gerechnet werden kann.
\begin{align} &|\overline{BC}| \text{ mit dem Cosinussatz:}\\
|\overline{BC}^2| &= |\overline{AB}|^2 + |\overline{BC}|^2 – 2 \cdot |\overline{AB}| \cdot |\overline{BC}|\cdot cos(\angle BAC) \\
&= 60^2 + 58^2 – 2 \cdot 60 \cdot 58 \cdot cos (36,67°) \,\,\, |\sqrt{} \\
&\Rightarrow |\overline{BC}| = 37,17 \\
\\
&\angle ACB \text{ mit dem Sinussatz:}\\
\frac{sin(\angle ACB)}{|\overline{AB}|}&= \frac{sin(\angle BAC)}{|\overline{BC}|} \,\,\, |\cdot |\overline{AB}|\\
sin(\angle ACB) &= \frac{sin(\angle BAC)}{|\overline{BC}|} \cdot |\overline{AB}|\\
&= \frac{60 \cdot sin(36,67°)}{37,17} \,\,\, |sin^{-1} \\
&\Rightarrow \angle ACB = 74,58° \end{align}
1.4
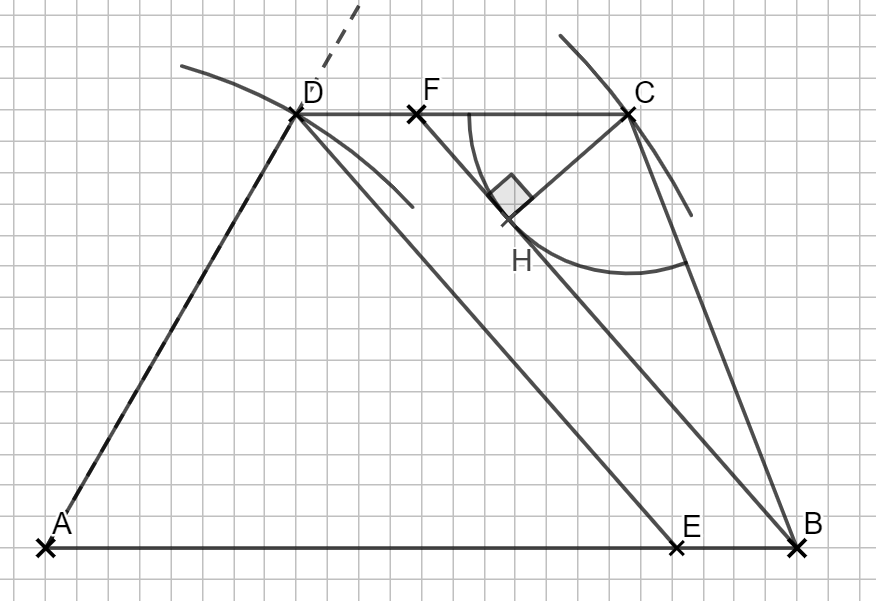
Für die Flächenformel des Kreissektors benötigst du den Innenwinkel, den du leicht durch Addition von DCA und ACB bekommst.
Beim Radius des Kreises kommt die Eigenschaft mit dem Berührpunkt ins Spiel. \( \overline{CH} \) steht senkrecht, weil H ein Berührpunkt ist.
Du kennst aus der Aufgabenstellung den Winkel bei B und zusammen mit der Streckenlänge \( |\overline{BC}|\) kannst du mit dem Sinus ansetzen.
\begin{align} &r = |\overline{CH}| \text{ mit dem Sinus:}\\
sin(\angle CBF) &= \frac{|\overline{CH}|}{|\overline{BC}|} \,\,\, |\cdot |\overline{BC}| \\
|\overline{CH}| &= sin(\angle CBF) \cdot |\overline{BC}| \\
&= sin(20°) \cdot 37,17 m \\
&\Rightarrow |\overline{CH}| = 12,71 m \end{align}
1.5
Der Flächeninhalt des Parallelgramms berechnet sich durch \( A = g \cdot h \). Hier ist die Grundseite \( \overline{BE} \) und die Höhe \( d(\overline{AB} \, ; \, \overline{CD}) \) kennst du schon aus 1.2.
Die Grundseite darfst du messen. Es sind 5,3 cm, was mit 500 multipliert und durch 100 geteilt 26,5 m ergibt.
Jetzt musst du nurnoch einsetzen.
\begin{align} &A_{Sektor} \text{ mit der Flächenformel:}\\
A_{Sektor} &= \frac{\angle DCB}{360°} \cdot |\overline{CH}|^2 \cdot \pi \\
&= \frac{112,25°}{360°} \cdot 12,71^2 \cdot \pi \\
&\Rightarrow A_{Sektor} = 158,24 m^2 \\
&\Rightarrow V_1 = A_{Sektor} \cdot 0,18 = 28,48 l \\
\\
A_{Parallelogramm} &= |\overline{BE}| \cdot d(\overline{AB} \, ; \, \overline{CD}) \\
&= 26,5 \cdot 34,64 \\
&\Rightarrow A_{Parallelogramm} = 917,96 m^2 \\
&\Rightarrow V_2 = A_{Parallelogramm} \cdot 0,18 = 165,23 l \end{align}
