2022 Haupttermin B2: Raumgeometrie

\begin{align} &|\overline{FM} \text{ mit dem Satz des Pythagoras:}\\
|\overline{FM}|^2 &= |\overline{CM}|^2 + |\overline{CF}|^2 \\
&= 8^2 + 11^2 \,\,\, |\sqrt{}\\
\Rightarrow &|\overline{FM}| = 13,60 cm \\
\\
&\angle CFM \text{ mit dem Tangens:}\\
tan(\angle CFM) &= \frac{|\overline{CM}|}{|\overline{CF}|}\\
&= \frac{8}{11} \,\,\, |tan^{-1}\\
\Rightarrow &\angle CFM = 36,03° \end{align}

\begin{align} &A_{CPF} \text{ mit der Sinus-Formel:}\\
A_{CPF} &= 0,5 \cdot |\overline{CF}| \cdot |\overline{FP_1} | \cdot sin(\angle CFM)\\
&= 0,5 \cdot 11 \cdot 4 \cdot sin(36,03°) \\
\Rightarrow &A_{CPF} = 12,94 cm^2 \\
\\
&|\overline{CP_1}| \text{ mit dem Cosinussatz:}\\
|\overline{CP_1}|^2 &= |\overline{FP_1}|^2 + |\overline{CF}|^2 – 2 \cdot |\overline{FP_1}| \cdot |\overline{CF}| \cdot cos(\angle CFM) \\
&= 4^2 + 11^2 – 2 \cdot 4 \cdot 11 \cdot cos(36,03°) \,\,\, |\sqrt{}\\
\Rightarrow &|\overline{CP_1}| = 8,11 cm \end{align}

Für die Volumenformel benötigst du die Grundfläche und die Höhe. Die einfachen Dinge zuerst:
\begin{align} &A_g \text{ mit der Dreiecksformel:}\\
A_g &= 0,5 \cdot |\overline{AB}| \cdot |\overline{MC}|\\
&= 0,5 \cdot 10 \cdot 8 \\
\Rightarrow &A_g = 40 cm^2 \end{align}

Diese Aufgabe könnte man mit dem Vierstreckensatz lösen, weil FC parallel zu PK ist. Hier würde ich – aber das ist mein persönliches Ding – über Sin, Cos, Tan gehen, indem man im Dreieck CMF den Winkel bei M berechnet.

\begin{align} &\angle FMC \text{ über die Innenwinkelsumme:}\\
\angle FMC &= 180° – 90° – 36,03° = 53,97° \\
\\
&|\overline{MP_n} | \text{ mit dem Sinus:}\\
sin(\angle FMC) &= \frac{|\overline{P_n K_n}|}{|\overline{MP_n} |} \\
sin(53,97°) &= \frac{|\overline{P_n K_n}|}{13,60 – x}\,\,\, |\cdot (13,60 – x) \\
sin(53,97°) \cdot (13,60 – x ) &= |\overline{P_n K_n}|\\
0,81 \cdot (13,60 – x ) &= |\overline{P_n K_n}|\\
\Rightarrow &|\overline{P_n K_n}| = 11,01 – 0,81x \\
\\
& \text{Einsetzen in die Volumenformel:}\\
V(x) &= \frac{1}{3} \cdot A_g \cdot |\overline{P_n K_n}| \\
&= \frac{1}{3} \cdot 40 \cdot (11,01 – 0,81x) \\
&= \frac{1}{3} \cdot (440,4 – 32,4x) \\
&\Rightarrow V(x) = (146,80 – 10,80x) cm^3 \end{align}
Aufgrund von Rundungen in Zwischenschritten ergibt sich das Ersatzergebnis nicht exakt

Ziel der Aufgabe ist es, das funktionale Volumen mit 15% des Prismavolumens gleichzusetzen. Dafür musst du zuerst das Prismavolumen bestimmen.
\begin{align} V_{Prima} &= A_g \cdot |\overline{CF}|\\
&= 40 \cdot 11 \\
V_{Prisma}&= 440 cm^3 \\
\\
V(x) &= 0,15 \cdot V_{Prisma}\\
146,67 – 10,80x &= 0,15 \cdot 440 \, \, \ |-146,67 \\
-10,80x &= -80,67 \,\,\, |:(-10,80)\\
x &= 7,47 \end{align}

Das Stichwort „kürzeste Entfernung“ gibt dir den Hinweiß, dass bei P0 ein rechter Winkel im Dreieck CMP0 ist. Mit dieser Eigenschaft und dem Geodreieck kann du P0 einzeichnen.

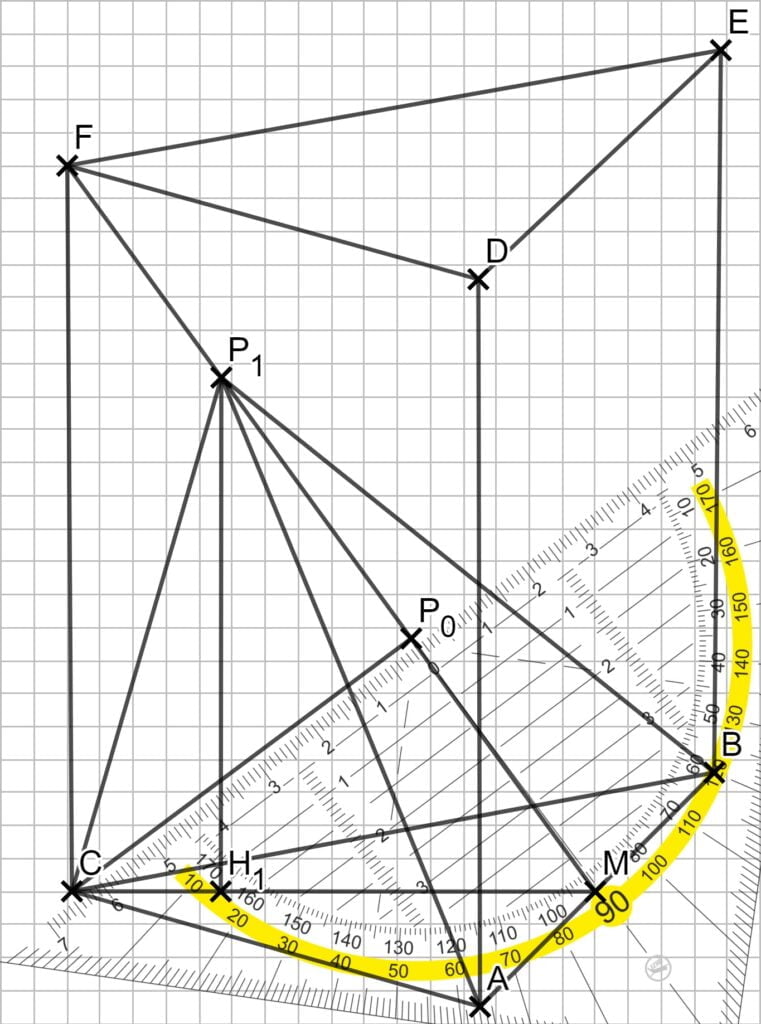
Im Dreieck CMP0 kannst du mit dem rechten Winkel die Streckenlänge MP0 ausrechnen.
\begin{align} &|\overline{MP_0}| \text{ mit dem Cosinus:}\\
cos(\angle FMC) &= \frac{|\overline{MP_0}|}{|\overline{CM}|}\\
cos(53,97°) &= \frac{|\overline{MP_0}|}{8} \,\,\, |\cdot 8\\
\Rightarrow &|\overline{MP_0}|= 4,71 cm \end{align}

Jetzt hast du im Dreieck AMP0 drei Angaben, weil du weißt, dass bei M ein rechter Winkel ist.
\begin{align} &\angle AP_0M \text{ mit dem Tangens:}\\
tan(\angle AP_0M) &= \frac{|\overline{AM}|}{|\overline{MP_0}|} \\
&= \frac{5}{4,71} \,\,\, |tan^{-1}\\
\angle AP_0M &= 46,71° \\
\\
\angle AP_0B = 2 \cdot 46,71° &= 93,42° \end{align}