

Lösungen zu B1.1
Die Berechnung der Parabelgleichung in dieser Aufgabe ist einzigartig. Nur hier brauchst du dieses Vorgehen. Manche Dinge bleiben aber gleich: Es ist der Scheitelpunkt gegeben, also verwendest du die Scheitelform \( y = a \cdot (x – x_s)^2 + y_s \). Dort setzt du für \(x_s\) und \(y_s\) die Koordinaten des Scheitelpunkts ein. Wenn du jetzt für x und y die Koordinaten von P einsetzt, so erhälst du eine Gleichung, in der du nur a nicht kennst. Du kannst sie also nach a auflösen und diesen Wert bestimmen (a = -0,25). Diesen setzt du jetzt statt P in die Scheitelform ein, löst die Klammer mit einer binomischen Formel auf und vereinfachst soweit wie möglich.
\begin{align} &S(4|2) \in p : \\ y &= a \cdot (x – x_s) ^2 + y_s \\ y &= a \cdot (x – 4)^2 + 2 \\ \\ &P(-2|-7) \in p : \\ -7 &= a \cdot (-2 – 4)^2 + 2 \\ -7 &= a \cdot (-6)^2 + 2 \, \, \, -2 \\ -9 &= a \cdot 36 \,\,\, |:36 \\ \Rightarrow &a = -0,25 \\ \\ y = -0,25 \cdot (x-4)^2 +2 \\ &= 0,25 \cdot (x – 8x + 16)^2 + 2 \\ &= -0,25x^2 +2x – 4 + 2 \\ \Rightarrow &y = -0,25x^2 -2x -2 \end{align}
Zurück zum MAP-Hack:

Lösung zu B1.2

Zurück zum MAP-Hack:
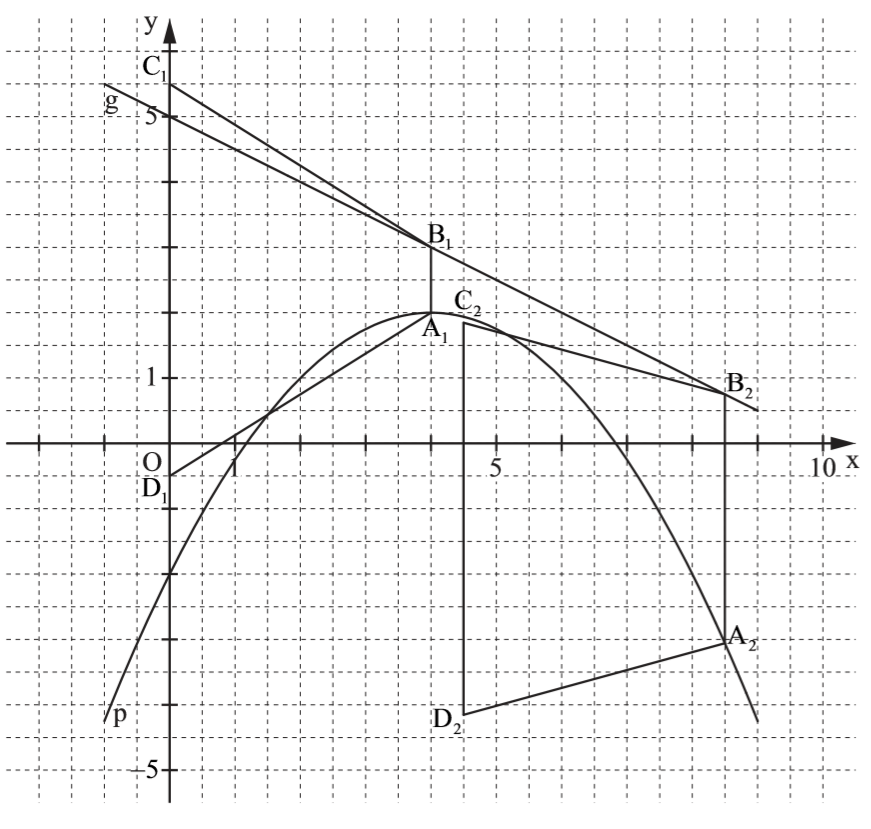
Lösung zu B1.3
Für die Flächenfolgen des Trapezes (\(A_{Trapez} = 0,5 \cdot (a + c) \cdot h) \)) benötigst du die Länge der Strecke \( \overline{A_n B_n} \). Weil A und B die selbe Abszisse haben, kannst du „oben – unten“ verwenden.
\begin{align} &\overline{A_n B_n} \, mit \, \, „oben \, \, – \, unten“: \\ \overline{A_n B_n} &= y_{Gerade} – y_{Parabel} \\ &= -0,5x + 5 – (-0,25x^2 +2x – 2) \\ &= 0,25x^2 -2,5x +7 \\ \\ &Einsetzen \, in \, die \, Flächenformel: \\ A_{Trapez} &= 0,5 \cdot (\overline{A_n B_n} + \overline{C_n D_n}) \cdot h \\ &= 0,5 \cdot (0,25x^2 – 2,5x + 7 + 6 ) \cdot 4 \\ \Rightarrow &A_{Trapez} = 0,5x^2 – 5x +26 \end{align}

Lösung zu B1.4
Du löst die Aufgabe, indem du die Formel \( A(x) = 0,5x^2 – 5x + 26 \) in den GTR eingibst und den Extremwert bestimmst. Der minimale Flächeninhalt A = 13,5 FE für x = 5.

Lösung zu B1.5
\begin{align} & x \, über \, eine \, quadratische \, Gleichung: \\ 0,5x^2 -5x + 26 &= 25 \, \, \, |-25 \\ 0,5x^2 -5x +1 &= 0 \\ \Rightarrow >R \Rightarrow x = 0,20 \lor x = 9,80 \end{align}
Wenn die Trapeze Rechtecke wären, müssen sie die Eigenschaften des Rechtecks erfüllen. Gegenüberliegende Seiten müssen also gleich-lang und der Flächeninhalt muss sich durch Länge mal Breite berechnen lassen. Weil 6 mal 4 aber 24 ergibt und nicht 25, sind es keine Rechtecke. Die Flächenformel ist nicht erfüllt.
Lösung zu B1.6
\begin{align} &\overline{A_1 B_1} \, mit \, Funktionsgleichung: \\ \overline{A_1 B_1} &= f(4) = 0,25 \cdot 4^2 – 2,5 \cdot 4 + 7 = 1 LE \\ \\ &\epsilon \, mit \, dem \, Tangens: \\ tan(\epsilon) &= \frac{h}{0,5 \cdot (\overline{C_1 D_1} – \overline{A_1 B_1})}\\ &= \frac{4 }{0,5 \cdot (6 – 1)} \\ \Rightarrow &\epsilon = 57,99° \end{align}
