Bei Aufgaben zu den quadratischen Funktionen muss manchmal neben der Parabel in der ersten Teilaufgabe auch eine Gerade eingezeichnet werden. Auf dieser Seite erkläre ich dir zwei Möglichkeiten eine Gerade zu zeichnen. Welche dir besser gefällt, darfst du dann selbst entscheiden =) .
Lineare Funktionen – Die Basics
Eine Geradengleichung hat die Form \( y = m \cdot x \, + \, t \).
Dabei ist m die Steigung und t der y-Achsenabschnitt.
Ich erkläre das Beispiel anhand der Funktion \( y = \frac{1}{3} \cdot x \, + 1 \).
Die Steigung ist \(m = \frac{1}{3} \), der y-Achsenabschnitt \( t = 1\)
Die Steigung m – Geht es hoch oder runter?
Ist die Steigung m größer als 0, steigt die Gerade. Sie läuft von „Unten links nach oben rechts“. Ist die Steigung kleiner als 0, dann ist es andersherum. Die Gerade fällt.
Bei einer Steigung von 0 ist die Gerade parallel zur x-Achse.
Die Steigung beschreibt, wie sehr sich der y-Wert verändert, wenn man an der x-Achse entlang läuft. In mathematischer Bezeichnung schreibt man:
\( m = \frac{\Delta y}{\Delta x} \)
Der y-Achsenabschnitt t – Wo fangen wir eigentlich an?
Jede Gerade schneidet die y-Achse. Der y-Achsenabschnitt t ist der Wert, bei der geschnitten wird. Du kannst also diesen Schnittpunkt am Funktionsterm \( y = m \cdot x \, + \, t \) direkt ablesen.
Methode 1: Über t und m
Um eine Gerade zu zeichnen, benötigst du zwei Punkte, die du dann mit deinem Lineal verbindest. Wir machen das Beispiel mit \( y = \frac{1}{3} \cdot x \, + 1\).
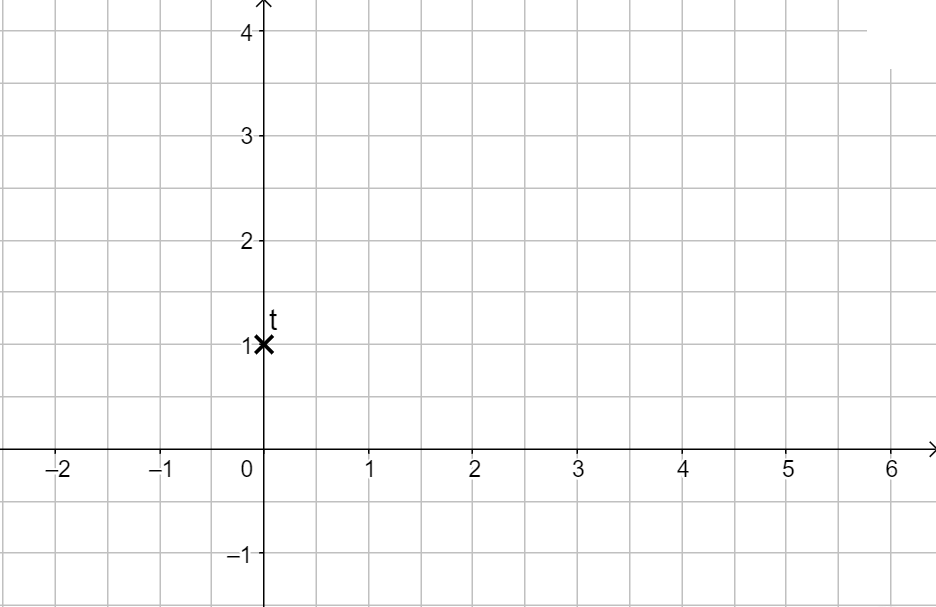
Den ersten Punkt findest du, indem du auf der y-Achse einfach den Wert t markierst. Das ist der erste Punkt… ja wirklich, es ist so einfach!
Der y-Achsenabschnitt ist \( t = 1 \), du markierst also an der y-Achse den Wert 1.
Bei der Steigung wird es etwas komplizierter. Zuerst schreibst du dir die Steigung als Bruch \( m = \frac{\Delta y}{\Delta x} = \frac{1}{3}\).
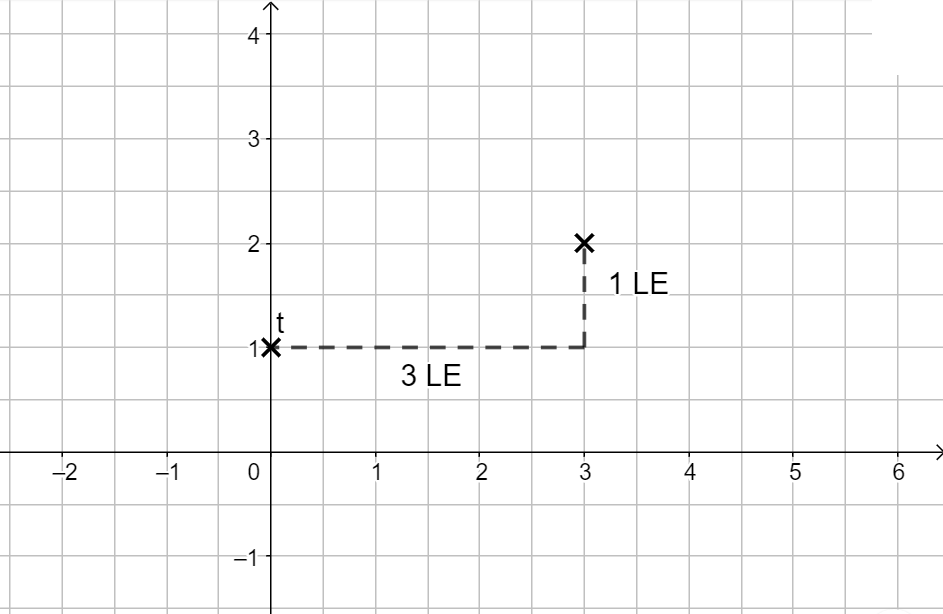
Jetzt hast du eine Wegbeschreibung zum zweiten Punkt! Gehe vom y-Achsenabschnitt aus den Nenner – hier 3 – in x-Richtung und den Zähler – hier 1 – in y-Richtung. Dort ist der zweite Punkt. Du kannst einzelne Kästen oder Längeneinheiten gehen, das macht keinen Unterschied.
Mein Tipp für dich:
Ist die Steigung eine ganze Zahl, zum Beispiel m = 2, dann schreib es trotzdem als Bruch mit Nenner 1: \( m = 2 = \frac{2}{1} \).
Schon hast du wieder deine Wegbeschreibung. Und zur Erinnerung die Umrechnung von Dezimalzahlen: \( 0,2 = \frac{2}{10} \)
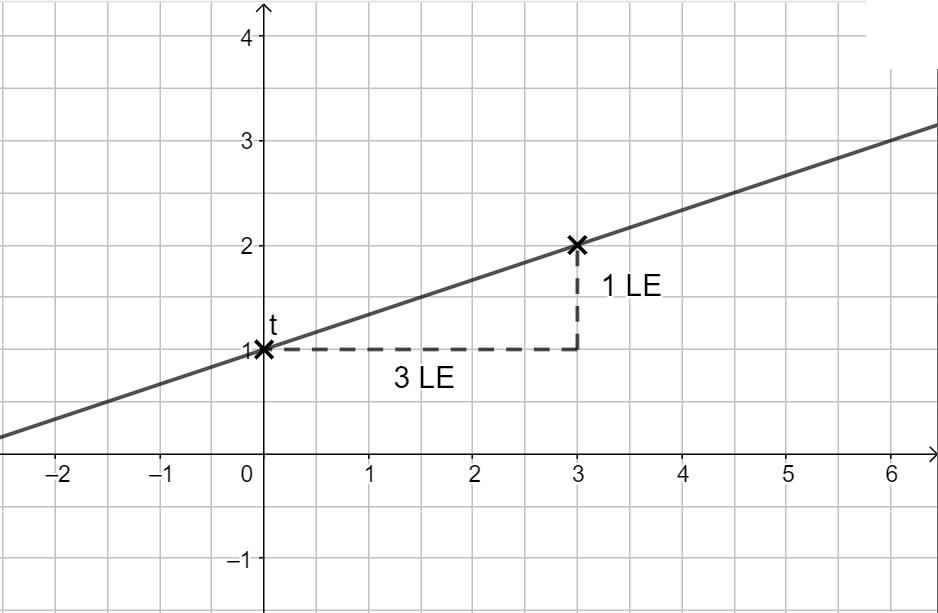
Jetzt musst du nurnoch die beiden Punkte verbinden und bist fertig.
Methode 2: Der Taschenrechner ist mein Freund
Der Funktionsterm ist die magische Verbindung zwischen x und y. Wünsche dir einen Wert für x, ich emfehle dir mit 0 anzufangen und gebe den Funktionsterm mit deinem gewählten Wert für x ein. Das Ergebnis des Taschenrechners ist der Wert für y und zusammen bilden sie einen Punkt. Diese kannst du einzeichnen. (Funktionsterm: \( y = \frac{1}{3} \cdot x \, + 1 \))
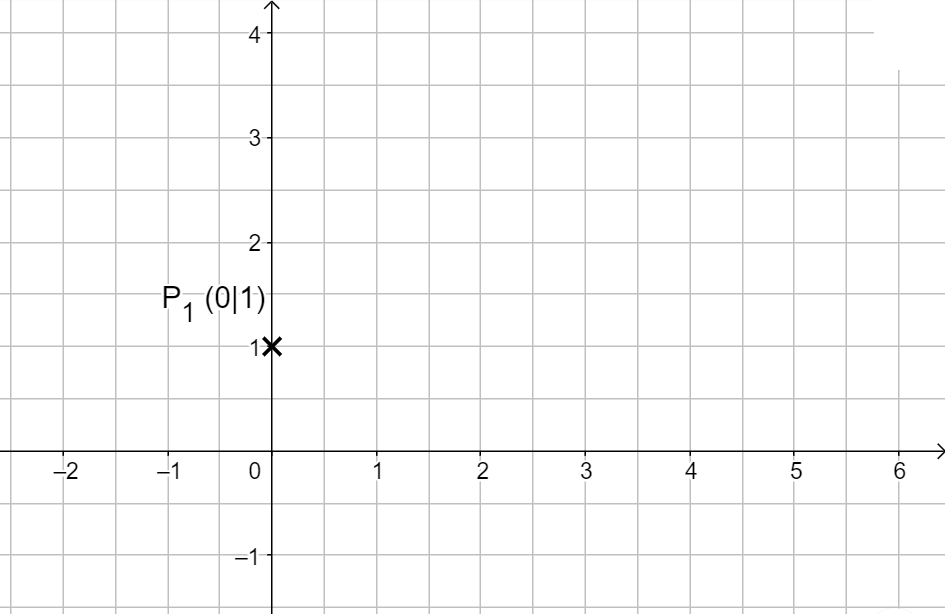
Erster Wert \(x = 0\):
Eingabe in den Taschenrechner:
\( \frac{1}{3} \cdot 0 + 1 = 1 \Rightarrow \, x = 0 ; \, y = 1 \, \Rightarrow P_1 (0|1)\)
Wiederhole für einen zweiten Punkt für x, um einen zweiten Punkt zu bekommen und verbinde sie zu einer Geraden.
Zweiter Wert \(x = 1\): Eingabe in den Taschenrechner: \( \frac{1}{3} \cdot 1 + 1 = 1,333…\)
Und hier ist auch schon das Problem mit dieser Methode: Es kann sein, dass der berechnete y-Wert nicht exakt eingezeichnet werden kann, dann musst du von vorne anfangen.
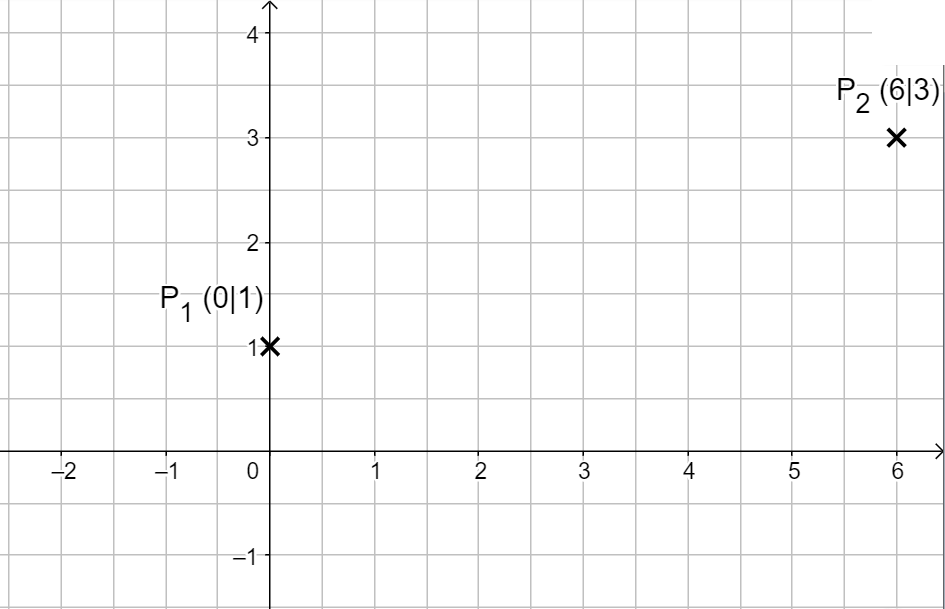
Neuer zweiter Wert: \(x = 6;\)
Eingabe in den Taschenrechner:
\( \frac{1}{3} \cdot 6 + 1 = 3 \Rightarrow \, x = 6 ; \, y = 3 \, \Rightarrow P_2 (6|3)\)
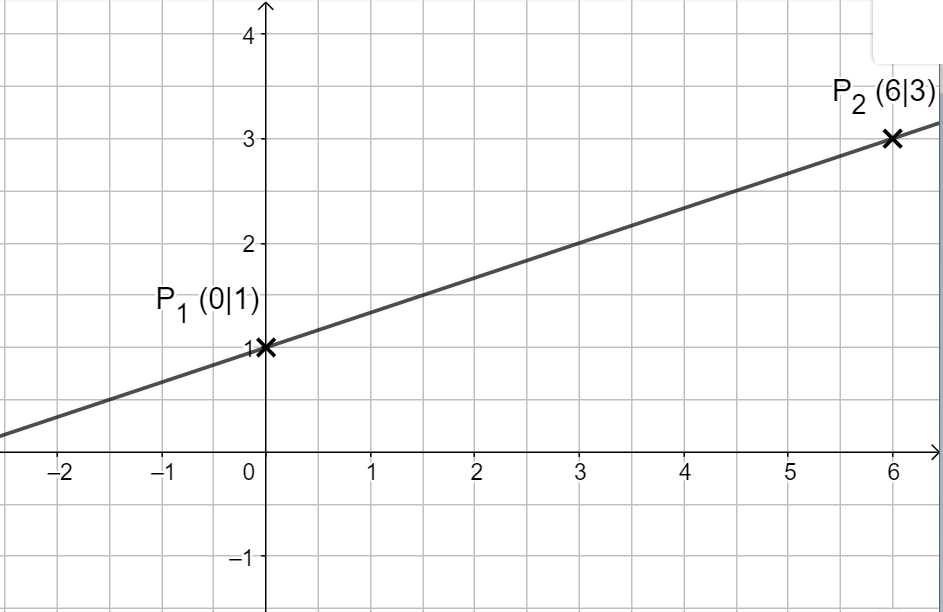
Dann noch beide Punkte verbinden und du bist fertig.
Suche dir die Methode aus, die dir am besten gefällt und lege gleich los!
Übungsaufgaben: Geraden zeichnen
Wie sollte es beim MAP-Hack auch sonst sein, geübt wird an Abschlussprüfungsaufgaben.
