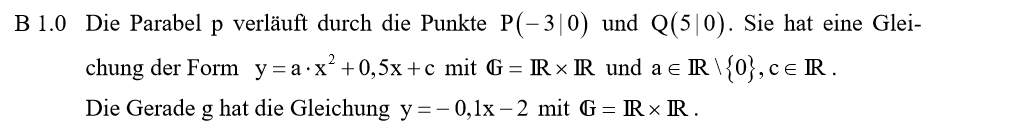

Lösungen zu B1.1
Es sind zwei Punkte P und Q gegeben. Du verstendest also das Vorgehen „Parabel aus zwei Punkten bestimmen“. Die Koordinaten werden ins Gleichungssystem eingesetzt und nachdem du es umgeformt hast, kannst du es mit dem GTR lösen.
\begin{align} (I) y &= ax^2 + 0,5x + c \\ &(II) y = ax^2 + 0,5x + c \\ \\ &P(-3|0) \in (I) \\ &Q(5|0) \in (II) \\ \\ (I) 0 &= a \cdot (-3)^2 + 0,5 \cdot (-3) + c \\ &(II) 0 = a \cdot 5^2 + 0,5 \cdot 5 + c \\ \\ (I)0 &= 9a -1,5 + c \, \, \, | +1,5 \\ &(II) = 25a + 2,5 + c \, \, \, |-2,5 \\ \\ \Rightarrow >R: \, a = -0,25 \, ; \, c = 3,75 \\ \Rightarrow &y = -0,25x^2 + 0,5x + 3,75 \end{align}
Zurück zum MAP-Hack:

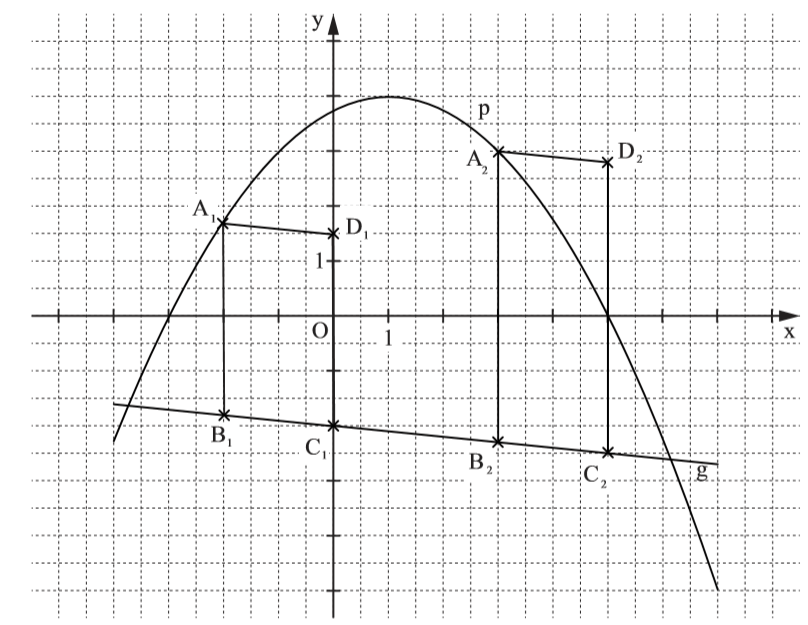
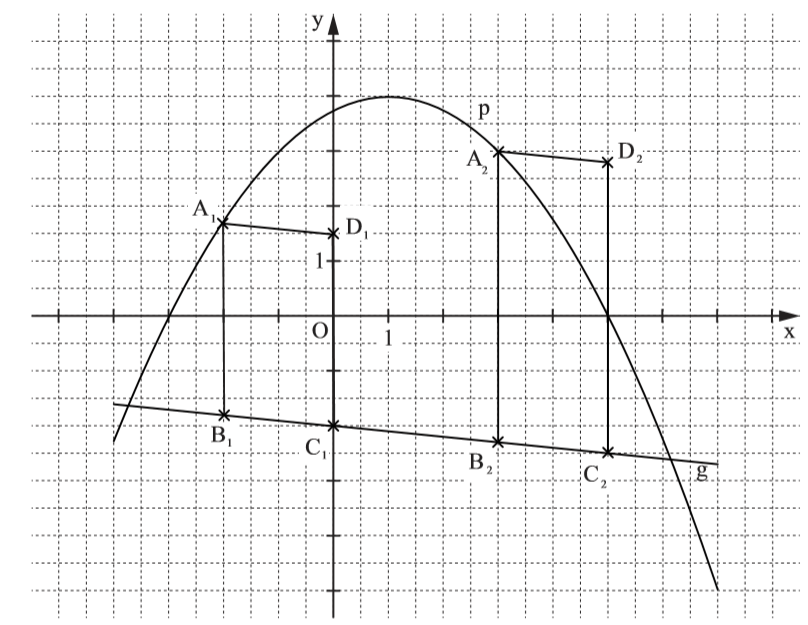
Lösung zu B1.2
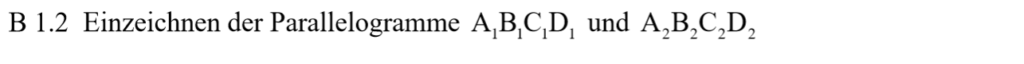
Zurück zum MAP-Hack:
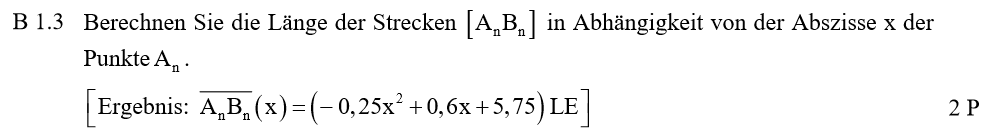
Lösungen zu B1.3
Weil A und B dieselbe Abszisse x haben, kannst du die Länge der Strecke [AB] mit „oben – unten“ berechnen.
\begin{align} &\overline{A_n B_n} \, mit \, oben \, – \, unten: \\
\overline{A_n B_n} &= y_A – y_B \\
&= -0,25x^2 + 0,5x + 3,75 – (-0,1x – 2) \\
&= -0,25x^2 + 0,5x + 3,75 + 0,1x +2 \\ \Rightarrow &\overline{A_n B_n} = (-0,25x^2 + 0,6x + 5,75) LE \end{align}
Zurück zum MAP-Hack:

Lösungen zu B1.4
Zuerst musst du den funktionalen Flächeninhalt des Parallelogramms bestimmen. Hier geht das besonders einfach mit der Formel \( A = g \cdot h \), denn wenn du dein Blatt um 90° dreht, dann kannst du [AB] als Grundseite und 2 als Höhe verwenden. h = 2 funktioniert, weil die Abszisse x von D und C immer um 2 größer ist als die von A und B.
\begin{align} A_{Parallelogramm} &= g \cdot h \\&= (-0,25x^2 + 0,6x + 5,75) \cdot 2 \\ \Rightarrow A_{Parallelogramm} &= (-0,5x^2 + 1,2x + 11,5) FE \\ \\ &Aufstellen \, der \, Gleichung: \\ A_{Parallelogramm} &= 13 \\ -0,5x^2 + 1,2x + 11,5 &= 13 \,\,\, |-13 \\ -0,5x^2 +1,2x – 1,5 &= 0 \\ \Rightarrow >R: Keine \, Lösung! \end{align}
Weil die Gleichung keine Lösung hat, gibt es auch kein Parallelogramm mit dem Flächeninhalt von 13 FE.
Zurück zum MAP-Hack:
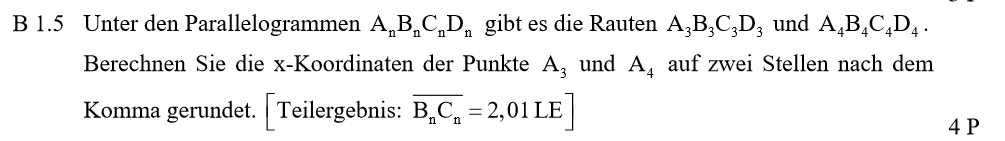
Lösungen zu B1.5
Eine Raute hat die besondere Eigenschaft, dass jeweils zwei nebeneinanderliegende Seiten gleich lang sind. Hier findest du den Ansatz für die Gleichung. Du berechnest [BC] aus den Koordinaten des Vektors und setzt für die Länge von [AB] die Formel von oben ein.
\begin{align} &\overline{B_n C_n} \, aus \, den \, Vektorkoordinaten: \\
\overline{B_n C_n} &= \sqrt{2^2 + (-0,2)^2} = 2,01 LE \\
\\
&Ansatz \, aus \, den \, Rauteneigenschaften \\
\overline{A_n B_n} &= \overline{B_n C_n} \\
-0,25x^2 + 0,6x + 5,75 &= 2,01 \, \, \, |-2,01 \\
-0,25x^2 + 0,6x – 3,74 &= 0 \\
\Rightarrow >R: x = -2,85 \, \lor \, x = 5,25 \end{align}
Zurück zum MAP-Hack:
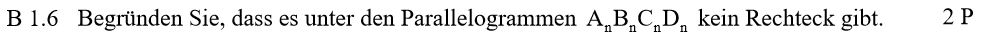
Lösungen zu B1.6
Dass ein Parallelogramm gleichzeitig ein Rechteck ist, müssen die Winkel alle 90° sein. Die Gerade AB ist parallel zur y-Achse. Dass die anderen Seite damit einen rechten Winkel einschließt, muss die Steigung also 0 sein. Die Steigung der Gerade BC ist aber nie 0 und damit gibt es keinen rechten Winkel und auch kein Rechteckt.

Warum ist bei der ersten aufgabe eine 5
Leider weiß ich nicht, welche 5 du meinst. Der Punkt Q hat die x-Koordinate 5 und die wird für jedes x in der Gleichung eingesetzt, falls du diese meinst.
Frage gerne nochmal!