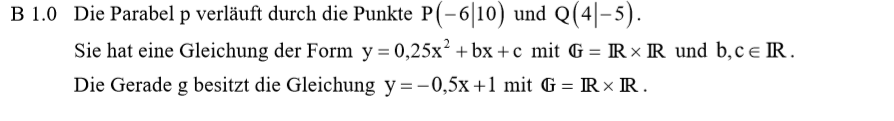

Lösung zu B1.1
Es sind zwei Punkte P und Q gegeben. Du verstendest also das Vorgehen „Parabel aus zwei Punkten bestimmen“. Die Koordinaten werden ins Gleichungssystem eingesetzt und nachdem du es umgeformt hast, kannst du es mit dem GTR lösen.
\begin{align}(I) y &= 0,25x^2 + b \cdot x + c \\
&(II) y = 0,25x^2 + b \cdot x + c \\
\\
&P(-6|10) \in p \, \in (I) \, ; \, Q(4|-5) \in p \, in (II) \\
\\
(I) 10 &= 0,25 \cdot (-6)^2 + b \cdot (-6) + c \\
&(II) -5 = 0,25 \cdot 4^2 + b \cdot 4 + c \\
\\
(I) 10 & = 9 – 6b + c \, \, \,|-9 \\
&(II) -5 = 4 + 4b + c \,\,\ |-4 \\
\\
(I) 1 &= -6b +c \\
&(II) -9 = 4b + c \\
\\
\Rightarrow >R: b= -1 ; c = -5 \\
\\
&\Rightarrow y = 0,25x^2 -x – 5 \end{align}
Zurück zum MAP-Hack:

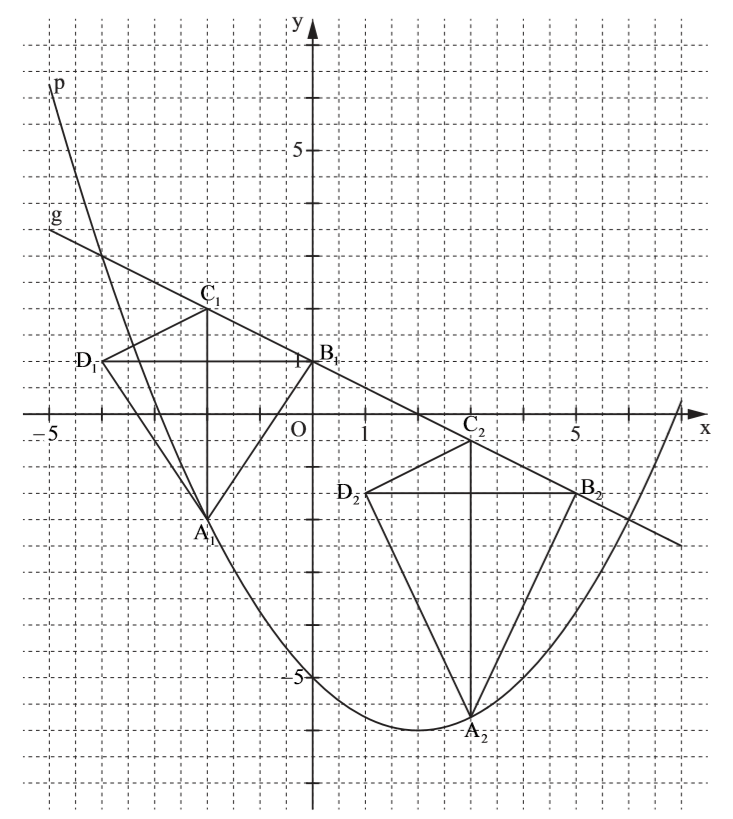
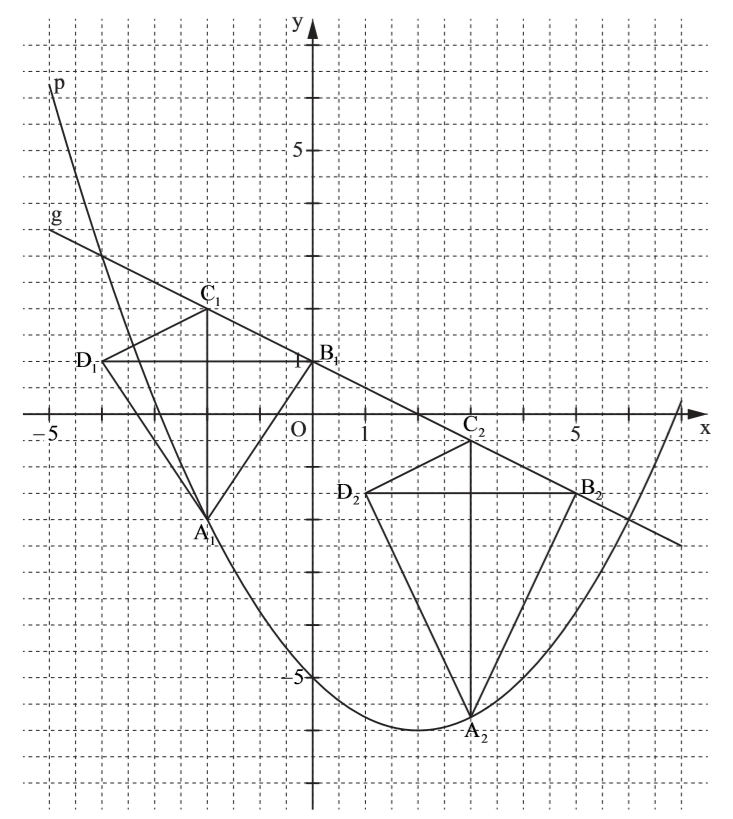
Lösung zu B1.2
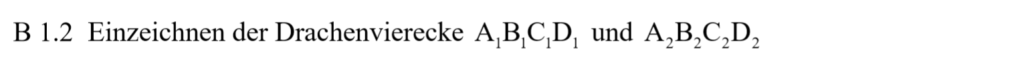
Zurück zum MAP-Hack:
Lösung zu B1.3
Der Punkt D liegt zwei LE weiter links als die Punkte A bzw C. Also gilt für \(x_D = x – 2 \). D liegt außerdem auf der selben Höhe wie B. Also gilt \( y_D = y_B = -0,5(x+2)+1 \). Der Punkt \( D_n(x|y)\) ergibt sich zu \(D_n(x-2 | -0,5(x+2)+1)\) oder \(D_n(x-2 |-0,5x)\)

Lösung zu B1.4
Um den Flächeninhalt der Raute (\( A_{Raute} = 0,5 \cdot e \cdot f \)) zu bestimmen, benötigst du die Länge der Diagonale \(\overline{A_n C_n} \). Weil A und C die selbe Abszisse haben, kannst du mit „oben – unten“ ansetzen.
\begin{align} &\overline{A_n C_n} \, durch \, „oben \, – \, unten“: \\ \overline{A_n C_n} &= y_{Gerade} – y_{Parabel} \\ &= -0,5x + 1 – (0,25x^2 -x – 5) \\ &= -0,25x^2 + 0,5x + 6 \\ \\ &Einsetzen \, in \, die \, Flächenformeln: \\ A_{Raute} &= 0,5 \cdot \overline{A_n C_n} \cdot \overline{BD} \\ &= 0,5 \cdot (-0,25x^2 + 0,5x + 6) \cdot 4 \\ \Rightarrow &A(x) = -0,5x^2 + x + 12 FE \end{align}
Zurück zum MAP-Hack:

Lösung zu B1.5
Bestimme mit dem GTR und der Formeln \( \overline{A_n C_n} = -0,25x^2 + 0,5x + 6 \) den Extremwert: \(\overline{A_0 C_0} = 6,25 LE \) für \(\). Setzte den Wert für x bei B ein:
\begin{align} B_0 (x +2 |-0,5(x+2) +1) &= B_0 (1+2 |-0,5 (1+2) +1) \\ \Rightarrow &B_0 =(3| -0,5) \end{align}
Lösung zu B1.6
Stelle anhand der Vorgabe zur Streckenlänge von [BD] eine Gleichung auf und löse sie.
\begin{align} \overline{A_n C_n} &= 1,5 \cdot \overline{B_n D_n} \\ -0,25x^2 +0,5x +6 &= 1,5 \cdot 4 \, \, \, | -(1,5\cdot 4) \\ -0,25x^2 + 0,5x + 6 – 1,5 \cdot 4 &= 0 \\ -0,25x^2 + 0,5x &= 0 \\ \Rightarrow >R: x = 0 \, \lor \, x = 2 \end{align}
Zurück zum MAP-Hack:
Lösung zu B1.7
Der Winkel ist immer gleich, da B und D eine Gerade bilden, die parallel zur x-Achse ist. Damit ist der Winkel CBD ein Wechselwinkel zu dem Winkel, den die Gerade mit der x-Achse einschließt. Weil dieser Winkel immer gleich ist – die Gerade ändert sich ja nicht – ändert sich auch der Winkel CBD nicht.
Das gehört nicht mehr zur Aufgabe, aber mit dem Tangens könnte man auch ganz schnell diesen Winkel bestimmen:
\begin{align} tan(\alpha) &= m = -0,5 \\ \alpha &= tan^{-1} (-0,5) = 26,56° \end{align}

Hallo!
Ich hätte bei 1.7 so begründet: |BD| läuft immer parallel zur x-Achse, Punkt Bn liegt auf der Gerade wie Cn und sie haben immer den selben Abstand zu einander.
Denkt ihr ich bekomme dafür den Punkt?
Hm das kommt am Ende stark auf deinen Korrektor an. Gaaaanz streng genommen fehlt, dass C und B auf einer Geraden liegen, denn sie könnten ja trotz gleichen Abstandes merkwürfige Dinge tun. Aber es steckt schon sehr viel Richtiges in deiner Antwort.
Du hast eine Frage zu einer Teilaufgabe oder zur Lösung? Schreib‘ hier und du bekommst eine Antwort!