

Lösung zu B1.1
Es sind zwei Punkte P und Q gegeben. Du verstendest also das Vorgehen „Parabel aus zwei Punkten bestimmen“. Die Koordinaten werden ins Gleichungssystem eingesetzt und nachdem du es umgeformt hast, kannst du es mit dem GTR lösen.
\begin{align} (I) y &= 0,4x^2 + bx + c \\ &(II) y = 0,4x^2 + bx + c \\ \\ P&(-9|44) \, in \, (I) \\ &Q(6|14) \, in \, (II) \\ \\ (I) y &= 0,4 \cdot (-9)^2 + b \cdot (-9) + c \\ &(II) y = 0,4 \cdot 6^2 + b \cdot 6 + c \\ \\ (I) 44 &= 32,4 – 9 b + c \, \, \, |-32,4 \\ &(II) 14 = 14,4 + 6b + c \,\,\, |-14,4 \\ \\ (I) 11,6 &= -9b + c \\ &(II) -0,4 = 6b + c \\ \\ \Rightarrow >R \, b = -0.8 \, \land \, c = 4,4 \end{align}

Zurück zum MAP-Hack:

Lösung zu B1.2
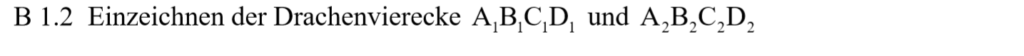
Zurück zum MAP-Hack:
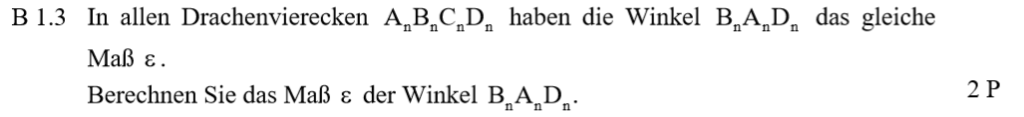
Lösung zu B1.3
\begin{align} &\varepsilon \, aus \, den \, Vektorkoordinaten: \\ tan(\frac{\varepsilon}{2}) &= \frac{2}{3} \\ \Rightarrow &\varepsilon = 67,38° \end{align}

Lösung zu B1.4
Um in die Flächenformel des Drachen (\(A_{Drache} = 0,5 \cdot e \cdot f \)) einsetzen zu können, benötigst du die Länge der Strecke [AC]. A und C haben die selbe Abszisse, also kannst du die Strecken durch „oben – unten“ berechnen:
\begin{align}&\overline{A_n C_n} \, durch \, oben \, – \, unten: \\
\overline{A_n C_n} &= y_{Parabel} – y_{Gerade} \\
&= 0,4x^2 – 0,8x + 4,4 – (0,2x + 0,5) \\
&= 0,4x^2 – 0,8x + 4,4 – 0,2x – 0,5 \\
&= 0,4x^2 -x + 3,9 \\ \\ &A_{Drache} \, mit \, der \, Flächenformel: \\
A_{Drache} &= 0,5 \cdot \overline{A_n C_n} \cdot \overline{B_n D_n} \\
&= 0,5 \cdot (0,4x^2 – x + 3,9) \cdot 4 \\
&= 2 \cdot (0,4x^2 – x + 3,9) \\
\Rightarrow &A_{Drache} = (0,8x^2 – 2x + 7,8) FE \\
\\ &Berechnung \, des \, Extremwerts: \\ GTR: &A_{min} = 6,55 FE \, für x = 1,25 \end{align}
Zurück zum MAP-Hack:
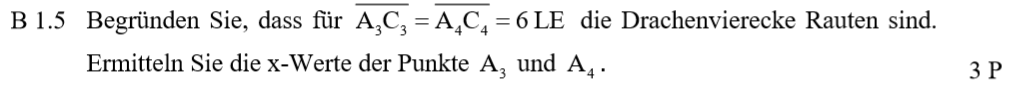
Lösung zu B1.5
Ein Drachenviereck wird zur Raute, wenn sich die Diagonalen halbieren. Weil die y-Werte von B und C immer um 3 größer sind, also die y-Werte von A, müssen die y-Werte von C um 6 größer sein, als die y-Werte von A. Damit lässt sich ein Ansatz für eine Gleichung finden:
\begin{align} \overline{A_n C_n} &= 6 \\ 0,4x^2 – x + 3,9 &= 6 \,\,\, |-6 \\ 0,4x^2 -x – 2,1 &= 0 \\ \Rightarrow GTR \, x = -1,36 \, &\lor \, x = 3,86 \end{align}
Zurück zum MAP-Hack:
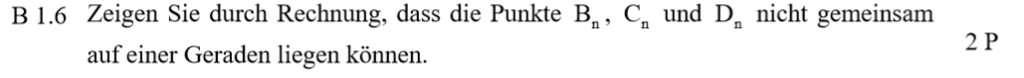
Lösung zu B1.6
Wenn die Punkte auf einer Gerade liegen, dann muss die Länge der Strecke [AC] 3 LE sein. Damit lässt sich der Ansatz für eine Gleichung finden.
\begin{align} \overline{AC} &= 3 \\ 0,4x^2 – x + 3,9 &= 3 \,\,\, | – 3 \\ 0,4x^2 – x + 0,9 &= 0 \\ \Rightarrow GTR: \, Keine \, Lösung \end{align}
Weil die Gleichung keine Lösung besitzt, können die Punkte auch nicht auf einer Geraden liegen.
