2.0 Die nebenstehende Skizze zeigt en Axialschnitt eines massiven Eierbechers aus Holz. MS ist die Symmetrieachse.
Es gilt:
\( |\overline{AB}|= 9,0 cm; \, |\overline{CD}|= 4,0 cm; \\ \angle BAD = 52° ; r = |\overline{EC}| \)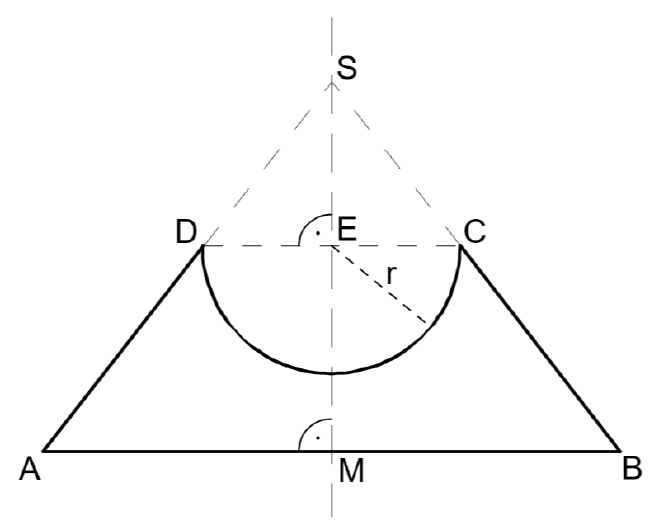
Runden Sie auf eine Stelle nach dem Komma.
2.1 Berechnen Sie die Längen der Strecken \(|\overline{MS}| \text{ und } |\overline{ES}| \).
[Ergebnis: \( |\overline{MS}| = 5,8 cm ; |\overline{ES}| = 2,6 cm \) ]
Lösung zu 2.1
\begin{align} |\overline{MS}| \text{ mit dem Tangens:}\\
tan(\angle MAS) &= \frac{|\overline{MS}|}{|\overline{AM}|} \,\,\, |\cdot |\overline{AM}| \\
|\overline{MS}| &= tan(\angle MAS) \cdot |\overline{AM}| \\
&= tan(52°) \cdot 4,5 \\
&\Rightarrow |\overline{MS}| = 5,8 \text{cm} \\
\\
&|\overline{ES}| \text{ mit dem Vierstreckensatz:}\\
\frac{|\overline{ES}|}{|\overline{MS}|} &= \frac{|\overline{DC}|}{|\overline{AB}|}\\
\frac{|\overline{ES}|}{5,8} &= \frac{4}{9} \,\,\, |\cdot 5,8 \\
&\Rightarrow |\overline{ES}| = \frac{4}{9} \cdot 5,8 = 2,6 \text{cm} \end{align}
2.2 Bestimmen Sie das Volumen V des Eierbechers.
Lösung zu 2.2
Das gesuchte Volumen entsteht, wenn man vom Kegel (ABS im Schrägbild) den Kegel (DCS) und die Halbkugel abzieht.
Weil du alle benötigten Streckenlängen kennst, kannst du direkt in die Formeln einsetzen:
\begin{align}
V_{ABS} &= \frac{1}{3} \cdot \pi \cdot |\overline{AM}|^2 \cdot |\overline{MS}| \\
&= \frac{1}{3} \cdot \pi \cdot 4,5^2 \cdot 5,8 \\
&\Rightarrow V_{ABS} = 123,0 \text{cm}^3 \\
\\
V_{DCS} &= \frac{1}{3} \cdot \pi \cdot |\overline{DE}|^2 \cdot |\overline{ES}| \\
&= \frac{1}{3} \cdot \pi \cdot 2^2 \cdot 2,6 \\
&\Rightarrow V_{DCS} = 10,9 \text{cm}^3 \\
\\
V_{Halbkugel} &= \frac{1}{2} \cdot \frac{4}{3} \cdot \pi \cdot |\overline{ED}|^3 \\
&= \frac{1}{2} \cdot \frac{4}{3} \cdot \pi \cdot 2^3 \\
&\Rightarrow V_{Halbkugel} = 16,8 \text{cm}^3 \\
\\
V_{ges} &= V_{ABS} – V_{DCS} – V_{Halbkugel} \\
&= 123,0 – 10,9 – 16,8 \\
&\Rightarrow V_{ges} = 95,3 \text{cm}^3 \end{align}
2.3 Der Innenbereich und der Boden soll in blauer Farbe gestaltet werden. Bestimmen Sie die geplante blaue Oberfläche.
Lösung zu 2.3
Die gesuchte Oberfläche setzt sich aus dem „Boden“, also einem Kreis und der Oberfläche der Halbkugel zusammen. Diese kannst du einzeln berechnen und dann addieren.
\begin{align}
O_{Boden} &= \pi \cdot |\overline{AM}|^2 \\
&= \pi \cdot 4,5^2 \\
&\Rightarrow O_{Boden} = 63,6 \text{cm}^2 \\
\\
O_{Halbkugel} &= 0,5 \cdot 4 \cdot \pi \cdot |\overline{ED}|^2 \\
&= 0,5 \cdot 4 \cdot \pi \cdot 2^2 \\
&\Rightarrow O_{Halbkugel} = 25,1 \text{cm}^2 \\
\\
O_{ges} &= O_{Boden} + O_{Halbkugel} \\
&= 63,6 + 25,1 \\
&\Rightarrow O_{ges} = 88,7 \text{cm}^2 \end{align}
