Die nebenstehende Skizze zeigt ein Schrägbild des geraden Prismas ABCDEFGH, deren Grundfläche eine Raute ABCD mit Mittelpunkt ist. Die Punkte E, F, G und H liegen jeweils senkrecht über der Punkten A, B, C und D und bilden Rauten EFGH mit Mittelpunkt S .
Es gilt:
\( |\overline{AM}| = 6 cm; |\overline{BD}|= 9 cm ; |\overline{AE}| = 6 cm \)
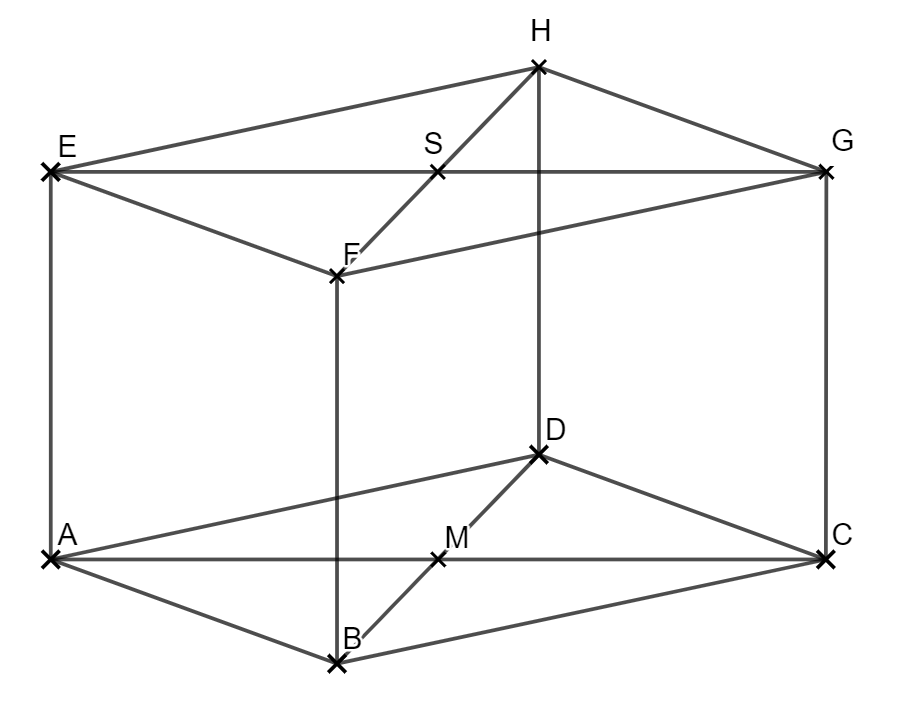
Runden Sie im Folgenden auf zwei Stellen nach dem Komma.
2.1 Zeichnen Sie das Schrägbild des Prismas ABCDEFGH, wobei die Strecke \( \overline{AC}\) auf der Schrägbildachse und der Punkte A links vom Punkt C liegen soll.
Für die Zeichnung gilt: q = 0,5 ; ω = 45°.
Lösung zu 2.1
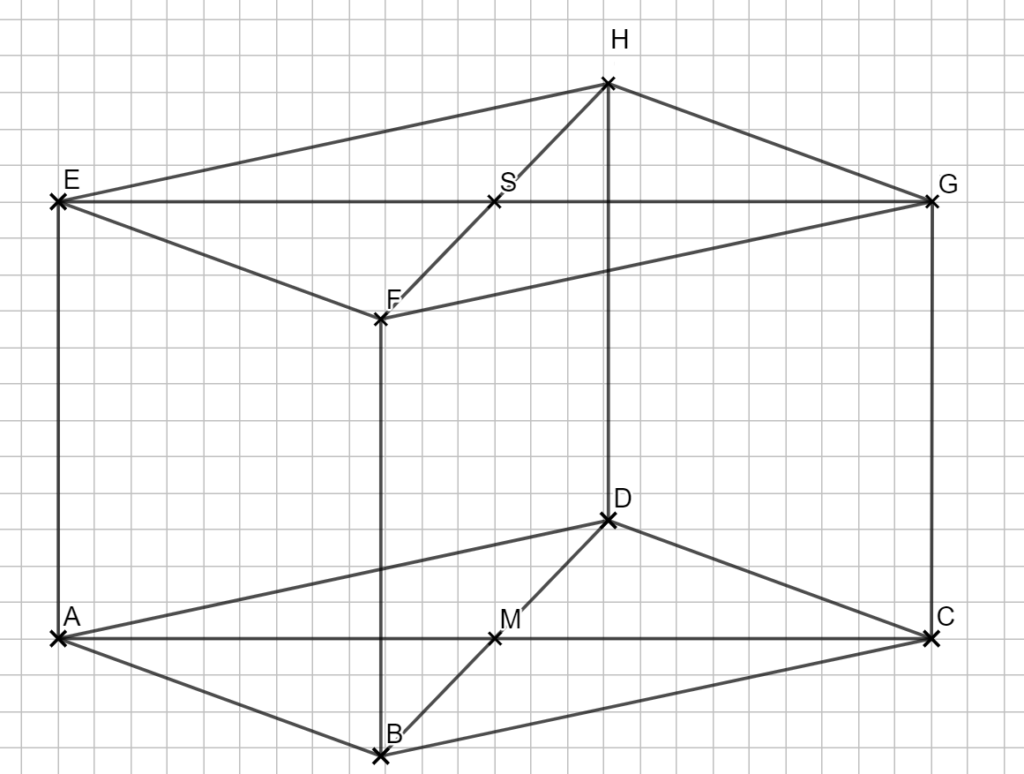
2.2 Zeigen Sie rechnerisch, dass für die Länge der Strecke \( \overline{AB} \) gilt: \( |\overline{AB}| = 7,5 cm \).
Lösung zu 2.2
\begin{align}
&|\overline{AB}| \text{ mit dem Satz des Pythagoras:}\\
|\overline{AB}|^2 &= |\overline{AM}|^2 + |\overline{BM}|^2 \\
&= 6^2 + 4,5^2 \,\,\, |\sqrt{}\\
&\Rightarrow |\overline{AB}| = 7,5 cm \end{align}
2.3 Verlängert man die Höhe \( \overline{MS} \) über S hinaus um x cm, so erhält man Punkte Sn. Verkürzt man gleichzeitig die Diagonale \( \overline{AC} \) der Grundfläche von der Punkten A und C aus um jeweils 0,5x cm, so erhält man Punkte An und Cn mit x aus ]0 ; 12 [ und x ∈ ℝ.
Die Punkte An, B, Cn und D sind Eckpunkte der Grundflächen von Pyramiden AnBCnDSn mit den Spitzen Sn.
Zeichnen Sie die Pyramide A1BC1DS1 für x = 2 ins das Schrägbild zu 1.1 ein.
Lösung zu 2.3
Einzeichnen der Pyramide
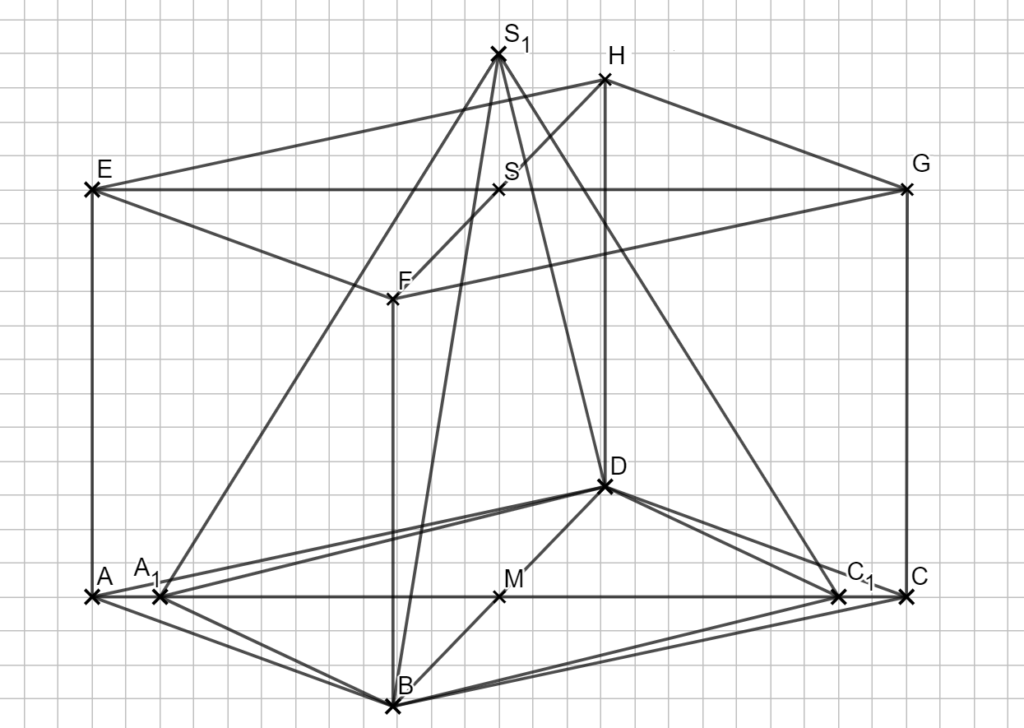
2.4 Zeigen Sie, dass sich das Volumen V der Pyramiden AnBCnDSn in Abhängigkeit von x gilt:
V(x) = (-1,5x² + 9x + 108) cm³.
Lösung zu 2.4
Für die Höhe der Pyramide gilt:\(|\overline{MS_n}| = 6 + x\), weil \(|\overline{MS}| = 6\) um x verlängert wird.
Die Diagonale \(|\overline{BD}| = 9\) hat eine feste Länge.
Die andere Diagonale wird von beiden Seiten um 0,5x verkürzt, insgesamt also um \(2 \cdot 0,5x = 1x\). Es gilt: \(|\overline{A_n S_n}| = 12 – x\)
\begin{align} &\text{Einsetzen in die Flächenformel:}\\
V(x) &= \frac{1}{3} \cdot A_G \cdot h \\
&= \frac{1}{3} \cdot \frac{1}{2} \cdot |\overline{A_n C_n}| \cdot |\overline{BD}| \cdot |\overline{M S_n}| \\
&= \frac{1}{3} \cdot \frac{1}{2} \cdot (12 – x) \cdot 9 \cdot (6 + x)\\
&= 1,5 \cdot (12 – x) \cdot (6 + x) \\
&= (18 – 1,5x) \cdot (6 + x) \\
&= 108 + 18x – 9x – 1,5x^2 \\
&\Rightarrow V(x) = -1,5x^2 + 9x + 108 \end{align}
2.5 Bestimmen Sie die Werte für x, für das Volumen der Pyramide A3BC3DS3 gleich 50% des Volumens des Prismas ABCDEFGH ist.
Lösung zu 2.5
Zuerst musst du das Volumen des Primsa bestimmen, um dann eine GLeichung mit dem prozentualen Anteil aufzustellen.
\begin{align} &V_{ABCDEFG} \text{ über die Flächenformel:}\\
V_{ABCDEFG} &= A_G \cdot h \\
&= \frac{1}{2} \cdot |\overline{AC}| \cdot |\overline{BD}| \cdot |\overline{MS}| \\
&= \frac{1}{2} \cdot 12 \cdot 9 \cdot 6 \\
\Rightarrow V_{ABCDEFG} = 324 \text{cm}^3 \\
\\
&x \text{über den prozentualen Anteil:}\\
V(x) &= 0,5 \cdot V_{ABCDEFG} \\
-1,5x^2 + 9x + 108 &= 0,5 \cdot 324 \\
-1,5x^2 + 9x + 108 &= 162 \,\,\, |-162 \\
-1,5x^2 +9x -54 &= 0 \\
&\Rightarrow \text{ Taschenrechner: Error} \end{align}
Es gibt keine Pyramide, die das halbe Volumen des Primas hat.
2.6 Bestimmen Sie das Intervall für x, für das gilt:
\( \angle BA_nM > \angle MBA_n \)
Lösung zu 2.6
Im Dreieck liegt der größere Winkel der größeren Seite gegenüber. Je länger \( |\overline{MA_n}|\) ist, desto kleiner ist also \( \angle MA_nB \) und je größer \( |\overline{MA_n}|\) desto größer \( \angle MBA_n \)
Die einfachere Frage zur Beantwortung der Aufgabe ist also „Wann gilt \( |\overline{MB}| > |\overline{MA_n}| \)„. Damit lässt sich eine Gleichung aufstellen.
\begin{align} |\overline{MB}| &> |\overline{MA_n}| \\
4,5 &> 6 – 0,5x \,\,\, |-6\\
-1,5 &> -0,5 \,\,\, |:(-0,5) \text{ \, Inversionsgesetz!}\\
3 &< x \end{align}
Das gesuchte Intervall ist \( x \in \) ]3;12[
