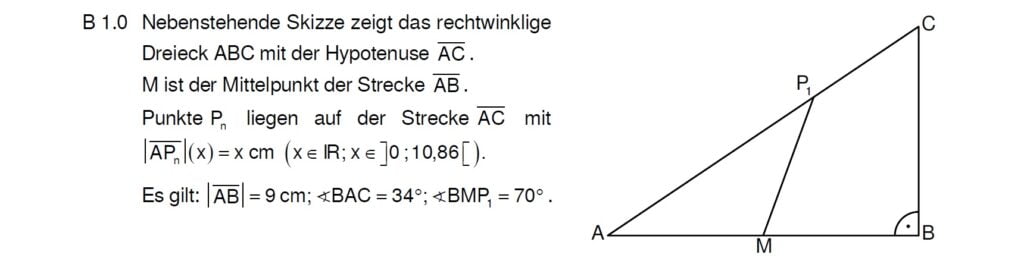

Lösung zu B1.1
Suche dir Dreiecke, in denen du drei Angaben hast und berechne.
\begin{align} & |\overline{AC}| \, mit \, dem \, Cosinus: \\
cos(\angle BAC) &= \frac{|\overline{AB}|}{|\overline{AC}|} \, \, \, | \cdot |\overline{AC}| : cos(\angle BAC) \\
|\overline{AC}| &= \frac{|\overline{AB}|}{cos(\angle BAC)} = \frac{9}{cos(34°)} \\
\Rightarrow |\overline{AC}| &= 10,86 cm \end{align}
Weil im Dreieck \( AMP_1 \) nur eine Streckenlänge gegeben ist, muss du mit dem Sinus-Satz arbeiten. Dazu benötigst du die beiden fehlenden Winkel im Dreieck.
\begin{align} \angle P_1 MA &= 180° – \angle BMP_1 = 180° – 70° \\
&= 110° \\
\angle AP_1 M &= 180° – \angle BAC – \angle P_1 MA = 180° – 34° – 110° \\
&= 36° \\ \\ &\overline{AP_1} \, mit \, dem \, Sinus-Satz: \\
\frac{|\overline{AP_1}|}{sin(\angle P_1 MA)} &= \frac{|\overline{AM}|}{sin(\angle AP_1 M)} \\
\frac{|\overline{AP_1}|}{sin(110°)} &= \frac{0,5 \cdot 9}{sin(36°)} \, \, \, |\, \cdot sin(110°) \\ |\overline{AP_1}| &= \frac{4,5 \cdot sin(110°)}{sin(36°)} =7,19 cm\end{align}

Lösung zu B1.2
Minimale Strecken deuten auf die Rechtwinkligkeit beim Abstand hin. Aber wo ist der rechte Winkel?
Am Punkt \( P_0 \) ist im Dreieck \(\triangle AMP_0 \) ein rechter Winkel. In diesem Dreieck kennst du 3 Angaben und kann die Streckenlänge direkt bestimmen.
\begin{align} &|\overline{MP_0}| \text{ mit dem Sinus:}\\
sin(\angle BAC) &= \frac{|\overline{MP_0}|}{|\overline{AM}|} \\
sin(34°) &= \frac{|\overline{MP_0}|}{4,5}\,\,\, |\cdot 4,5 \\
\Rightarrow &|\overline{MP_0}| = sin(34°) \cdot 4,5 = 2,52 cm \end{align}
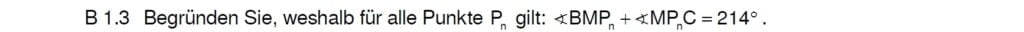
Lösung zu B1.3
Die Innenwinkelsumme im Viereck führt zum Ziel.
Die gesuchten Winkel \(\angle BMP_n \) und \(\angle MP_N C \) sind beide im Viereck BCPM. Du bestimmt zuerst den Winkel ACB, um dann mit der Innenwinkelsumme im Viereck anzusetzen.
\begin{align} &\angle ACB \, mit \, der \, Innenwinkelsumme \, im \, Dreieck \\
180° &= \angle ABC + + \angle ACB + \angle CBA \\
\angle ACB &= 180° – 90° – 34° = 56° \\
\\
&Ansatz \, über \, die \, Innenwinkelsumme \, im \, Viereck: \\
360° &= \angle BMP_n + \angle MP_n C + \angle CBA + \angle ACB \\
360° &= \angle BMP_n + \angle MP_n C + 56° + 90° | – 56° -90° \\
214° &= \angle BMP_n + \angle MP_n C \end{align}

Schlaues Kerlchen
Ja, sie steht im Intervall. Das ist häufiger mal so, den Trick kann man sich merken.
Hallo, ich hätte eine Frage zur Aufgabe B 1.2.
In der Aufgabe soll man die Strecke MP0 ausrechnen.
In der Lösung steht ja, dass man im Dreieck AMP0 mit dem Tangens (34 Grad) rechnet. Ich dachte man benutzt da Sinus,also von dem Winkel BAC, die Gegenkathete (MP0) geteilt durch die Hypothenuse (AM).
Deswegen kommt bei mir als Ergebnis 2,52 cm raus.
Stimmt das?
Ja stimmt, habe es ausgebessert. Danke!
Bei B 1.1 ist doch der rechte Winkel bei <APM und somit "sin Alpha = MP/AM"
MP = sin34°*4,5cm = 2,52cm.
Hallo Valentin,
leider ist bei APM kein rechter Winkel. Das kannst du dir z.B. daran überlegen, dass der Winkel „auf der anderen Seite“ 70° sind. Das kann ja nicht sein, weil sie zusammen 180° sein müssen.
Frage gerne wieder!