Was passiert, wenn Mathe-Lehrer morgens gedankenversunken in Kaffee kochen? Es kommt eine Aufgabe dabei heraus. Ja, genau so ist diese Aufgabe entstanden. Sie ist – zugegeben – etwas schwieriger als das, was man von dir in der Prüfung erwartet, aber was soll es. Viel Spaß beim Üben!
Die Kaffeefilterkanne von Stelton hat einen Standfußdurchmesser von 11 cm und kann bis zum schmalen Punkt unter dem Ausguss gefüllt werden.
a) Berechnen Sie die Füllmenge der Kanne. Entnehmen Sie notwendige Größen dem Bild.

Die Kanne ist ein Kegelstumpf und um ihr Volumen zu bestimmen, kannst du die Zeichnung gedanklich zum Kegel ergänzen. Das aber nur zum Verständnis was hier passiert, denn die Gesamthöhe des Kegels kennen wir nicht.
Zur Berechnung des Kegelstumpfes benötigst du das Volumen des großen Kegels und das Volumen des kleinen Kegels. Aus der Zeichnung kannst du folgende Größen abschätzen:
Durchmesser an der schmalen Stelle: d = 6 cm
Höhe bis zur schmalen Stelle: h = 14 cm
Winkel zwischen Mantel und Grundfläche: 80°
(Aus der Angabe) Durchmesser des Grundkreises: D = 11 cm
Mit diesem Infos kannst du die Gesamthöhe H des Kegels berechnen.
\begin{align} tan(80°) &= \frac{H}{5,5} \,\,\, |\cdot 5,5 \\
\Rightarrow &H = 31,19 = 31cm \end{align}
Damit hast du alles zusammen, um die einzelnen Volumina zu berechnen:
\begin{align} V_{klein} &= \frac{1}{3} \cdot \pi \cdot r^2 \cdot (H – h) \\
&= \frac{1}{3} \cdot \pi \cdot 3^2 \cdot (31 – 14) \\
\Rightarrow & V_{klein} = 160,22 cm^3 \\
\\
V_{groß} &= \frac{1}{3} \cdot \pi \cdot R^2 \cdot H \\
&= \frac{1}{3} \cdot \pi \cdot 5,5^2 \cdot 31 \\
\Rightarrow V_{groß} = 982,01 cm^3 \\
\\
V_{Kanne} &= V_{groß}- V_{klein}\\
&= 982,01 – 160,22 \\
\Rightarrow &V_{Kanne}= 821,79 cm^3 \end{align}
Das sind 0,82 dm³ also ungefähr 0,8 liter. Das wahre Volumen (laut Amazon) sind 0,6 liter. Dass das wahre Volumen kleiner ist ergibt Sinn, da wir immer mit den Außenmaßen rechnen, die Wand der Kanne auch eine Dicke besitzt.
Wenn dich diese Aufgabe nicht abgeschreckt hat, dann kannst du mit dem zweiten Teil weitermachen.
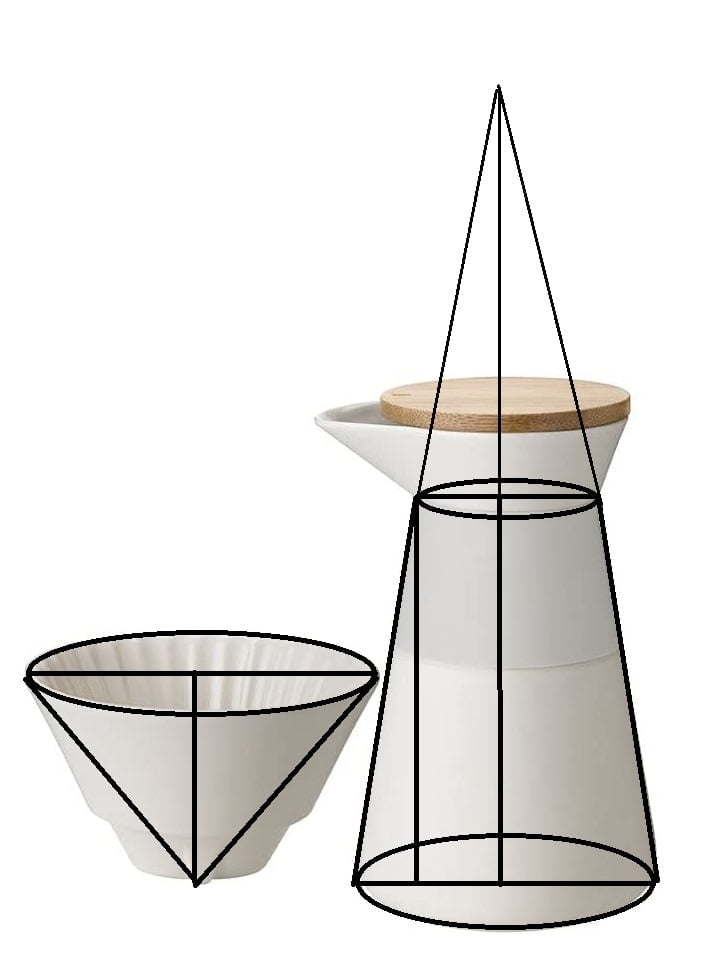
b) Wie häufig muss der Kaffeefilter gefüllt werden, bis die Kanne voll ist? Modellieren Sie den Filter als Kegel.
Zuerst musst du wieder die notwendigen Größen anhand der Zeichnung schätzen:
Der Durchmesser ist etwas gleich, also 11 cm.
Die Höhe ist ungefähr 8 cm.
\begin{align} V_{filter} & = \frac{1}{3} \cdot \pi \cdot 5,5^2 \cdot 8 \\
\Rightarrow &V_{filter} = 252,42 cm^3 \end{align}
Jetzt einfach das Volumen der Kanne durch das Volumen des Filters teilen, dass du weißt „wie häufig der Filter in die Kanne passt“.
\begin{align} V_{Kanne} : V_{Filter} = 821,79 : 252,42 = 3,25 \end{align}
Der Filter muss ungefähr 3 mal gefüllt werden. Dass man in Wirklichkeit weniger Wasser braucht ergibt auch Sinn, schließlich muss in den Filter noch Kaffeepulver.
Aus reichlicher praktischer Erfahrung kann ich bestätigen, dass 3 mal den Filter füllen die Kanne füllt.

