2.0 Der Wert eines zwei Jahre alten Gebrauchtwagens beträgt derzeit 12750 €. Bei gleichbleibendem prozentualen Wertverlust lässt sich nach x Jahren der Zeitwert y € des Wagens durch die Funktion f mit der Gleichung \( y = 12750 \cdot 0,84^x \) mit G = ℝ 0+ x ℝ 0+ beschreiben.
2.1 Ergänzen Sie die Wertetabelle auf Ganze gerundet.
Zeichnen Sie sodann den Graphen zu f in das Koordinatensystem ein.
| x | 0 | 2 | 4 | 6 | 8 | 10 |
| y |
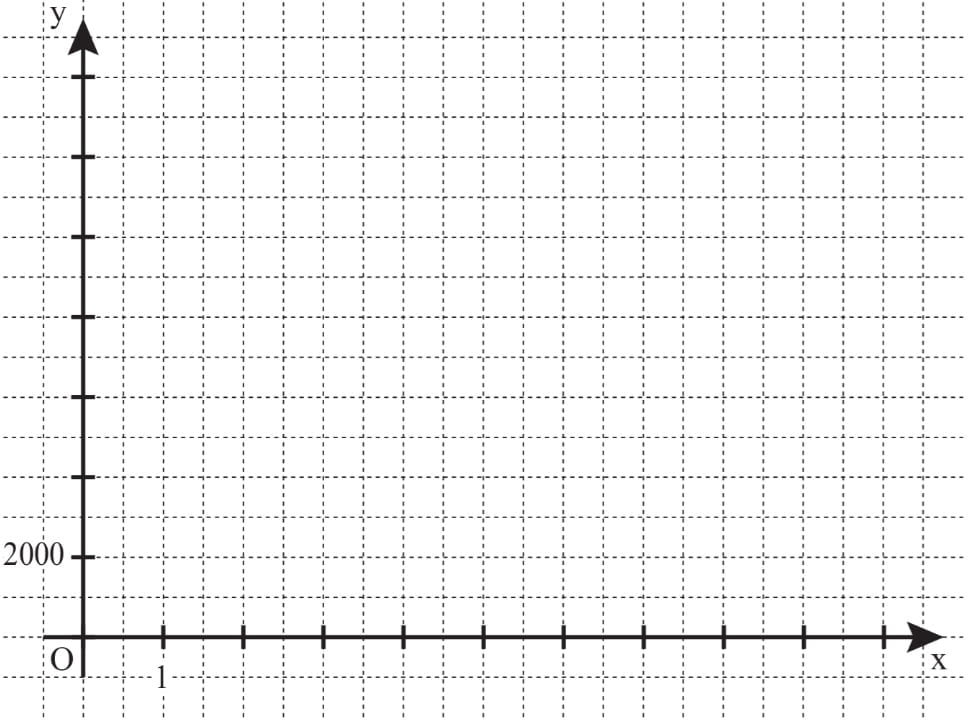
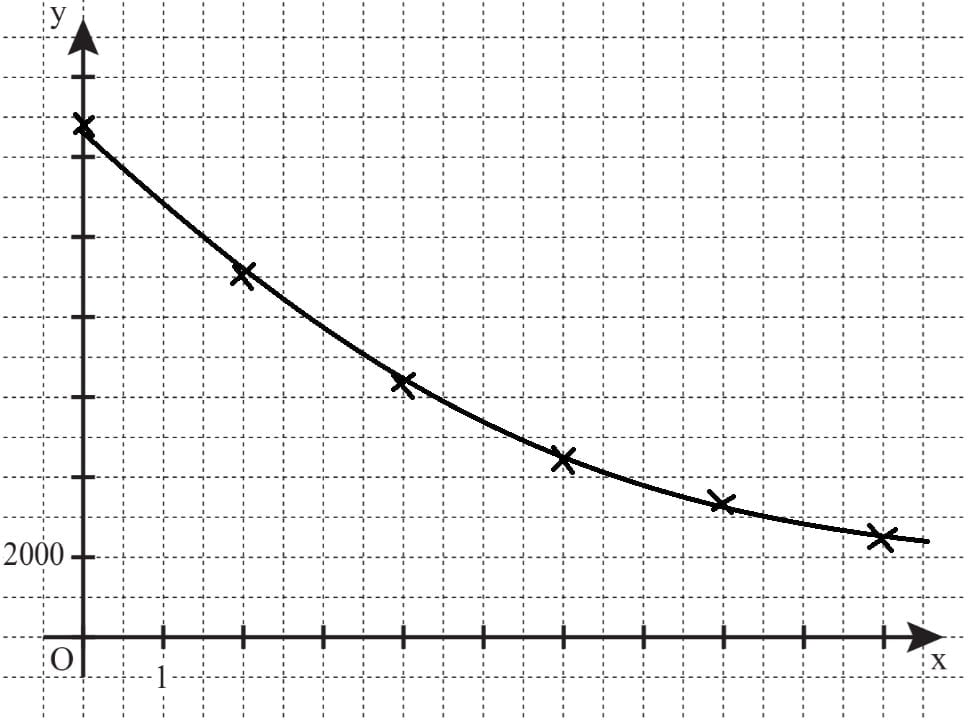
Lösung zu 2.1
| x | 0 | 2 | 4 | 6 | 8 | 10 |
| y | 12750 | 8996 | 6348 | 4479 | 3160 | 2230 |
2.2 Welcher prozentuale jährliche Verlust wird angenommen?
Es sind ____ %.
Lösung zu 2.2
0,84 sind 0,16 weniger als 1. Das sind \( 0,16 \cdot 100 \% = 16 \% \)
2.3 Kosten für Autos können über sogenannte Abschreibungen über einen Zeitraum von 6 Jahren steuerlich geltend machen. Berechnen Sie den Restwert des Autos nach Ablauf der Abschreibung, wenn der PKW als Neuwagen angeschafft wurde.
Lösung zu 2.3
Von den 6 Jahren Abschreibung sind bereits 2 Jahre vergangen. Gesucht ist also \( f(4) \).
\( f(4) = 12750 \cdot 0,84^4 = 6348 \) €
2.4 Das Auto soll mit einem Zeitwert von 5000 € verkauft werden. Berechnen Sie, wie lange man mit dem Verkauf des Wagens warten muss.
Lösung zu 2.4
\begin{align} f(x) &= 5000 \\
12750 \cdot 0,84^x &= 5000= \,\,\, |:12750 \\
0,84^x &= 0,39 \,\,\, |log_{0,84} \\
x &= 5,4 \text{Jahre} \end{align}
