Lösung zu A2.1
Das Dreieck hat keinen rechten Winkel, also darfst du nur Cosinus-Satz oder Sinus-Satz verwenden. Du hast aber keinen Winkel gegeben!
\begin{align} &\angle BAC \text{ mit dem umgeformten Cosinussatz:}\\
cos(\angle BAC) &= \frac{|\overline{AB}|^2 +|\overline{AC}|^2 – |\overline{BC}|^2}{2 \cdot |\overline{AB}| \cdot |\overline{AC}|}\\
&= \frac{4^2 + 12^2 – 10^2}{2 \cdot 4 \cdot 12}\,\,\, |cos^{-1} \\
\Rightarrow &\angle BAC = 51,32° \end{align}
Hier geht es zur allgemeinen Erklärung:
Lösung zu A2.2
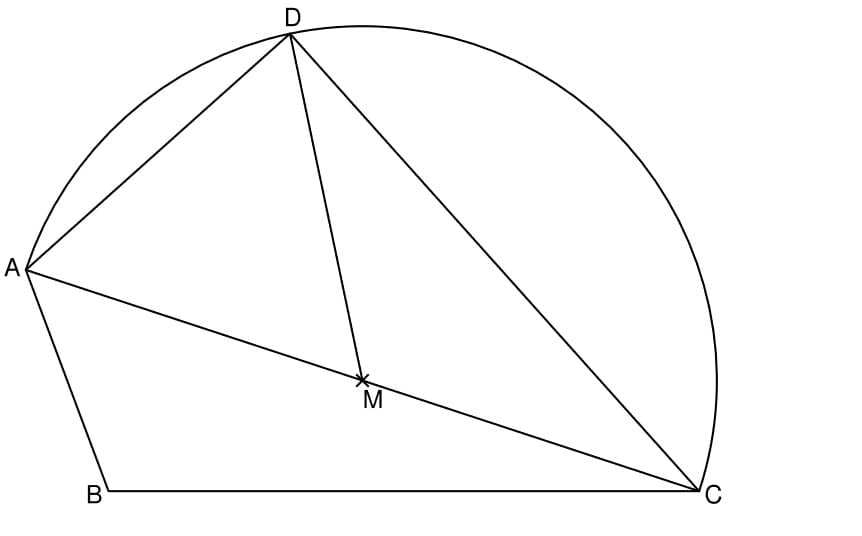
Genau lesen! Von welcher Strecke ist es der Mittelpunkt? Bis wohin geht die Kreislinie?
Hier geht es zur allgemeinen Erklärung:
Lösung zu A2.3
Ein Kreis über einer Strecke ist die Vorraussetzung für den Satz des Thales. Was besagt der Satz des Thales?
Der Winkel ADC hat das Maß 90°, weil der Punkt D auf dem Thaleskreis über die Strecke \( \overline{AC} \) liegt.
Das Dreieck AMD ist gleichseitig, da \( |\overline{AM}| = |\overline{DM}| = |\overline{AD}| = 6 cm \)
Hier geht es zur allgemeinen Erklärung:
Lösung zu A2.4
Achtung genau lesen! Die gesuchte Figur setzt sich aus dem Kreissektor und den Dreiecken ABC bzw. CDM zusammen. Hier bietet es sich an, die Flächeninhalte der Dreiecke mit der Sinusformel zu berechnen, weil man jeweils einen eingeschlossenen Winkel kennt.
\begin{align} &\text{Berechnung der Teilflächen:}\\
A_{Sektor} &= \frac{\angle DMA}{360°} \cdot |\overline{AM}|^2 \cdot \pi \\
&= \frac{60°}{360°} \cdot 6^2 \cdot \pi \\
&= 18,85 cm^2 \\
\\
A_{ABC} &= 0,5 \cdot |\overline{AB}| \cdot |\overline{AC}| \cdot sin(\angle BAC)\\
&= 0,5 \cdot 4 \cdot 12 \cdot sin(51,32°)\\
&= 18,74 cm^2 \\
\\
A_{CDM} &= 0,5 \cdot |\overline{CM}| \cdot |\overline{DM}| \cdot sin(\angle CMD) \\
&= 0,5 \cdot 6 \cdot 6 \cdot sin(120°) \\
&= 15,59 cm^2 \\
\\
&\text{Addieren zur Gesamfläche:}\\
A &= 18,85 + 18,74 + 15,59 = 53,18 cm^2 \end{align}