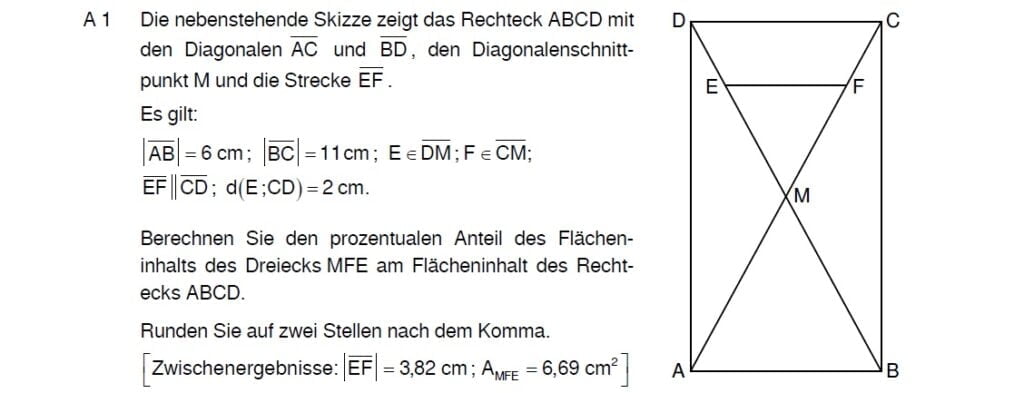
Lösungen zu 1
Berechne zuerst die Ersatzergebnisse, sie sind der Weg zum Ziel.
d(E; CD) bedeuted, dass der Abstand von D zur Gerade CD 2 cm ist, also wenn man von E senkrecht nach oben geht. Es ist nicht die Streckenlänge DE!
\begin{align} &\text{Flächeninhalt des Vierecks }A_{ABCD} \\
A_{ABCD} &= l \cdot b \\
&= |\overline{AB}| \cdot |\overline{BC}|\\
&= 6 \cdot 11 \\
\Rightarrow &A_{ABCD} = 66 \text{cm}^2 \end{align}
Für den Flächeninhalt des Dreiecks \( MFE \) benötigst du den Abstand von M zu EF und die Länge der Strecke \( \overline{EF} \)
Wir berechnen diese beiden Streckenlängen, um dann auf den Flächeninhalt zu schließen.
\begin{align} &d(M;EF) \text{ durch Subtraktion} \\
d(M;EF) &= 0,5 \cdot |\overline{BC}| – d(E;CD) \\
&= 0,5 \cdot 11 – 2 \\
\Rightarrow &d(M;EF) = 3,5 \text{cm}\\
\\
&\overline{EF} \text{ mit dem Vierstreckensatz:}\\
\frac{|\overline{EF}|}{|\overline{AB}|} &= \frac{d(M;EF)}{0,5 \cdot |\overline{BC}|} \\
\frac{|\overline{EF}|}{6} &= \frac{3,5}{5,5} \,\,\, |\cdot 6 \\
|\overline{EF}| &= \frac{3,5}{5,5} \cdot 6 \\
\Rightarrow &|\overline{EF}| = 3,82 \text{cm}\\
\\
&\text{Flächeninhalt des Dreiecks } MFE \\
A_{MFE} &= 0,5 \cdot g \cdot h \\
&= 0,5 \cdot |\overline{EF}|\cdot d(M;EF) \\
&= 0,5 \cdot 3,82 \cdot 3,5 \\
\Rightarrow &A_{MFE} = 6,69 \text{cm}^2 \\
\\
&\text{Prozentsatz } p \text{ mit der Prozentformel:}\\
p &= \frac{\text{Anteil}}{\text{Ganze}} \cdot 100 \% \\
&= \frac{6,69}{66}\cdot 100\% \\
\Rightarrow &p = 10,14 \% \end{align}
