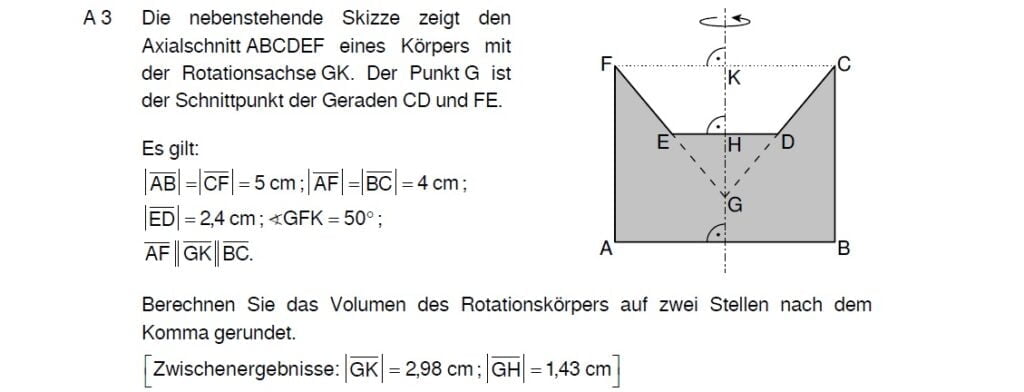
Lösungen zu A3
Berechne zuerst die Zwischenergebnisse.
Der Rotationskörper ist ein Zylinder, aus dem ein Kegelstumpf ausgeschnitten ist. Berechne die Teilvolumina und addiere/subtrahiere dann.
\begin{align} &\text{Ansatz zur Lösung:}\\
V &= V_{Zylinder} – V_{Kegelstumpf}\\
\\
&V_{Zylinder} \text{ über die Volumenformel:}\\
V_{Zylinder} &= |\overline{FK}|^2 \cdot \pi \cdot |\overline{AF}| \\
&= 2,5^2 \cdot \pi \cdot 4 \\
&\Rightarrow V_{Zylinder} = 78,54 cm^3 \\
\\
&|\overline{GK}| \text{ mit dem Tangens:}\\
tan(\angle GFK) &= \frac{|\overline{GK}|}{|\overline{FK}|} \\
tan(50°) &= \frac{|\overline{GK}|}{2,5} \,\,\, |\cdot 2,5\\
&\Rightarrow |\overline{GK}| = 2,98 cm \\
\\
&V_{Kegel} \text{ mit der Kegelformel:}\\
V_{Kegel} &= \frac{1}{3} |\overline{FK}|^2 \cdot \pi \cdot |\overline{GK}|\\
&=\frac{1}{3} \cdot 2,5^2 \cdot \pi \cdot 2,98 \\
&\Rightarrow V_{Kegel} = 19,50 cm^3 \\
\\
&|\overline{GH}| \text{ über den Tangens:}\\
tan(\angle GEH) &= \frac{|\overline{GH}|}{|\overline{EH}|} \\
tan(50°) &= \frac{|\overline{GH}|}{1,2} \,\,\, |\cdot 1,2\\
&\Rightarrow |\overline{GH}| = 1,43 cm\\
\\
&V_{Kleiner Kegel} \text{ mit der Kegelformel:}\\
V_{KK} &= \frac{1}{3} \cdot |\overline{EH}|^2 \cdot \pi \cdot |\overline{GH}| \\
&= \frac{1}{3} \cdot 1,2^2 \cdot \pi \cdot 1,43 \\
&\Rightarrow V_{KK} = 2,16cm^3 \\
\\
V_{Kegelstumpf} &= V_{Kegel} – V_{KK} \\
&= 19,50cm^3 – 2,16cm^3 \\
&\Rightarrow V_{Kegelstumpf} = 17,34 cm^3 \\
\\
&\text{Einsetzen in den Ansatz:}\\
V &= V_{Zylinder} – V_{Kegelstumpf}\\
&= 78,54 – 17,34 \\
&\Rightarrow V = 61,20 cm^3 \end{align}

Gleich nachdem du 20 Melonen gekauft und jede in 12,5 gleiche Stücke geschnitten hast 😉
Hallo,
Woher weiß man welcher Körper voneinander abgezogen werden soll.
Hallo Lena,
naja, am Ende muss der graue Kröper rauskommen und da musst du dir überlegen, ob du die Körper addierst oder subtrahierst. Addieren musst du, wenn man die Körper „zusammenklebt“. Wenn man Körper „doppelt zählt“ oder ausschneidet, dann subtrahiert man.
Hoffentlich hilft dir das =)