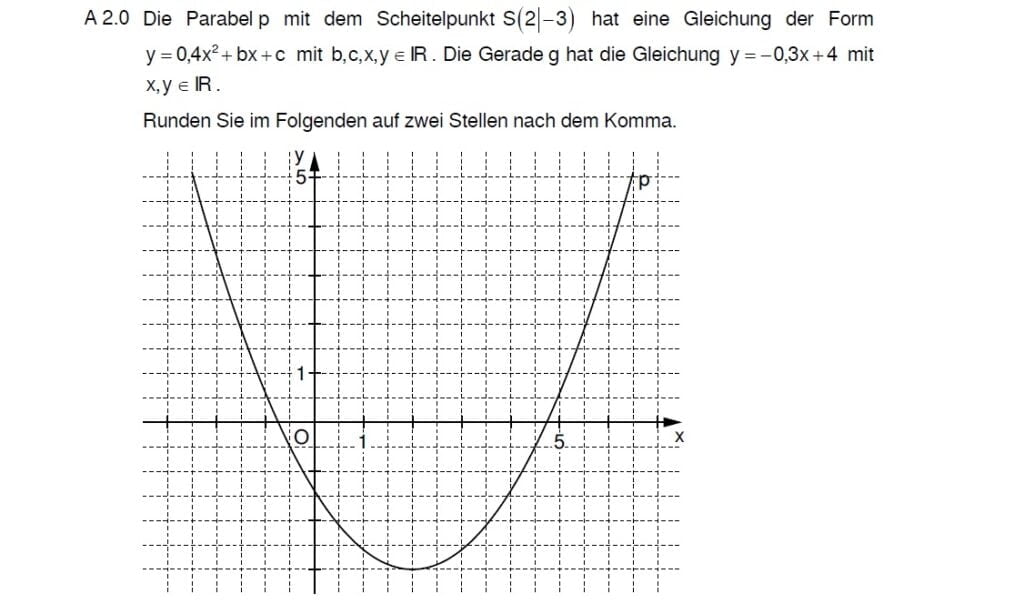

Lösung zu 2.1
Du hast den Scheitelpunkt geben. Brauchst du den Ansatz mit einem Gleichungssystem oder mit der Scheitelform?
Die Gerade zeichnest du mit deinem Grundwissen. Grundwissen nicht gefunden? Hier nachlesen: https://map-hack.de/grundwissen/geraden-einzeichnen/
Der Scheitelpunkt S(2|-3) ist gegeben, also wählst du den Ansatz mit dem der Scheitelformel:
\begin{align} y &= a \cdot (x – x_s) ^2 + y_s \\ \\ & mit \, a = 0,4 \\ &S(2|-3) \Rightarrow x_s = 2 \, ; \, y_s = -3 \\ \\ y &= 0,4 \cdot (x – 2)^2 – 3 \\ &= 0,4 \cdot (x^2 -4x + 4) – 3 \\ &= 0,4x^2 -1,6x +1,6 – 3 \\ \Rightarrow &y = 0,4x^2 – 1,6x – 1,4 \end{align}
Zurück zum MAP-Hack:

Lösung zu 2.2
Aufgabe von hinten lesen! Erstmal bei x = 2 starten und dann Schritt für Schritt!

SIehe Video 😉
Zurück zum MAP-Hack:

Lösung zu 2.3
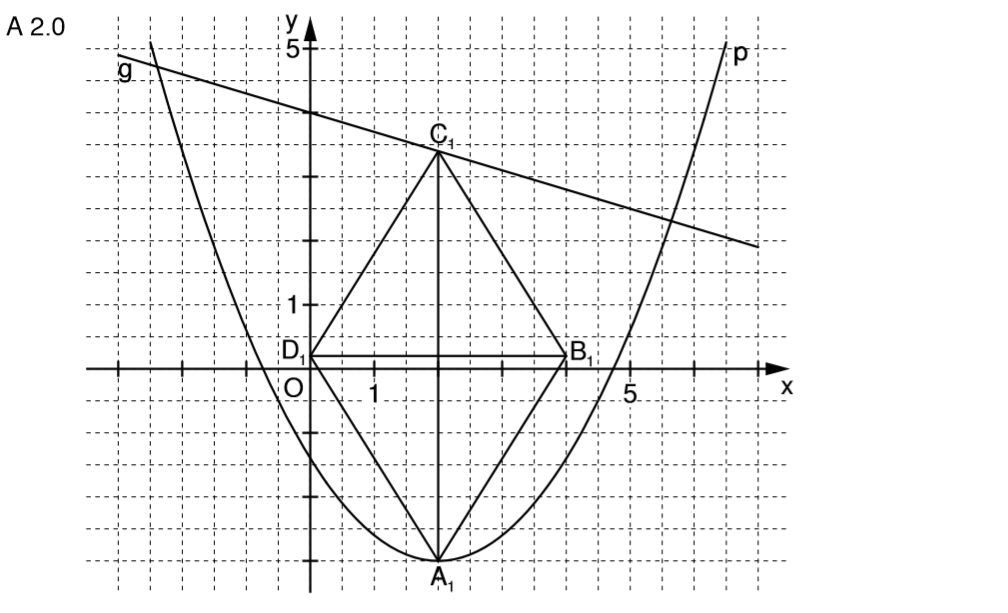
Zuerst musst du den funktionalen Flächeninhalt aufstellen. Dazu „oben – unten“ und diesen term in den Flächeninhalt der Raute einsetzen und vereinfachen. Diese Formel mit 15 gleichsetzen und die Gleichung lösen. Ja, es ist viel zu tun!
Um den Flächeninhalt der Raute zu bestimmen, musst du die Länge der Diagonalen AC und BD bestimmen. Aus der Angabe weißt du, dass BD immer die Länge 4 hat. Die Punkte A und C haben die selben Abszisse, also kannst du den Ansatz „oben – unten“ wählen:
\begin{align} &Berechnung \, von \, |\overline{AC}|: \\
|\overline{AC}| &= y_{Gerade} – y_{Parabel} \\
&= -0,3x + 4 – (0,4x^2 – 1,6x – 1,4) \\
&= -0,4x^2 + 1,3x + 5,4 \\
\\
&Berechnung \, des \, Flächeninhalts: \\
A_{Raute} &= 0,5 \cdot |\overline{AC}| \cdot |\overline{BD}| \\
&= 0,5 \cdot (-0,4x^2 + 1,3x + 5,4) \cdot 4 \\
\Rightarrow &A_{Raute} = (-0,8x^2 + 2,6x +10,8) FE \\
\\
&Berechnung \, des \, Extremwerts \, mit \, dem \, GTR: \\
\Rightarrow &A_{max} = 12,91 FE \end{align}
Weil der größte mögliche Flächeninhalt 12,91 FE kleiner als 15 FE ist, kann es keine Raute mit 15 FE geben.
Zurück zum MAP-Hack:

Lösung zu 2.4
Das Quadrat hat die besondere Eigenschaft, dass die Diagonalen gleich lang sind. Über diese Eigenschaft kannst du eine Gleichung aufstellen und die quadratische Gleichung mit dem GTR lösen.
\begin{align} |\overline{AC}| &= |\overline{BD}| \\
-0,4x^2 + 1,3x + 5,4 & = 4 \, \, \, |-4 \\ -0,4x^2 +1,3x +1,4 &= 0 \\
&Löse \, mit \, dem \, GTR \\
\Rightarrow &x_1 = -0,85 \lor x_2 = 4,1 \end{align}
Die Diagonale \(\overline{BD}\) ist 4 LE lang, also ist die x-Koordinate von B um 2 größer als die von A und C. Um auf die x-Koordinate von B zu schließen, addierst du einfach 2.
\( x_{B_1} = -0,85 + 2 = 1,15 \, ; \, x_{B_2} = 4,1 + 2 = 6,1 \)
Warum sind es die Koordinaten von A und C, wenn man die beiden Werte gleichsetzt?
Weil A und C die Schnittpunkte der Funktionen sind. Hier sind die beiden Funktionen gleich. Deshalb „ist gleich =“
Ist die Angabe „x ∈ [ -3 ; 7 ]“ nicht relevant für die Aufgabe 2.1?
Im Prinzip ja, aber em Ende steht ja einfach da „Zeichne die Parabeln in das vorliegende Koordinatensystem sein“, denn das KoSy geht ja von -3 bis 7. Es wird auch nie eine AUfgabe geben, die lautet „Zeichne die Parabel ein, aber nur in einem eingeschränkten Bereich“, denn das würde ja keinen Sinn ergeben.
Hallo,
wie berechnet man bei der 2.4 die Koordinaten von B?
Weil es eine Quadrat sein soll, kannst du den Diagonalenlängen gleichsetzen und damit ein x ausrechnen.
Schau in den Lösungen mal das Erklärvideo an, da habe ich es recht ausführlich erklärt.
Viel Erfolg nächste Woche!
Du hast eine Frage zu einer Teilaufgabe oder zur Lösung? Schreib’ hier und du bekommst eine Antwort!