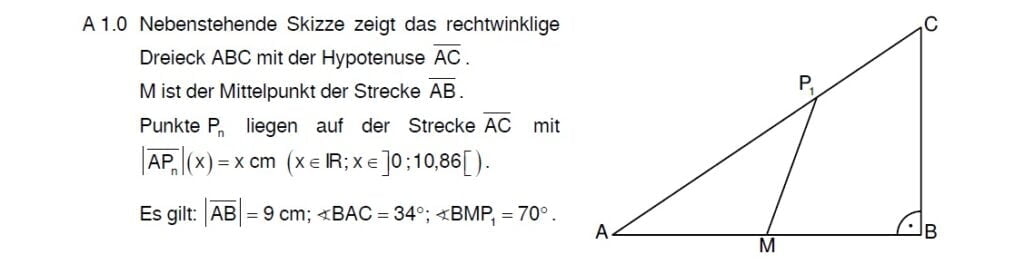

Lösung zu 1.1
Suche dir Dreiecke, in denen zu drei Angaben hast. Falls dieser Plan nicht funktioniert, musst du mit einem Hilfsdreieck arbeiten.
\begin{align} & |\overline{AC}| \, mit \, dem \, Cosinus: \\
cos(\angle BAC) &= \frac{|\overline{AB}|}{|\overline{AC}|} \, \, \, | \cdot |\overline{AC}| : cos(\angle BAC) \\
|\overline{AC}| &= \frac{|\overline{AB}|}{cos(\angle BAC)} = \frac{9}{cos(34°)} \\
\Rightarrow |\overline{AC}| &= 10,86 cm \end{align}
Weil im Dreieck \( AMP_1 \) nur eine Streckenlänge gegeben ist, muss du mit dem Sinus-Satz arbeiten. Dazu benötigst du die beiden fehlenden Winkel im Dreieck.
\begin{align} \angle P_1 MA &= 180° – \angle BMP_1 = 180° – 70° \\
&= 110° \\ \angle AP_1 M &= 180° – \angle BAC – \angle P_1 MA = 180° – 34° – 110° \\ &= 36° \\
\\
&\overline{AP_1} \, mit \, dem \, Sinus-Satz: \\
\frac{|\overline{AP_1}|}{sin(\angle P_1 MA)} &= \frac{|\overline{AM}|}{sin(\angle AP_1 M)} \\
\frac{|\overline{AP_1}|}{sin(110°)} &= \frac{0,5 \cdot 9}{sin(36°)} \, \, \, |\, \cdot sin(110°) \\
|\overline{AP_1}| &= \frac{4,5 \cdot sin(110°)}{sin(36°)} =7,19 cm\end{align}
Zurück zum MAP-Hack:
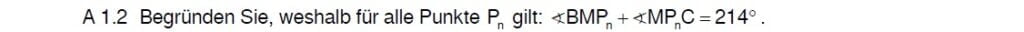
Lösung zu 1.2
Ein Dreieck hat eine Innenwinkelsumme von 180°. Im Viereck ist sie auch immer gleich.
Die gesuchten Winkel \(\angle BMP_n \) und \(\angle MP_N C \) sind beide im Viereck BCPM. Du bestimmt zuerst den Winkel ACB, um dann mit der Innenwinkelsumme im Viereck anzusetzen.
\begin{align} &\angle ACB \, mit \, der \, Innenwinkelsumme \, im \, Dreieck \\
180° &= \angle ABC + \angle ACB + \angle CBA \\
\angle ACB &= 180° – 90° – 34° = 56° \\
\\ &Ansatz \, über \, die \, Innenwinkelsumme \, im \, Viereck: \\
360° &= \angle BMP_n + \angle MP_n C + \angle CBA + \angle ACB \\
360° &= \angle BMP_n + \angle MP_n C + 56° + 90° | – 56° -90° \\ 214° &= \angle BMP_n + \angle MP_n C \end{align}

Du hast eine Frage zu einer Teilaufgabe oder zur Lösung? Schreib’ hier und du bekommst eine Antwort!