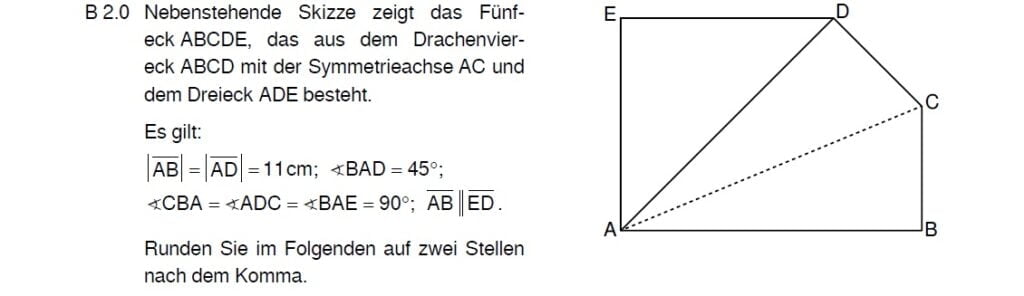

Lösung zu 1.1
Wenn du noch zwei Strecken, aber keinen Winkel mehr hast, verwende deinen Zirkel.
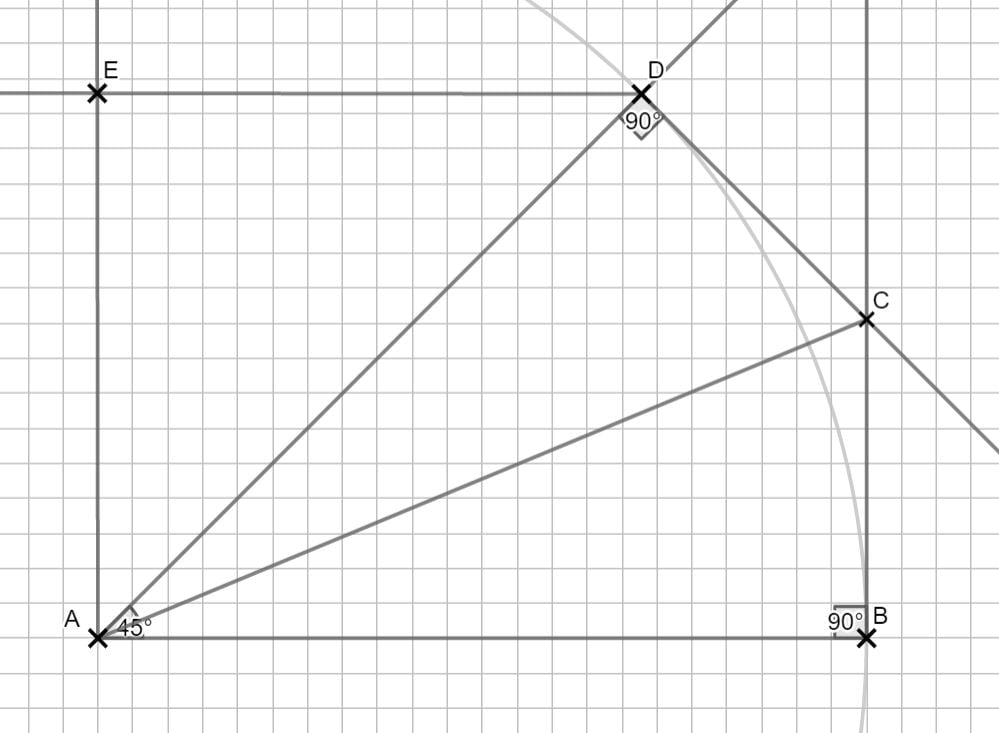
Zurück zum MAP-Hack:

Lösung zu 2.2
Arbeite sauber und begründe jeden Schritt. Was weißt du über Winkel, wenn \( |\overline{AE}| =|\overline{ED}| \) gilt?
\angle DAE &= 45° \, weil \, \angle BAE = 90° \, und \, \angle BAD = 45° \\
\Rightarrow \angle EDA &= 45° \, (\text{Winkelsumme} \triangle ADE) \\
\Rightarrow 90° + 45° & = 135° \\ \triangle & ADE \, ist \,\text{ rechtwinklig-gleichschenklig} \\
\Rightarrow |\overline{AE}| &= |\overline{ED}| \\
Sin(45°) &= \frac{|\overline{ED}|}{11} |\cdot 11 \\ \Rightarrow |\overline{ED}| &= 7,78 cm \end{align} \)
Zurück zum MAP-Hack:

Lösung zu 2.3
Flächenformeln in der Formelsammlung nachschauen und einsetzen. Danach den Anteil vom Ganzen bestimmen und mal 100 rechnen.
tan(0,5 \cdot \angle BAD) &= \frac{|\overline{BC}|}{|\overline{AB}|} \\
tan(22,5°) &= \frac{|\overline{BC}|}{11} |\cdot 11 \, \, \, \Rightarrow |\overline{BC}|= 4,56 cm \\
Fläche_{Drache}: A_1 &= 2 \cdot A_{ABC} \\ &= 2 \cdot (0,5 \cdot |\overline{AB}| \cdot |\overline{BC}|) \\
&= 2 \cdot (0,5 \cdot 11 \cdot 4,56) = 50,16cm^2 \\
\\ Fläche \triangle ADE: A_2 &= 0,5 \cdot |\overline{AE}|\cdot |\overline{ED}| \\
&= 0,5 \cdot 7,78 \cdot 7,78 = 30,26 cm^2 \\ Fünfeck: A_1 + A_2 &= 80,42cm^2 \\
\\ &\text{Berechnung von } p: \\
80,42 cm^2 & \Rightarrow 100 \% \\
50,16 cm^2 & \Rightarrow x \% \\
\\
\Rightarrow \frac{50,16 \cdot 100}{80,42} &= 62,37 \% \end{align} \)
Zurück zum MAP-Hack:

Lösung zu 2.4
Fang von hinten das lesen an. x = 2! Mit dieser Info ist schon vieles leichter.

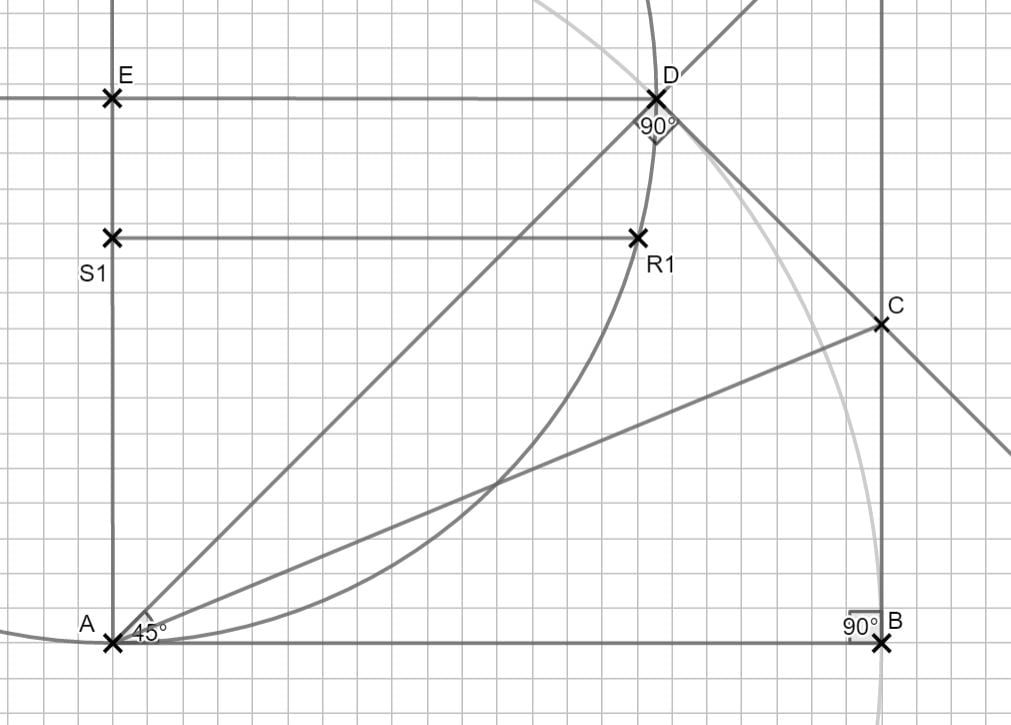
Zurück zum MAP-Hack:

Lösung zu 2.5
An welchen Stellen ist überall der Radius des Kreises? Was wissen wir über ein Dreieck, wenn es zwei gleichlange Seiten hat?
\begin{align} \angle ER_2 A &= \angle DAE + \angle CAD = 45° + 22,5° \text{Symmetrie im Drachen beachten!}\\
\Rightarrow \angle ER_2 A &= 67,5° \\
\triangle & AR_2 E \text{ ist gleischschenklig} \Rightarrow \angle ER_2 A = \angle R_2AE = 67,5° \\
\triangle & AER_2: 180° – 2 \cdot 67,5° = 45° \\
& \text{ Begründung über Ähnlichkeit auch möglich} \\
sin(45°) &= \frac{|\overline{S_2 R_2}|}{|\overline{ER_2}|} \\
sin(45°) &= \frac{|\overline{R_2 S_2}|}{7,78} \, \, | \cdot 7,78 \\
|\overline{R_2 S_2}| &= 5,50cm \end{align}
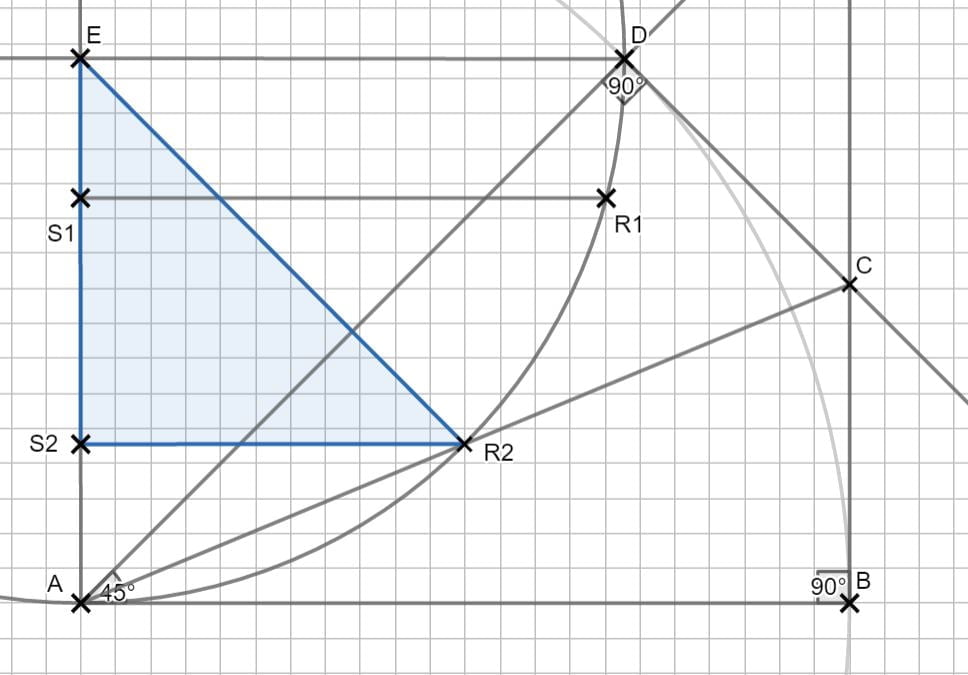
Zurück zum MAP-Hack:

Lösung zu 2.6
Setze in die Formel für die Bogenlänge alles ein, was du kennst. Es bleibt eine Gleichung mit einem x als unbekannte.
\begin{align} b &= \frac{\alpha}{360°} \cdot 2 \cdot r \cdot \pi \\
3 &= \frac{\alpha}{360°} \cdot 2 \cdot 7,78 \cdot \pi \\
\alpha &= 22,09° \\
sin(22,09°) &= \frac{|\overline{ES_3}|}{7,78} \,\, | \cdot 7,78 \\
|\overline{ES_3}| & = 2,93 cm \\
\Rightarrow x &= 2,93 \end{align}

Hallo ,
kann man bei der 2.5 nicht auch den Vierstreckensatz verwenden , weil man ja weiß , dass ED parallel zu S2R2 ist…?
Hallo Selina,
alles was zum richtigen Ergebnis führt, ist (meistens) auch richtig. In den Lösung steht ja, dass da auch was über Ähnlichkeit möglich ist, das deutet ja auch in Richtung VSS. Hast du das richtige Ergebnis raus?
Gerne wieder fragen =)
Tobias Cobanov
Du hast eine Frage zu einer Teilaufgabe oder zur Lösung? Schreib’ hier und du bekommst eine Antwort!